Application of Tensor Neural Networks to Pricing Bermudan Swaptions

The Cheyette model is a quasi-Gaussian volatility interest rate model widely used to price interest rate derivatives such as European and Bermudan Swaptions for which Monte Carlo simulation has become the industry standard. In low dimensions, these approaches provide accurate and robust prices for European Swaptions but, even in this computationally simple setting, they are known to underestimate the value of Bermudan Swaptions when using the state variables as regressors. This is mainly due to the use of a finite number of predetermined basis functions in the regression. Moreover, in high-dimensional settings, these approaches succumb to the Curse of Dimensionality. To address these issues, Deep-learning techniques have been used to solve the backward Stochastic Differential Equation associated with the value process for European and Bermudan Swaptions; however, these methods are constrained by training time and memory. To overcome these limitations, we propose leveraging Tensor Neural Networks as they can provide significant parameter savings while attaining the same accuracy as classical Dense Neural Networks. In this paper we rigorously benchmark the performance of Tensor Neural Networks and Dense Neural Networks for pricing European and Bermudan Swaptions, and we show that Tensor Neural Networks can be trained faster than Dense Neural Networks and provide more accurate and robust prices than their Dense counterparts.

Physics solutions for machine learning privacy leaks

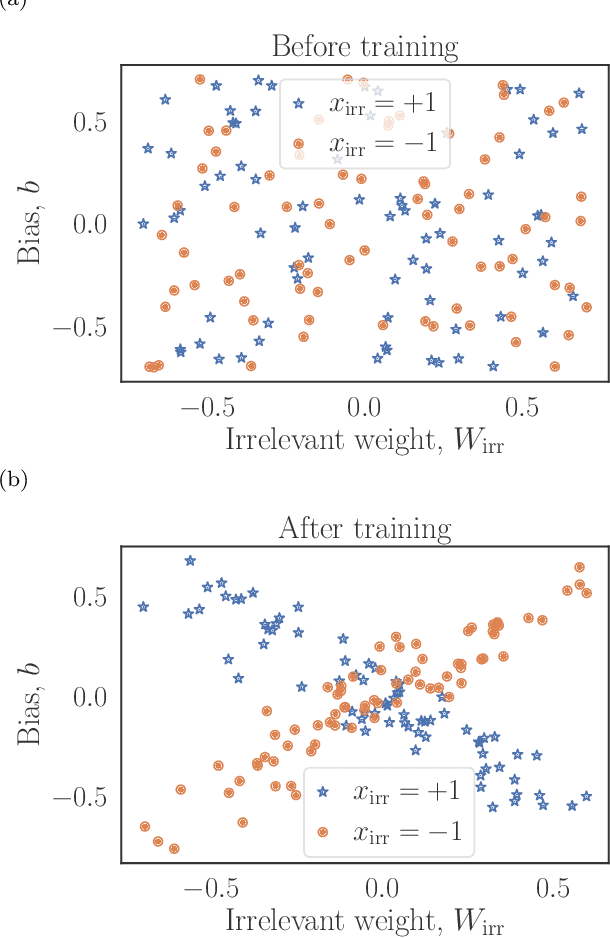
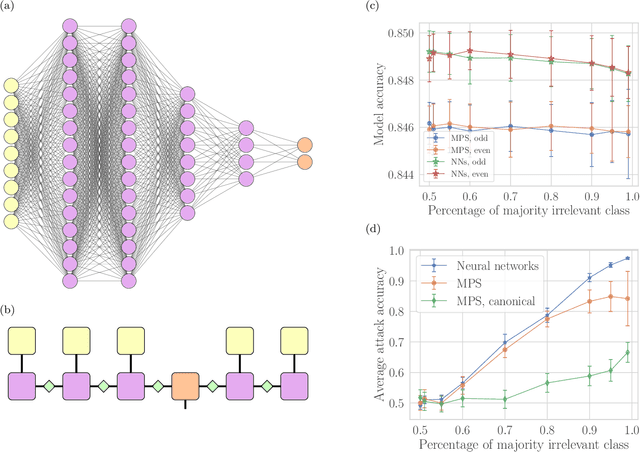
Machine learning systems are becoming more and more ubiquitous in increasingly complex areas, including cutting-edge scientific research. The opposite is also true: the interest in better understanding the inner workings of machine learning systems motivates their analysis under the lens of different scientific disciplines. Physics is particularly successful in this, due to its ability to describe complex dynamical systems. While explanations of phenomena in machine learning based on physics are increasingly present, examples of direct application of notions akin to physics in order to improve machine learning systems are more scarce. Here we provide one such application in the problem of developing algorithms that preserve the privacy of the manipulated data, which is especially important in tasks such as the processing of medical records. We develop well-defined conditions to guarantee robustness to specific types of privacy leaks, and rigorously prove that such conditions are satisfied by tensor-network architectures. These are inspired by the efficient representation of quantum many-body systems, and have shown to compete and even surpass traditional machine learning architectures in certain cases. Given the growing expertise in training tensor-network architectures, these results imply that one may not have to be forced to make a choice between accuracy in prediction and ensuring the privacy of the information processed.