Tensorization of neural networks for improved privacy and interpretability

We present a tensorization algorithm for constructing tensor train representations of functions, drawing on sketching and cross interpolation ideas. The method only requires black-box access to the target function and a small set of sample points defining the domain of interest. Thus, it is particularly well-suited for machine learning models, where the domain of interest is naturally defined by the training dataset. We show that this approach can be used to enhance the privacy and interpretability of neural network models. Specifically, we apply our decomposition to (i) obfuscate neural networks whose parameters encode patterns tied to the training data distribution, and (ii) estimate topological phases of matter that are easily accessible from the tensor train representation. Additionally, we show that this tensorization can serve as an efficient initialization method for optimizing tensor trains in general settings, and that, for model compression, our algorithm achieves a superior trade-off between memory and time complexity compared to conventional tensorization methods of neural networks.

TensorKrowch: Smooth integration of tensor networks in machine learning

Tensor networks are factorizations of high-dimensional tensors into networks of smaller tensors. They have applications in physics and mathematics, and recently have been proposed as promising machine learning architectures. To ease the integration of tensor networks in machine learning pipelines, we introduce TensorKrowch, an open source Python library built on top of PyTorch. Providing a user-friendly interface, TensorKrowch allows users to construct any tensor network, train it, and integrate it as a layer in more intricate deep learning models. In this paper, we describe the main functionality and basic usage of TensorKrowch, and provide technical details on its building blocks and the optimizations performed to achieve efficient operation.

Physics solutions for machine learning privacy leaks

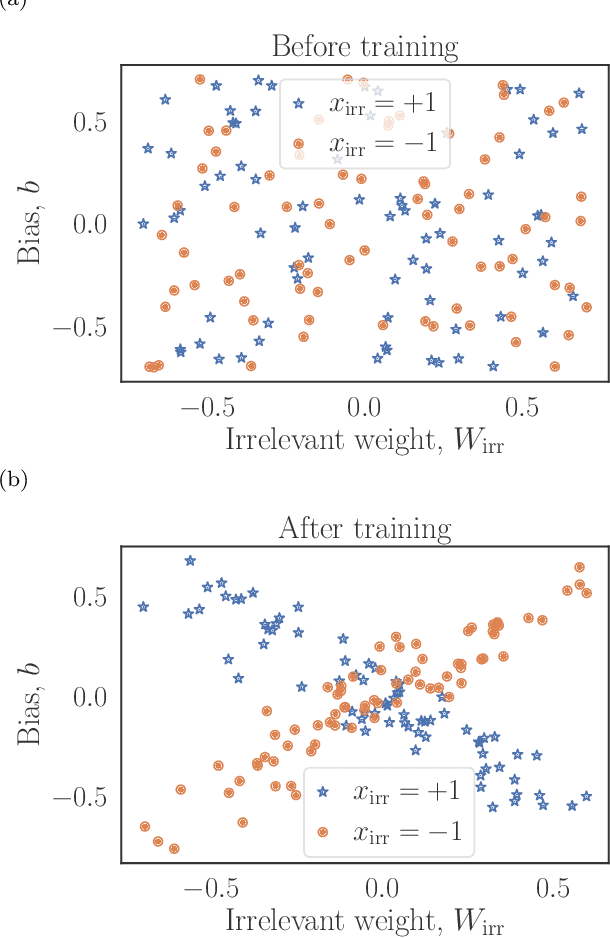
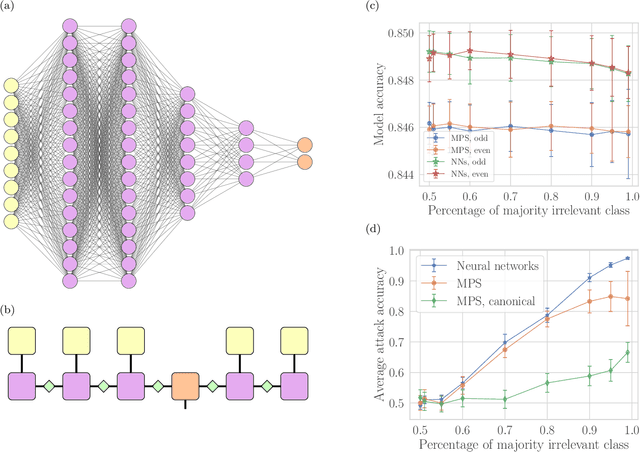
Machine learning systems are becoming more and more ubiquitous in increasingly complex areas, including cutting-edge scientific research. The opposite is also true: the interest in better understanding the inner workings of machine learning systems motivates their analysis under the lens of different scientific disciplines. Physics is particularly successful in this, due to its ability to describe complex dynamical systems. While explanations of phenomena in machine learning based on physics are increasingly present, examples of direct application of notions akin to physics in order to improve machine learning systems are more scarce. Here we provide one such application in the problem of developing algorithms that preserve the privacy of the manipulated data, which is especially important in tasks such as the processing of medical records. We develop well-defined conditions to guarantee robustness to specific types of privacy leaks, and rigorously prove that such conditions are satisfied by tensor-network architectures. These are inspired by the efficient representation of quantum many-body systems, and have shown to compete and even surpass traditional machine learning architectures in certain cases. Given the growing expertise in training tensor-network architectures, these results imply that one may not have to be forced to make a choice between accuracy in prediction and ensuring the privacy of the information processed.