Enhancing reliability in prediction intervals using point forecasters: Heteroscedastic Quantile Regression and Width-Adaptive Conformal Inference

Building prediction intervals for time series forecasting problems presents a complex challenge, particularly when relying solely on point predictors, a common scenario for practitioners in the industry. While research has primarily focused on achieving increasingly efficient valid intervals, we argue that, when evaluating a set of intervals, traditional measures alone are insufficient. There are additional crucial characteristics: the intervals must vary in length, with this variation directly linked to the difficulty of the prediction, and the coverage of the interval must remain independent of the difficulty of the prediction for practical utility. We propose the Heteroscedastic Quantile Regression (HQR) model and the Width-Adaptive Conformal Inference (WACI) method, providing theoretical coverage guarantees, to overcome those issues, respectively. The methodologies are evaluated in the context of Electricity Price Forecasting and Wind Power Forecasting, representing complex scenarios in time series forecasting. The results demonstrate that HQR and WACI not only improve or achieve typical measures of validity and efficiency but also successfully fulfil the commonly ignored mentioned characteristics.

An adaptive standardisation model for Day-Ahead electricity price forecasting

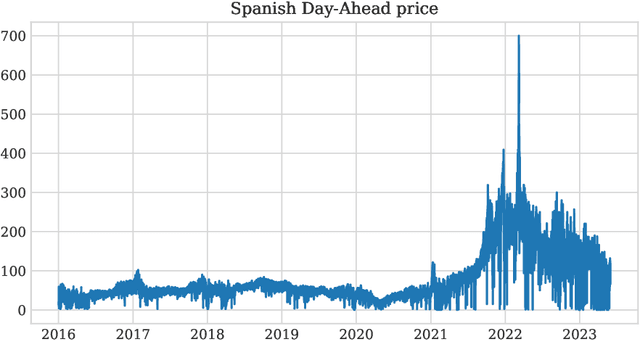
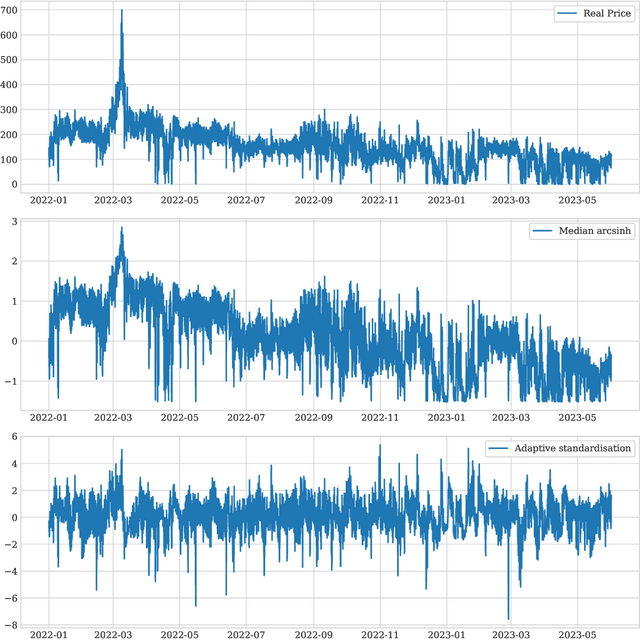
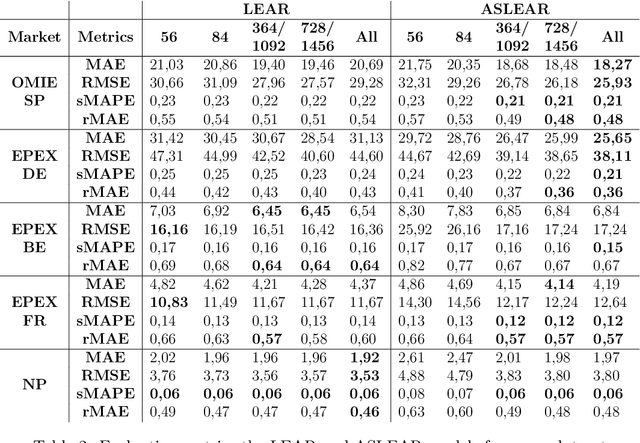
The study of Day-Ahead prices in the electricity market is one of the most popular problems in time series forecasting. Previous research has focused on employing increasingly complex learning algorithms to capture the sophisticated dynamics of the market. However, there is a threshold where increased complexity fails to yield substantial improvements. In this work, we propose an alternative approach by introducing an adaptive standardisation to mitigate the effects of dataset shifts that commonly occur in the market. By doing so, learning algorithms can prioritize uncovering the true relationship between the target variable and the explanatory variables. We investigate four distinct markets, including two novel datasets, previously unexplored in the literature. These datasets provide a more realistic representation of the current market context, that conventional datasets do not show. The results demonstrate a significant improvement across all four markets, using learning algorithms that are less complex yet widely accepted in the literature. This significant advancement unveils opens up new lines of research in this field, highlighting the potential of adaptive transformations in enhancing the performance of forecasting models.

A feature selection method based on Shapley values robust to concept shift in regression

Feature selection is one of the most relevant processes in any methodology for creating a statistical learning model. Generally, existing algorithms establish some criterion to select the most influential variables, discarding those that do not contribute any relevant information to the model. This methodology makes sense in a classical static situation where the joint distribution of the data does not vary over time. However, when dealing with real data, it is common to encounter the problem of the dataset shift and, specifically, changes in the relationships between variables (concept shift). In this case, the influence of a variable cannot be the only indicator of its quality as a regressor of the model, since the relationship learned in the traning phase may not correspond to the current situation. Thus, we propose a new feature selection methodology for regression problems that takes this fact into account, using Shapley values to study the effect that each variable has on the predictions. Five examples are analysed: four correspond to typical situations where the method matches the state of the art and one example related to electricity price forecasting where a concept shift phenomenon has occurred in the Iberian market. In this case the proposed algorithm improves the results significantly.

Physics solutions for machine learning privacy leaks

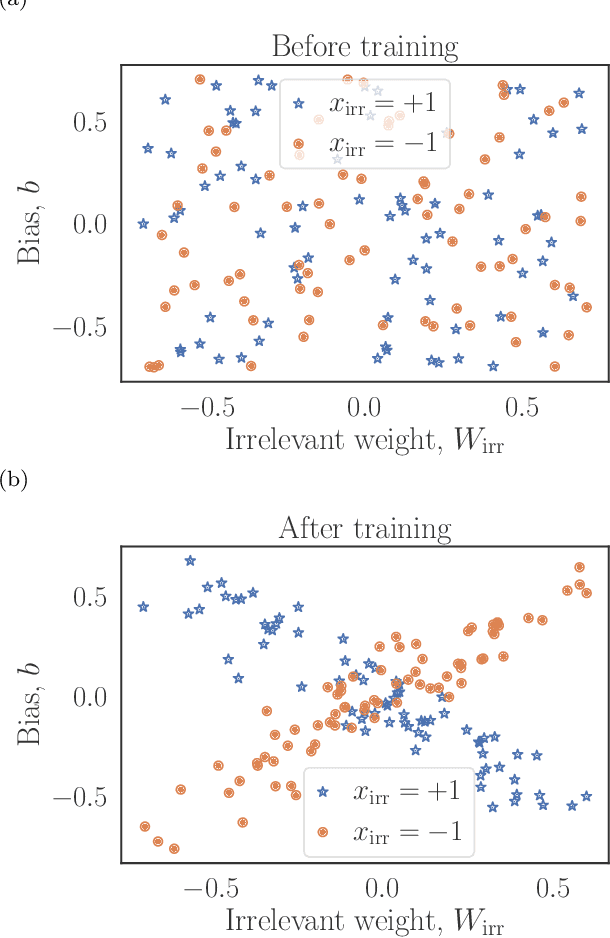
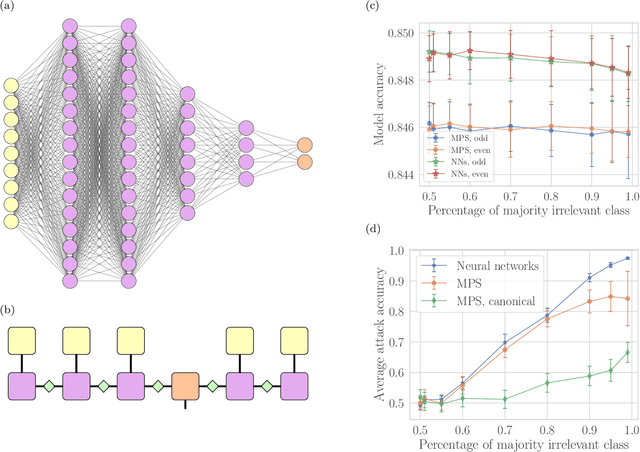
Machine learning systems are becoming more and more ubiquitous in increasingly complex areas, including cutting-edge scientific research. The opposite is also true: the interest in better understanding the inner workings of machine learning systems motivates their analysis under the lens of different scientific disciplines. Physics is particularly successful in this, due to its ability to describe complex dynamical systems. While explanations of phenomena in machine learning based on physics are increasingly present, examples of direct application of notions akin to physics in order to improve machine learning systems are more scarce. Here we provide one such application in the problem of developing algorithms that preserve the privacy of the manipulated data, which is especially important in tasks such as the processing of medical records. We develop well-defined conditions to guarantee robustness to specific types of privacy leaks, and rigorously prove that such conditions are satisfied by tensor-network architectures. These are inspired by the efficient representation of quantum many-body systems, and have shown to compete and even surpass traditional machine learning architectures in certain cases. Given the growing expertise in training tensor-network architectures, these results imply that one may not have to be forced to make a choice between accuracy in prediction and ensuring the privacy of the information processed.