Aggregation in the Mirror Space : Fast, Accurate Distributed Machine Learning in Military Settings

Distributed machine learning (DML) can be an important capability for modern military to take advantage of data and devices distributed at multiple vantage points to adapt and learn. The existing distributed machine learning frameworks, however, cannot realize the full benefits of DML, because they are all based on the simple linear aggregation framework, but linear aggregation cannot handle the $\textit{divergence challenges}$ arising in military settings: the learning data at different devices can be heterogeneous ($\textit{i.e.}$, Non-IID data), leading to model divergence, but the ability for devices to communicate is substantially limited ($\textit{i.e.}$, weak connectivity due to sparse and dynamic communications), reducing the ability for devices to reconcile model divergence. In this paper, we introduce a novel DML framework called aggregation in the mirror space (AIMS) that allows a DML system to introduce a general mirror function to map a model into a mirror space to conduct aggregation and gradient descent. Adapting the convexity of the mirror function according to the divergence force, AIMS allows automatic optimization of DML. We conduct both rigorous analysis and extensive experimental evaluations to demonstrate the benefits of AIMS. For example, we prove that AIMS achieves a loss of $O\left((\frac{m^{r+1}}{T})^{\frac1r}\right)$ after $T$ network-wide updates, where $m$ is the number of devices and $r$ the convexity of the mirror function, with existing linear aggregation frameworks being a special case with $r=2$. Our experimental evaluations using EMANE (Extendable Mobile Ad-hoc Network Emulator) for military communications settings show similar results: AIMS can improve DML convergence rate by up to 57\% and scale well to more devices with weak connectivity, all with little additional computation overhead compared to traditional linear aggregation.

PG3: Policy-Guided Planning for Generalized Policy Generation

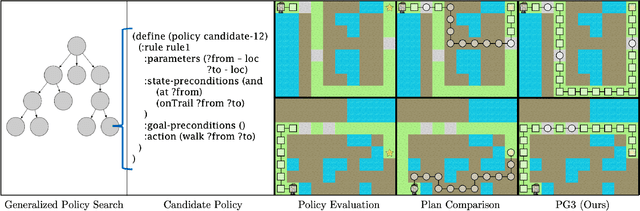
A longstanding objective in classical planning is to synthesize policies that generalize across multiple problems from the same domain. In this work, we study generalized policy search-based methods with a focus on the score function used to guide the search over policies. We demonstrate limitations of two score functions and propose a new approach that overcomes these limitations. The main idea behind our approach, Policy-Guided Planning for Generalized Policy Generation (PG3), is that a candidate policy should be used to guide planning on training problems as a mechanism for evaluating that candidate. Theoretical results in a simplified setting give conditions under which PG3 is optimal or admissible. We then study a specific instantiation of policy search where planning problems are PDDL-based and policies are lifted decision lists. Empirical results in six domains confirm that PG3 learns generalized policies more efficiently and effectively than several baselines. Code: https://github.com/ryangpeixu/pg3

Achieving Efficient Distributed Machine Learning Using a Novel Non-Linear Class of Aggregation Functions

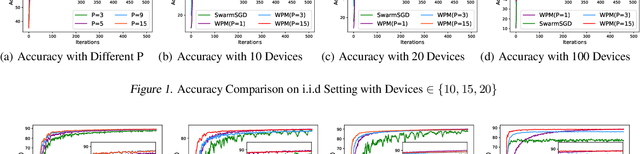
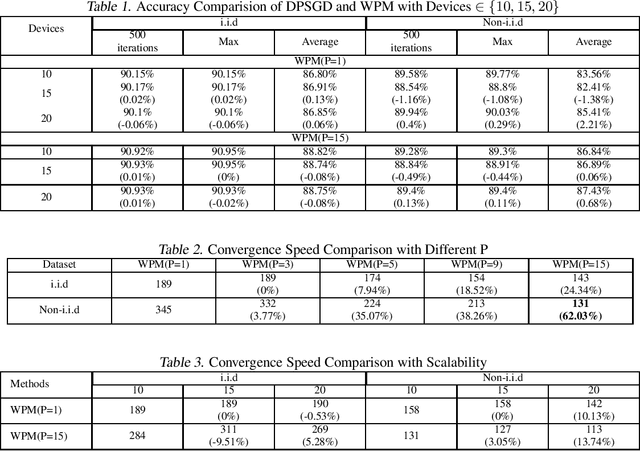
Distributed machine learning (DML) over time-varying networks can be an enabler for emerging decentralized ML applications such as autonomous driving and drone fleeting. However, the commonly used weighted arithmetic mean model aggregation function in existing DML systems can result in high model loss, low model accuracy, and slow convergence speed over time-varying networks. To address this issue, in this paper, we propose a novel non-linear class of model aggregation functions to achieve efficient DML over time-varying networks. Instead of taking a linear aggregation of neighboring models as most existing studies do, our mechanism uses a nonlinear aggregation, a weighted power-p mean (WPM) where p is a positive odd integer, as the aggregation function of local models from neighbors. The subsequent optimizing steps are taken using mirror descent defined by a Bregman divergence that maintains convergence to optimality. In this paper, we analyze properties of the WPM and rigorously prove convergence properties of our aggregation mechanism. Additionally, through extensive experiments, we show that when p > 1, our design significantly improves the convergence speed of the model and the scalability of DML under time-varying networks compared with arithmetic mean aggregation functions, with little additional 26computation overhead.