Achieving Efficient Distributed Machine Learning Using a Novel Non-Linear Class of Aggregation Functions
Paper and Code
Jan 29, 2022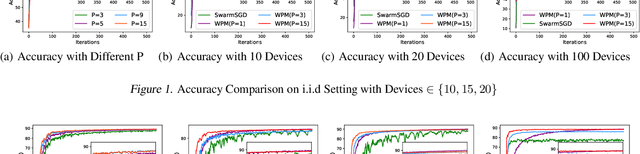
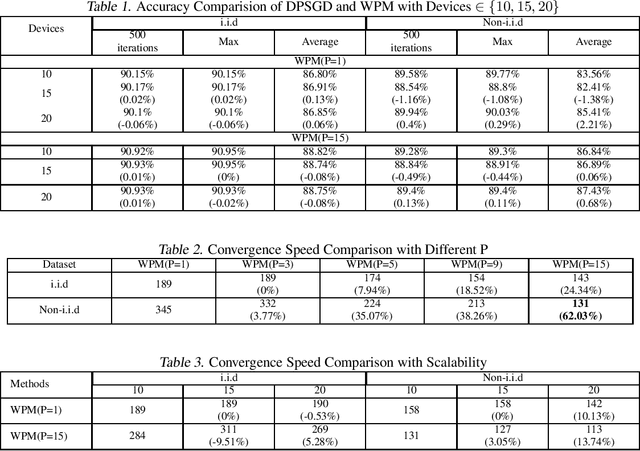


Distributed machine learning (DML) over time-varying networks can be an enabler for emerging decentralized ML applications such as autonomous driving and drone fleeting. However, the commonly used weighted arithmetic mean model aggregation function in existing DML systems can result in high model loss, low model accuracy, and slow convergence speed over time-varying networks. To address this issue, in this paper, we propose a novel non-linear class of model aggregation functions to achieve efficient DML over time-varying networks. Instead of taking a linear aggregation of neighboring models as most existing studies do, our mechanism uses a nonlinear aggregation, a weighted power-p mean (WPM) where p is a positive odd integer, as the aggregation function of local models from neighbors. The subsequent optimizing steps are taken using mirror descent defined by a Bregman divergence that maintains convergence to optimality. In this paper, we analyze properties of the WPM and rigorously prove convergence properties of our aggregation mechanism. Additionally, through extensive experiments, we show that when p > 1, our design significantly improves the convergence speed of the model and the scalability of DML under time-varying networks compared with arithmetic mean aggregation functions, with little additional 26computation overhead.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge