Fairness in Federated Learning via Core-Stability

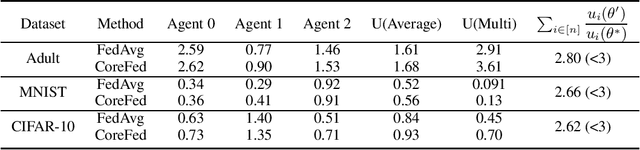
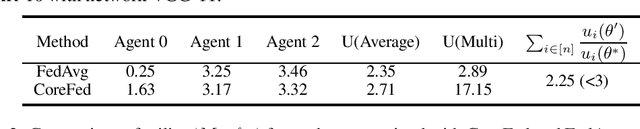
Federated learning provides an effective paradigm to jointly optimize a model benefited from rich distributed data while protecting data privacy. Nonetheless, the heterogeneity nature of distributed data makes it challenging to define and ensure fairness among local agents. For instance, it is intuitively "unfair" for agents with data of high quality to sacrifice their performance due to other agents with low quality data. Currently popular egalitarian and weighted equity-based fairness measures suffer from the aforementioned pitfall. In this work, we aim to formally represent this problem and address these fairness issues using concepts from co-operative game theory and social choice theory. We model the task of learning a shared predictor in the federated setting as a fair public decision making problem, and then define the notion of core-stable fairness: Given $N$ agents, there is no subset of agents $S$ that can benefit significantly by forming a coalition among themselves based on their utilities $U_N$ and $U_S$ (i.e., $\frac{|S|}{N} U_S \geq U_N$). Core-stable predictors are robust to low quality local data from some agents, and additionally they satisfy Proportionality and Pareto-optimality, two well sought-after fairness and efficiency notions within social choice. We then propose an efficient federated learning protocol CoreFed to optimize a core stable predictor. CoreFed determines a core-stable predictor when the loss functions of the agents are convex. CoreFed also determines approximate core-stable predictors when the loss functions are not convex, like smooth neural networks. We further show the existence of core-stable predictors in more general settings using Kakutani's fixed point theorem. Finally, we empirically validate our analysis on two real-world datasets, and we show that CoreFed achieves higher core-stability fairness than FedAvg while having similar accuracy.

(Almost) Envy-Free, Proportional and Efficient Allocations of an Indivisible Mixed Manna

We study the problem of finding fair and efficient allocations of a set of indivisible items to a set of agents, where each item may be a good (positively valued) for some agents and a bad (negatively valued) for others, i.e., a mixed manna. As fairness notions, we consider arguably the strongest possible relaxations of envy-freeness and proportionality, namely envy-free up to any item (EFX and EFX$_0$), and proportional up to the maximin good or any bad (PropMX and PropMX$_0$). Our efficiency notion is Pareto-optimality (PO). We study two types of instances: (i) Separable, where the item set can be partitioned into goods and bads, and (ii) Restricted mixed goods (RMG), where for each item $j$, every agent has either a non-positive value for $j$, or values $j$ at the same $v_j>0$. We obtain polynomial-time algorithms for the following: (i) Separable instances: PropMX$_0$ allocation. (ii) RMG instances: Let pure bads be the set of items that everyone values negatively. - PropMX allocation for general pure bads. - EFX+PropMX allocation for identically-ordered pure bads. - EFX+PropMX+PO allocation for identical pure bads. Finally, if the RMG instances are further restricted to binary mixed goods where all the $v_j$'s are the same, we strengthen the results to guarantee EFX$_0$ and PropMX$_0$ respectively.

Social welfare and profit maximization from revealed preferences

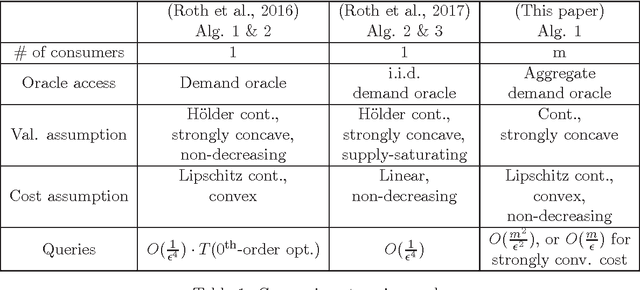
Consider the seller's problem of finding optimal prices for her $n$ (divisible) goods when faced with a set of $m$ consumers, given that she can only observe their purchased bundles at posted prices, i.e., revealed preferences. We study both social welfare and profit maximization with revealed preferences. Although social welfare maximization is a seemingly non-convex optimization problem in prices, we show that (i) it can be reduced to a dual convex optimization problem in prices, and (ii) the revealed preferences can be interpreted as supergradients of the concave conjugate of valuation, with which subgradients of the dual function can be computed. We thereby obtain a simple subgradient-based algorithm for strongly concave valuations and convex cost, with query complexity $O(m^2/\epsilon^2)$, where $\epsilon$ is the additive difference between the social welfare induced by our algorithm and the optimum social welfare. We also study social welfare maximization under the online setting, specifically the random permutation model, where consumers arrive one-by-one in a random order. For the case where consumer valuations can be arbitrary continuous functions, we propose a price posting mechanism that achieves an expected social welfare up to an additive factor of $O(\sqrt{mn})$ from the maximum social welfare. Finally, for profit maximization (which may be non-convex in simple cases), we give nearly matching upper and lower bounds on the query complexity for separable valuations and cost (i.e., each good can be treated independently).

Eliciting Binary Performance Metrics

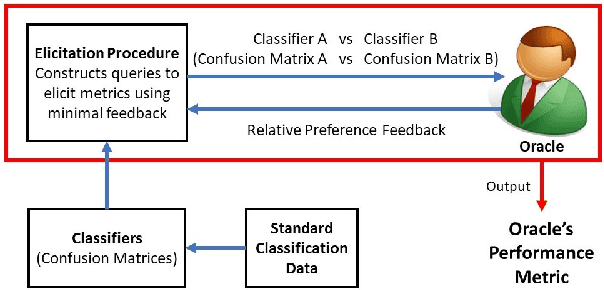
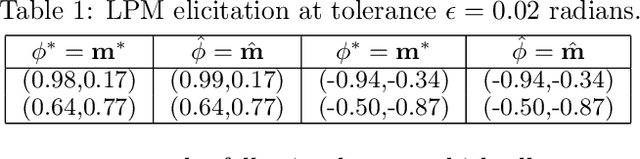
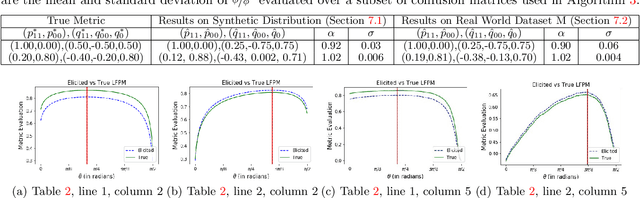
Given a binary prediction problem, which performance metric should the classifier optimize? We address this question by formalizing the problem of metric elicitation. In particular, we focus on eliciting binary performance metrics from pairwise preferences, where users provide relative feedback for pairs of classifiers. By exploiting key properties of the space of confusion matrices, we obtain provably query efficient algorithms for eliciting linear and linear-fractional metrics. We further show that our method is robust to feedback and finite sample noise.

Learning Economic Parameters from Revealed Preferences

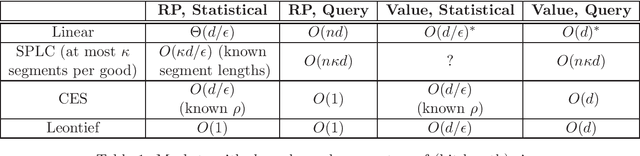
A recent line of work, starting with Beigman and Vohra (2006) and Zadimoghaddam and Roth (2012), has addressed the problem of {\em learning} a utility function from revealed preference data. The goal here is to make use of past data describing the purchases of a utility maximizing agent when faced with certain prices and budget constraints in order to produce a hypothesis function that can accurately forecast the {\em future} behavior of the agent. In this work we advance this line of work by providing sample complexity guarantees and efficient algorithms for a number of important classes. By drawing a connection to recent advances in multi-class learning, we provide a computationally efficient algorithm with tight sample complexity guarantees ($\Theta(d/\epsilon)$ for the case of $d$ goods) for learning linear utility functions under a linear price model. This solves an open question in Zadimoghaddam and Roth (2012). Our technique yields numerous generalizations including the ability to learn other well-studied classes of utility functions, to deal with a misspecified model, and with non-linear prices.