Social welfare and profit maximization from revealed preferences
Paper and Code
Oct 06, 2018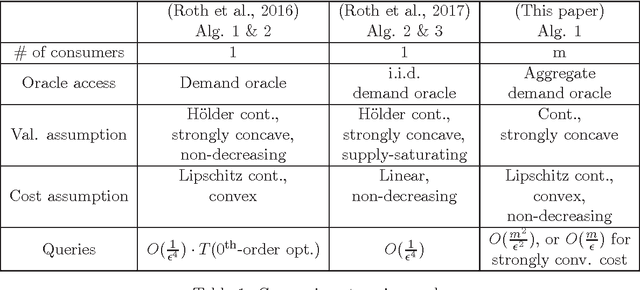
Consider the seller's problem of finding optimal prices for her $n$ (divisible) goods when faced with a set of $m$ consumers, given that she can only observe their purchased bundles at posted prices, i.e., revealed preferences. We study both social welfare and profit maximization with revealed preferences. Although social welfare maximization is a seemingly non-convex optimization problem in prices, we show that (i) it can be reduced to a dual convex optimization problem in prices, and (ii) the revealed preferences can be interpreted as supergradients of the concave conjugate of valuation, with which subgradients of the dual function can be computed. We thereby obtain a simple subgradient-based algorithm for strongly concave valuations and convex cost, with query complexity $O(m^2/\epsilon^2)$, where $\epsilon$ is the additive difference between the social welfare induced by our algorithm and the optimum social welfare. We also study social welfare maximization under the online setting, specifically the random permutation model, where consumers arrive one-by-one in a random order. For the case where consumer valuations can be arbitrary continuous functions, we propose a price posting mechanism that achieves an expected social welfare up to an additive factor of $O(\sqrt{mn})$ from the maximum social welfare. Finally, for profit maximization (which may be non-convex in simple cases), we give nearly matching upper and lower bounds on the query complexity for separable valuations and cost (i.e., each good can be treated independently).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge