Vijay V. Vazirani
Learning Economic Parameters from Revealed Preferences
Jul 30, 2014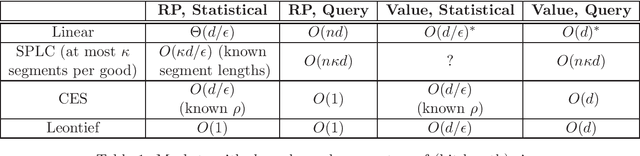
Abstract:A recent line of work, starting with Beigman and Vohra (2006) and Zadimoghaddam and Roth (2012), has addressed the problem of {\em learning} a utility function from revealed preference data. The goal here is to make use of past data describing the purchases of a utility maximizing agent when faced with certain prices and budget constraints in order to produce a hypothesis function that can accurately forecast the {\em future} behavior of the agent. In this work we advance this line of work by providing sample complexity guarantees and efficient algorithms for a number of important classes. By drawing a connection to recent advances in multi-class learning, we provide a computationally efficient algorithm with tight sample complexity guarantees ($\Theta(d/\epsilon)$ for the case of $d$ goods) for learning linear utility functions under a linear price model. This solves an open question in Zadimoghaddam and Roth (2012). Our technique yields numerous generalizations including the ability to learn other well-studied classes of utility functions, to deal with a misspecified model, and with non-linear prices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge