Weakly Supervised Monocular 3D Object Detection using Multi-View Projection and Direction Consistency

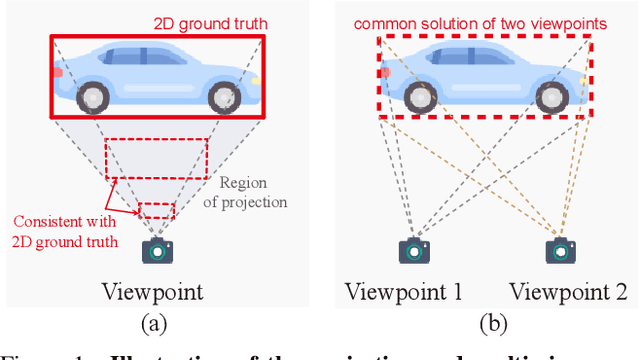
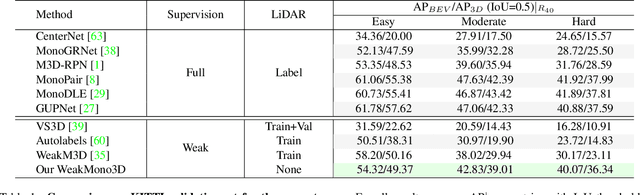
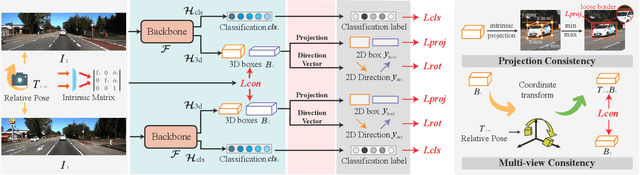
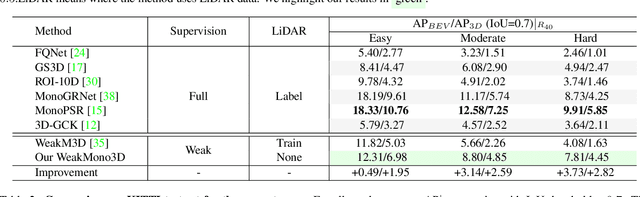
Monocular 3D object detection has become a mainstream approach in automatic driving for its easy application. A prominent advantage is that it does not need LiDAR point clouds during the inference. However, most current methods still rely on 3D point cloud data for labeling the ground truths used in the training phase. This inconsistency between the training and inference makes it hard to utilize the large-scale feedback data and increases the data collection expenses. To bridge this gap, we propose a new weakly supervised monocular 3D objection detection method, which can train the model with only 2D labels marked on images. To be specific, we explore three types of consistency in this task, i.e. the projection, multi-view and direction consistency, and design a weakly-supervised architecture based on these consistencies. Moreover, we propose a new 2D direction labeling method in this task to guide the model for accurate rotation direction prediction. Experiments show that our weakly-supervised method achieves comparable performance with some fully supervised methods. When used as a pre-training method, our model can significantly outperform the corresponding fully-supervised baseline with only 1/3 3D labels. https://github.com/weakmono3d/weakmono3d

A Convergence Theory for Federated Average: Beyond Smoothness

Federated learning enables a large amount of edge computing devices to learn a model without data sharing jointly. As a leading algorithm in this setting, Federated Average FedAvg, which runs Stochastic Gradient Descent (SGD) in parallel on local devices and averages the sequences only once in a while, have been widely used due to their simplicity and low communication cost. However, despite recent research efforts, it lacks theoretical analysis under assumptions beyond smoothness. In this paper, we analyze the convergence of FedAvg. Different from the existing work, we relax the assumption of strong smoothness. More specifically, we assume the semi-smoothness and semi-Lipschitz properties for the loss function, which have an additional first-order term in assumption definitions. In addition, we also assume bound on the gradient, which is weaker than the commonly used bounded gradient assumption in the convergence analysis scheme. As a solution, this paper provides a theoretical convergence study on Federated Learning.

Sublinear Time Algorithm for Online Weighted Bipartite Matching

Online bipartite matching is a fundamental problem in online algorithms. The goal is to match two sets of vertices to maximize the sum of the edge weights, where for one set of vertices, each vertex and its corresponding edge weights appear in a sequence. Currently, in the practical recommendation system or search engine, the weights are decided by the inner product between the deep representation of a user and the deep representation of an item. The standard online matching needs to pay $nd$ time to linear scan all the $n$ items, computing weight (assuming each representation vector has length $d$), and then decide the matching based on the weights. However, in reality, the $n$ could be very large, e.g. in online e-commerce platforms. Thus, improving the time of computing weights is a problem of practical significance. In this work, we provide the theoretical foundation for computing the weights approximately. We show that, with our proposed randomized data structures, the weights can be computed in sublinear time while still preserving the competitive ratio of the matching algorithm.

Symmetric Boolean Factor Analysis with Applications to InstaHide

In this work we examine the security of InstaHide, a recently proposed scheme for distributed learning (Huang et al.). A number of recent works have given reconstruction attacks for InstaHide in various regimes by leveraging an intriguing connection to the following matrix factorization problem: given the Gram matrix of a collection of m random k-sparse Boolean vectors in {0,1}^r, recover the vectors (up to the trivial symmetries). Equivalently, this can be thought of as a sparse, symmetric variant of the well-studied problem of Boolean factor analysis, or as an average-case version of the classic problem of recovering a k-uniform hypergraph from its line graph. As previous algorithms either required m to be exponentially large in k or only applied to k = 2, they left open the question of whether InstaHide possesses some form of "fine-grained security" against reconstruction attacks for moderately large k. In this work, we answer this in the negative by giving a simple O(m^{\omega + 1}) time algorithm for the above matrix factorization problem. Our algorithm, based on tensor decomposition, only requires m to be at least quasi-linear in r. We complement this result with a quasipolynomial-time algorithm for a worst-case setting of the problem where the collection of k-sparse vectors is chosen arbitrarily.

InstaHide's Sample Complexity When Mixing Two Private Images

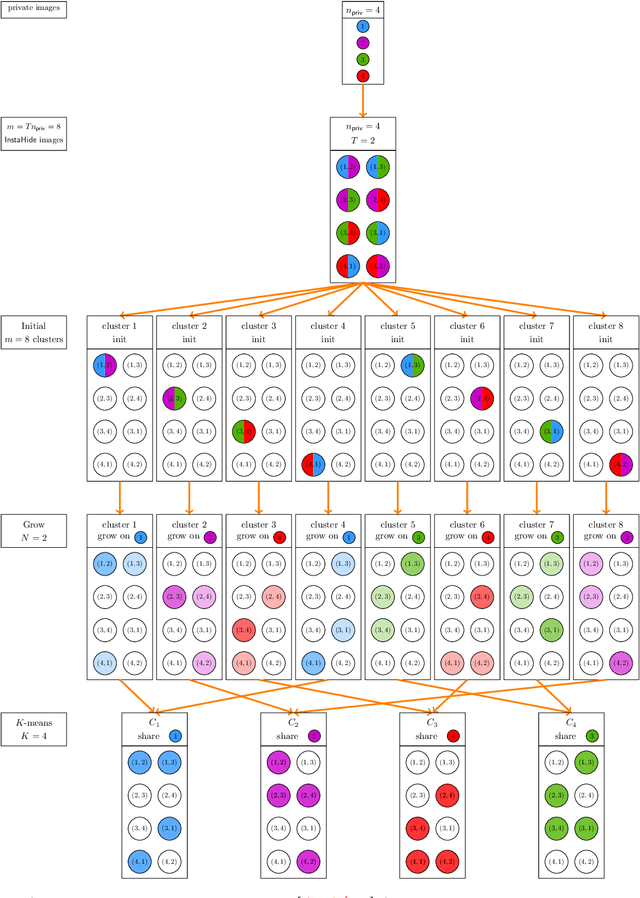
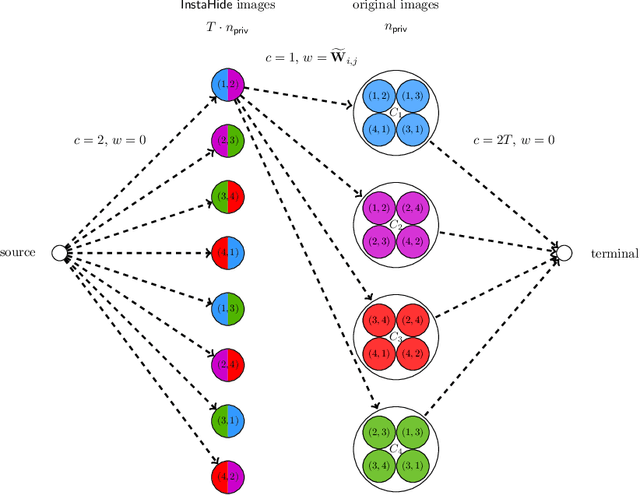
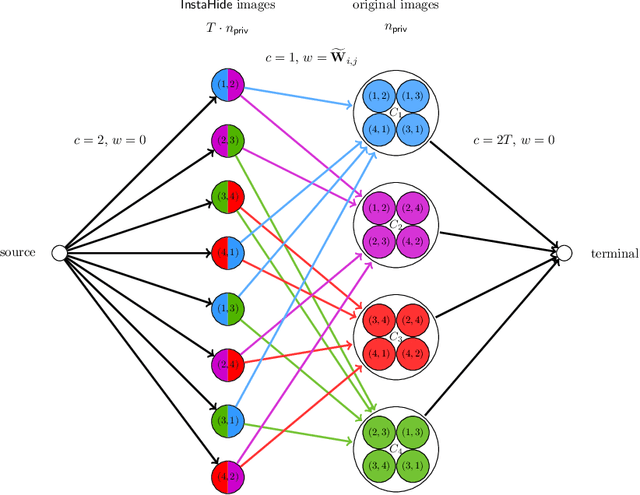
Inspired by InstaHide challenge [Huang, Song, Li and Arora'20], [Chen, Song and Zhuo'20] recently provides one mathematical formulation of InstaHide attack problem under Gaussian images distribution. They show that it suffices to use $O(n_{\mathsf{priv}}^{k_{\mathsf{priv}} - 2/(k_{\mathsf{priv}} + 1)})$ samples to recover one private image in $n_{\mathsf{priv}}^{O(k_{\mathsf{priv}})} + \mathrm{poly}(n_{\mathsf{pub}})$ time for any integer $k_{\mathsf{priv}}$, where $n_{\mathsf{priv}}$ and $n_{\mathsf{pub}}$ denote the number of images used in the private and the public dataset to generate a mixed image sample. Under the current setup for the InstaHide challenge of mixing two private images ($k_{\mathsf{priv}} = 2$), this means $n_{\mathsf{priv}}^{4/3}$ samples are sufficient to recover a private image. In this work, we show that $n_{\mathsf{priv}} \log ( n_{\mathsf{priv}} )$ samples are sufficient (information-theoretically) for recovering all the private images.