InstaHide's Sample Complexity When Mixing Two Private Images
Paper and Code
Nov 24, 2020
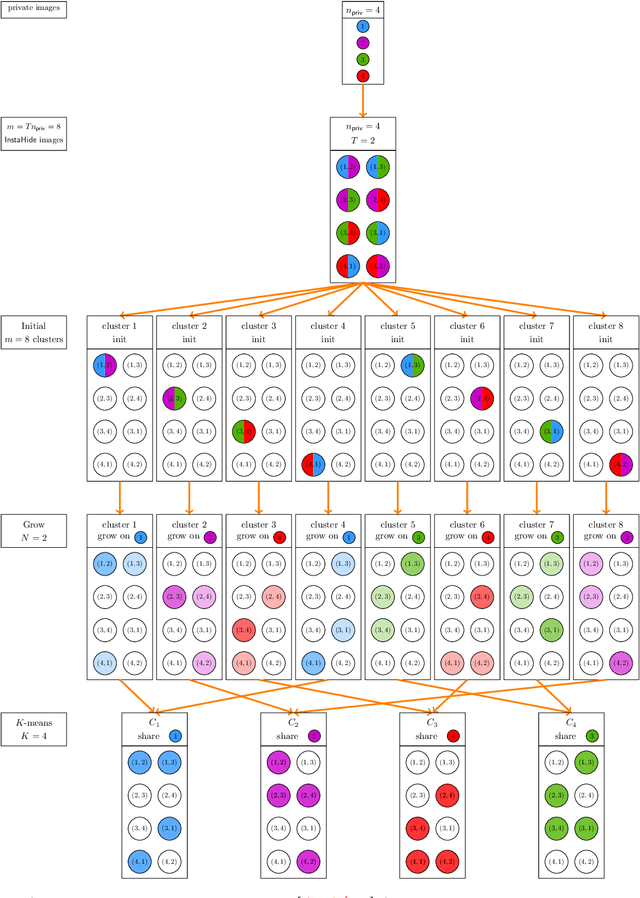
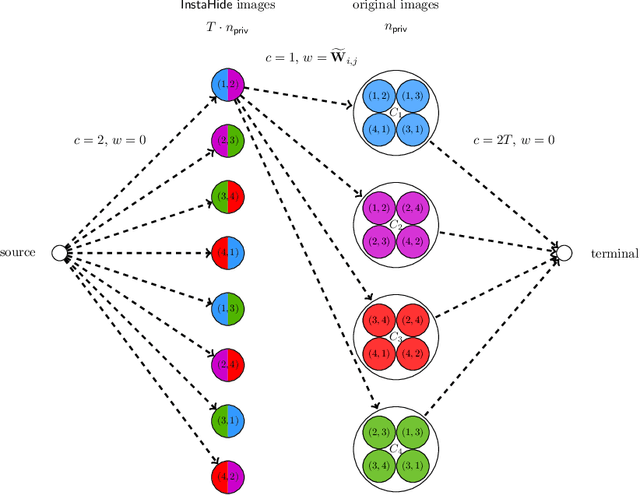
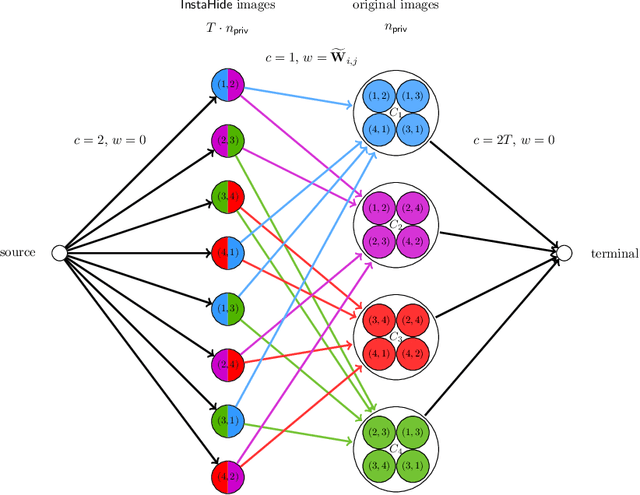
Inspired by InstaHide challenge [Huang, Song, Li and Arora'20], [Chen, Song and Zhuo'20] recently provides one mathematical formulation of InstaHide attack problem under Gaussian images distribution. They show that it suffices to use $O(n_{\mathsf{priv}}^{k_{\mathsf{priv}} - 2/(k_{\mathsf{priv}} + 1)})$ samples to recover one private image in $n_{\mathsf{priv}}^{O(k_{\mathsf{priv}})} + \mathrm{poly}(n_{\mathsf{pub}})$ time for any integer $k_{\mathsf{priv}}$, where $n_{\mathsf{priv}}$ and $n_{\mathsf{pub}}$ denote the number of images used in the private and the public dataset to generate a mixed image sample. Under the current setup for the InstaHide challenge of mixing two private images ($k_{\mathsf{priv}} = 2$), this means $n_{\mathsf{priv}}^{4/3}$ samples are sufficient to recover a private image. In this work, we show that $n_{\mathsf{priv}} \log ( n_{\mathsf{priv}} )$ samples are sufficient (information-theoretically) for recovering all the private images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge