The MiniMax-M2 Series: Mini Activations Unleashing Max Real-World Intelligence

We introduce the MiniMax-M2 series, a family of Mixture-of-Experts language models built around the principle that mini activations can unleash maximum real-world intelligence. The flagship M2 contains 229.9B total parameters with only 9.8B activated per token. Designed end-to-end for agentic deployment, the M2 series rests on three components: (i) agent-driven data pipelines producing large-scale, verifiable trajectories across agentic coding and agentic cowork, each grounded in an executable workspace and an artifact-aligned reward; (ii) Forge, a scalable agent-native RL system that adapts to long-horizon agent trajectories, paired with windowed-FIFO scheduling, prefix-tree merging, inference optimization, and a clean training-inference-agent decoupling that supports both white-box and black-box agents; (iii) the latest M2.7 checkpoint takes an early step toward self-evolution -- autonomously debugging training runs and modifying its own scaffold. Across M2 through M2.7, this combination translates a mini-activation footprint into frontier-tier performance on agentic coding, deep search, office-task, and reasoning benchmarks.

MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention

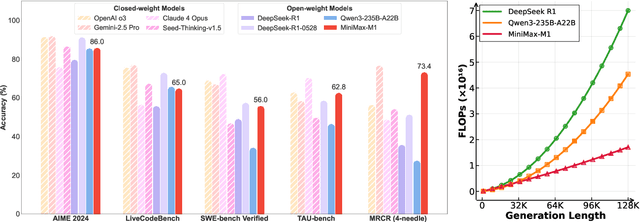
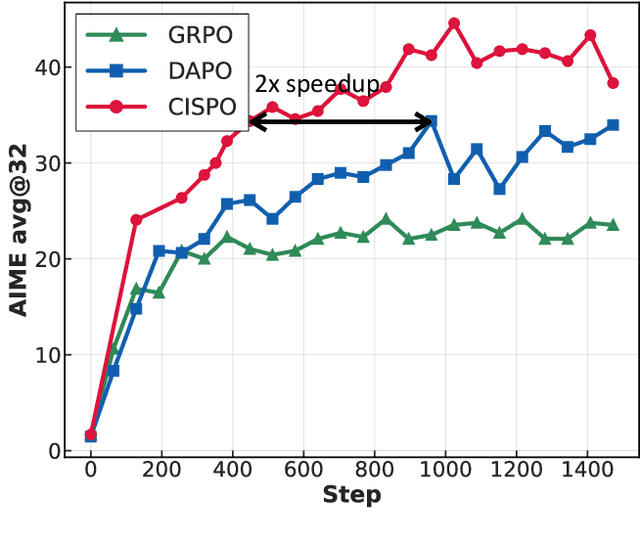
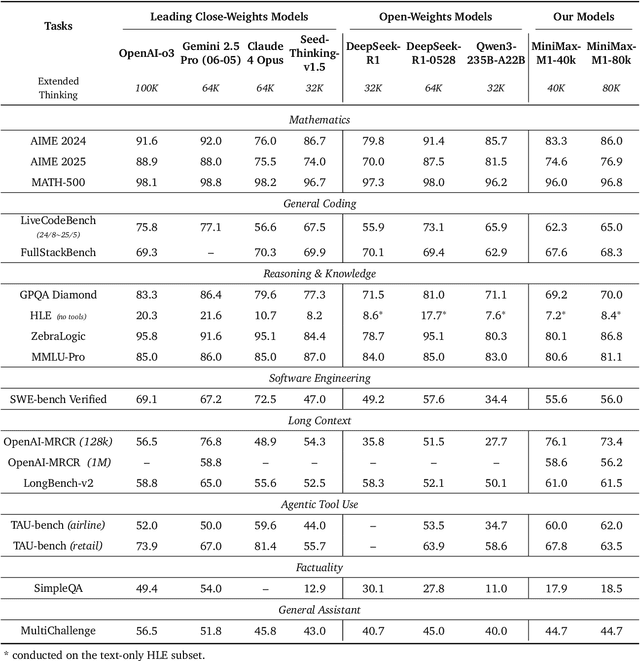
We introduce MiniMax-M1, the world's first open-weight, large-scale hybrid-attention reasoning model. MiniMax-M1 is powered by a hybrid Mixture-of-Experts (MoE) architecture combined with a lightning attention mechanism. The model is developed based on our previous MiniMax-Text-01 model, which contains a total of 456 billion parameters with 45.9 billion parameters activated per token. The M1 model natively supports a context length of 1 million tokens, 8x the context size of DeepSeek R1. Furthermore, the lightning attention mechanism in MiniMax-M1 enables efficient scaling of test-time compute. These properties make M1 particularly suitable for complex tasks that require processing long inputs and thinking extensively. MiniMax-M1 is trained using large-scale reinforcement learning (RL) on diverse problems including sandbox-based, real-world software engineering environments. In addition to M1's inherent efficiency advantage for RL training, we propose CISPO, a novel RL algorithm to further enhance RL efficiency. CISPO clips importance sampling weights rather than token updates, outperforming other competitive RL variants. Combining hybrid-attention and CISPO enables MiniMax-M1's full RL training on 512 H800 GPUs to complete in only three weeks, with a rental cost of just $534,700. We release two versions of MiniMax-M1 models with 40K and 80K thinking budgets respectively, where the 40K model represents an intermediate phase of the 80K training. Experiments on standard benchmarks show that our models are comparable or superior to strong open-weight models such as the original DeepSeek-R1 and Qwen3-235B, with particular strengths in complex software engineering, tool utilization, and long-context tasks. We publicly release MiniMax-M1 at https://github.com/MiniMax-AI/MiniMax-M1.

MiniMax-01: Scaling Foundation Models with Lightning Attention

We introduce MiniMax-01 series, including MiniMax-Text-01 and MiniMax-VL-01, which are comparable to top-tier models while offering superior capabilities in processing longer contexts. The core lies in lightning attention and its efficient scaling. To maximize computational capacity, we integrate it with Mixture of Experts (MoE), creating a model with 32 experts and 456 billion total parameters, of which 45.9 billion are activated for each token. We develop an optimized parallel strategy and highly efficient computation-communication overlap techniques for MoE and lightning attention. This approach enables us to conduct efficient training and inference on models with hundreds of billions of parameters across contexts spanning millions of tokens. The context window of MiniMax-Text-01 can reach up to 1 million tokens during training and extrapolate to 4 million tokens during inference at an affordable cost. Our vision-language model, MiniMax-VL-01 is built through continued training with 512 billion vision-language tokens. Experiments on both standard and in-house benchmarks show that our models match the performance of state-of-the-art models like GPT-4o and Claude-3.5-Sonnet while offering 20-32 times longer context window. We publicly release MiniMax-01 at https://github.com/MiniMax-AI.

Scaling Laws for Linear Complexity Language Models

The interest in linear complexity models for large language models is on the rise, although their scaling capacity remains uncertain. In this study, we present the scaling laws for linear complexity language models to establish a foundation for their scalability. Specifically, we examine the scaling behaviors of three efficient linear architectures. These include TNL, a linear attention model with data-independent decay; HGRN2, a linear RNN with data-dependent decay; and cosFormer2, a linear attention model without decay. We also include LLaMA as a baseline architecture for softmax attention for comparison. These models were trained with six variants, ranging from 70M to 7B parameters on a 300B-token corpus, and evaluated with a total of 1,376 intermediate checkpoints on various downstream tasks. These tasks include validation loss, commonsense reasoning, and information retrieval and generation. The study reveals that existing linear complexity language models exhibit similar scaling capabilities as conventional transformer-based models while also demonstrating superior linguistic proficiency and knowledge retention.

CircNet: Meshing 3D Point Clouds with Circumcenter Detection

Reconstructing 3D point clouds into triangle meshes is a key problem in computational geometry and surface reconstruction. Point cloud triangulation solves this problem by providing edge information to the input points. Since no vertex interpolation is involved, it is beneficial to preserve sharp details on the surface. Taking advantage of learning-based techniques in triangulation, existing methods enumerate the complete combinations of candidate triangles, which is both complex and inefficient. In this paper, we leverage the duality between a triangle and its circumcenter, and introduce a deep neural network that detects the circumcenters to achieve point cloud triangulation. Specifically, we introduce multiple anchor priors to divide the neighborhood space of each point. The neural network then learns to predict the presences and locations of circumcenters under the guidance of those anchors. We extract the triangles dual to the detected circumcenters to form a primitive mesh, from which an edge-manifold mesh is produced via simple post-processing. Unlike existing learning-based triangulation methods, the proposed method bypasses an exhaustive enumeration of triangle combinations and local surface parameterization. We validate the efficiency, generalization, and robustness of our method on prominent datasets of both watertight and open surfaces. The code and trained models are provided at https://github.com/Ruitao-L/CircNet.