Kov: Transferable and Naturalistic Black-Box LLM Attacks using Markov Decision Processes and Tree Search

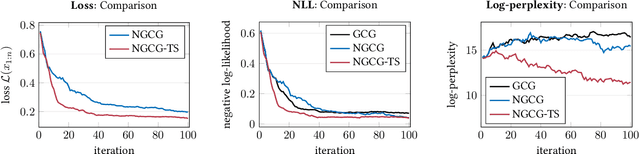
Eliciting harmful behavior from large language models (LLMs) is an important task to ensure the proper alignment and safety of the models. Often when training LLMs, ethical guidelines are followed yet alignment failures may still be uncovered through red teaming adversarial attacks. This work frames the red-teaming problem as a Markov decision process (MDP) and uses Monte Carlo tree search to find harmful behaviors of black-box, closed-source LLMs. We optimize token-level prompt suffixes towards targeted harmful behaviors on white-box LLMs and include a naturalistic loss term, log-perplexity, to generate more natural language attacks for better interpretability. The proposed algorithm, Kov, trains on white-box LLMs to optimize the adversarial attacks and periodically evaluates responses from the black-box LLM to guide the search towards more harmful black-box behaviors. In our preliminary study, results indicate that we can jailbreak black-box models, such as GPT-3.5, in only 10 queries, yet fail on GPT-4$-$which may indicate that newer models are more robust to token-level attacks. All work to reproduce these results is open sourced (https://github.com/sisl/Kov.jl).

ConstrainedZero: Chance-Constrained POMDP Planning using Learned Probabilistic Failure Surrogates and Adaptive Safety Constraints

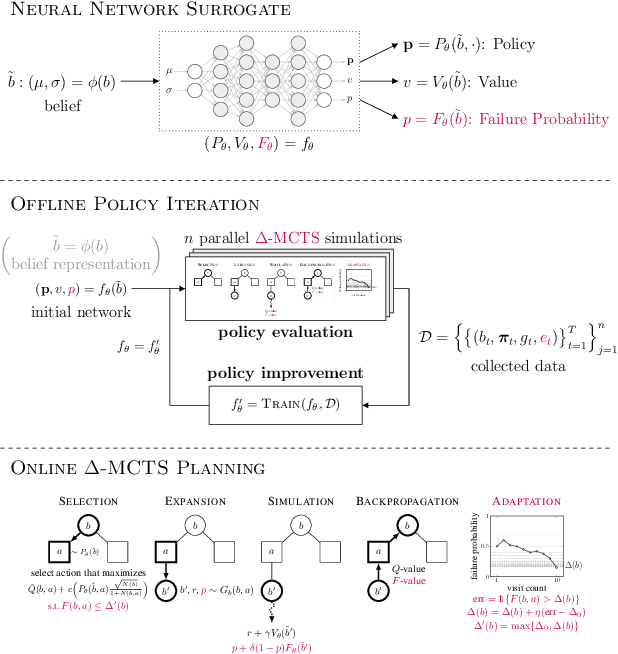
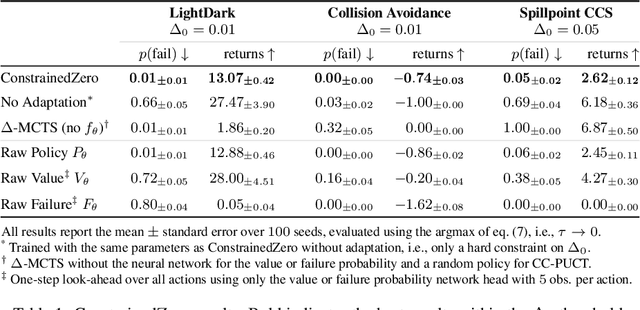
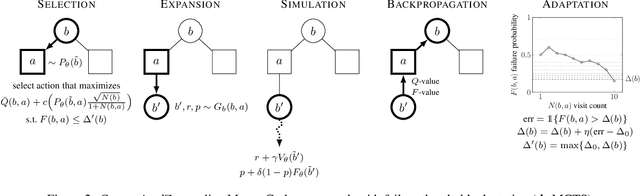
To plan safely in uncertain environments, agents must balance utility with safety constraints. Safe planning problems can be modeled as a chance-constrained partially observable Markov decision process (CC-POMDP) and solutions often use expensive rollouts or heuristics to estimate the optimal value and action-selection policy. This work introduces the ConstrainedZero policy iteration algorithm that solves CC-POMDPs in belief space by learning neural network approximations of the optimal value and policy with an additional network head that estimates the failure probability given a belief. This failure probability guides safe action selection during online Monte Carlo tree search (MCTS). To avoid overemphasizing search based on the failure estimates, we introduce $\Delta$-MCTS, which uses adaptive conformal inference to update the failure threshold during planning. The approach is tested on a safety-critical POMDP benchmark, an aircraft collision avoidance system, and the sustainability problem of safe CO$_2$ storage. Results show that by separating safety constraints from the objective we can achieve a target level of safety without optimizing the balance between rewards and costs.

Formal and Practical Elements for the Certification of Machine Learning Systems

Over the past decade, machine learning has demonstrated impressive results, often surpassing human capabilities in sensing tasks relevant to autonomous flight. Unlike traditional aerospace software, the parameters of machine learning models are not hand-coded nor derived from physics but learned from data. They are automatically adjusted during a training phase, and their values do not usually correspond to physical requirements. As a result, requirements cannot be directly traced to lines of code, hindering the current bottom-up aerospace certification paradigm. This paper attempts to address this gap by 1) demystifying the inner workings and processes to build machine learning models, 2) formally establishing theoretical guarantees given by those processes, and 3) complementing these formal elements with practical considerations to develop a complete certification argument for safety-critical machine learning systems. Based on a scalable statistical verifier, our proposed framework is model-agnostic and tool-independent, making it adaptable to many use cases in the industry. We demonstrate results on a widespread application in autonomous flight: vision-based landing.

BetaZero: Belief-State Planning for Long-Horizon POMDPs using Learned Approximations

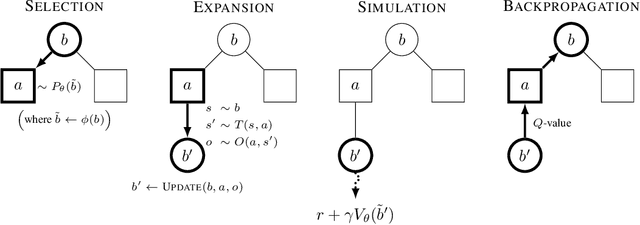
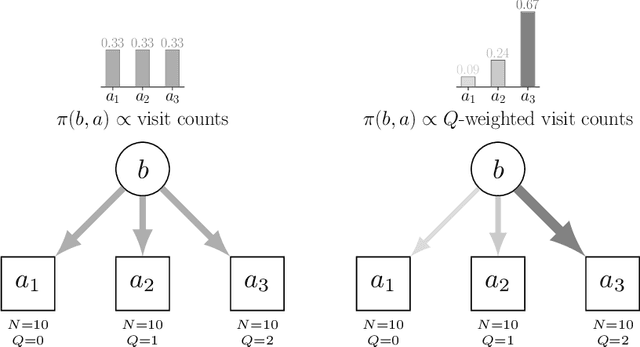
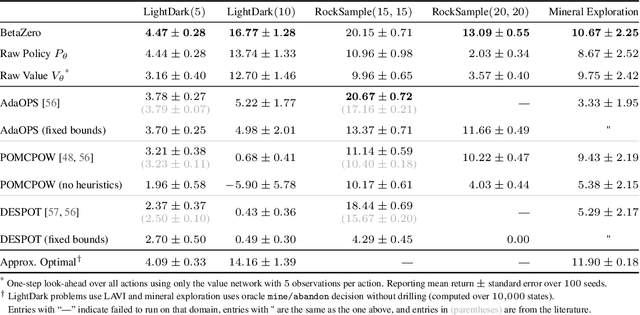
Real-world planning problems$\unicode{x2014}$including autonomous driving and sustainable energy applications like carbon storage and resource exploration$\unicode{x2014}$have recently been modeled as partially observable Markov decision processes (POMDPs) and solved using approximate methods. To solve high-dimensional POMDPs in practice, state-of-the-art methods use online planning with problem-specific heuristics to reduce planning horizons and make the problems tractable. Algorithms that learn approximations to replace heuristics have recently found success in large-scale problems in the fully observable domain. The key insight is the combination of online Monte Carlo tree search with offline neural network approximations of the optimal policy and value function. In this work, we bring this insight to partially observed domains and propose BetaZero, a belief-state planning algorithm for POMDPs. BetaZero learns offline approximations based on accurate belief models to enable online decision making in long-horizon problems. We address several challenges inherent in large-scale partially observable domains; namely challenges of transitioning in stochastic environments, prioritizing action branching with limited search budget, and representing beliefs as input to the network. We apply BetaZero to various well-established benchmark POMDPs found in the literature. As a real-world case study, we test BetaZero on the high-dimensional geological problem of critical mineral exploration. Experiments show that BetaZero outperforms state-of-the-art POMDP solvers on a variety of tasks.

Bayesian Safety Validation for Black-Box Systems

Accurately estimating the probability of failure for safety-critical systems is important for certification. Estimation is often challenging due to high-dimensional input spaces, dangerous test scenarios, and computationally expensive simulators; thus, efficient estimation techniques are important to study. This work reframes the problem of black-box safety validation as a Bayesian optimization problem and introduces an algorithm, Bayesian safety validation, that iteratively fits a probabilistic surrogate model to efficiently predict failures. The algorithm is designed to search for failures, compute the most-likely failure, and estimate the failure probability over an operating domain using importance sampling. We introduce a set of three acquisition functions that focus on reducing uncertainty by covering the design space, optimizing the analytically derived failure boundaries, and sampling the predicted failure regions. Mainly concerned with systems that only output a binary indication of failure, we show that our method also works well in cases where more output information is available. Results show that Bayesian safety validation achieves a better estimate of the probability of failure using orders of magnitude fewer samples and performs well across various safety validation metrics. We demonstrate the algorithm on three test problems with access to ground truth and on a real-world safety-critical subsystem common in autonomous flight: a neural network-based runway detection system. This work is open sourced and currently being used to supplement the FAA certification process of the machine learning components for an autonomous cargo aircraft.

Adaptive Stress Testing of Trajectory Predictions in Flight Management Systems

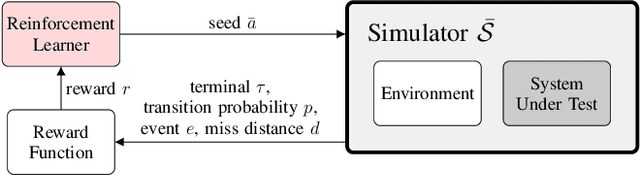
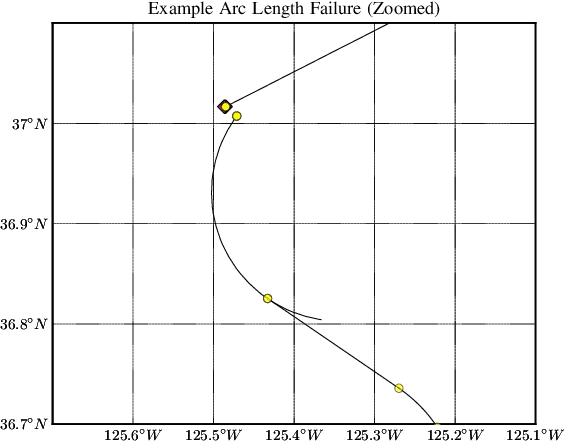
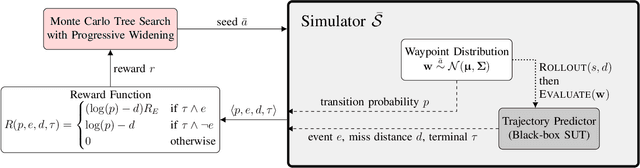
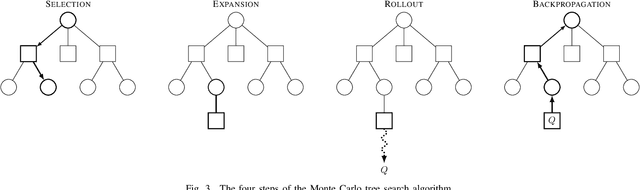
To find failure events and their likelihoods in flight-critical systems, we investigate the use of an advanced black-box stress testing approach called adaptive stress testing. We analyze a trajectory predictor from a developmental commercial flight management system which takes as input a collection of lateral waypoints and en-route environmental conditions. Our aim is to search for failure events relating to inconsistencies in the predicted lateral trajectories. The intention of this work is to find likely failures and report them back to the developers so they can address and potentially resolve shortcomings of the system before deployment. To improve search performance, this work extends the adaptive stress testing formulation to be applied more generally to sequential decision-making problems with episodic reward by collecting the state transitions during the search and evaluating at the end of the simulated rollout. We use a modified Monte Carlo tree search algorithm with progressive widening as our adversarial reinforcement learner. The performance is compared to direct Monte Carlo simulations and to the cross-entropy method as an alternative importance sampling baseline. The goal is to find potential problems otherwise not found by traditional requirements-based testing. Results indicate that our adaptive stress testing approach finds more failures and finds failures with higher likelihood relative to the baseline approaches.

Cross-Entropy Method Variants for Optimization

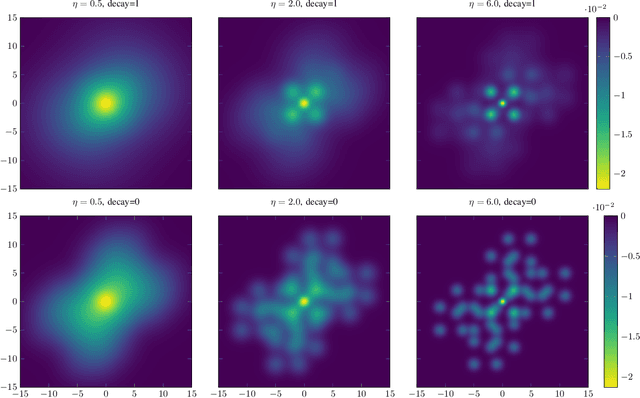
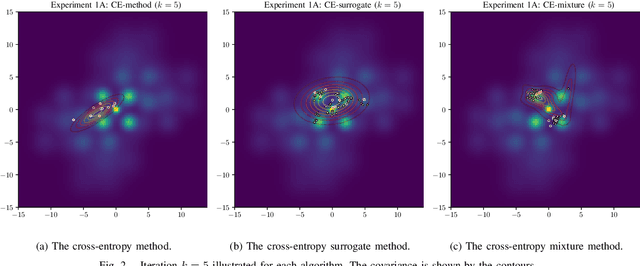
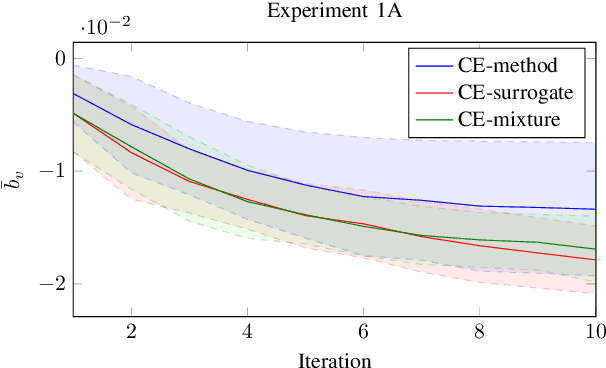
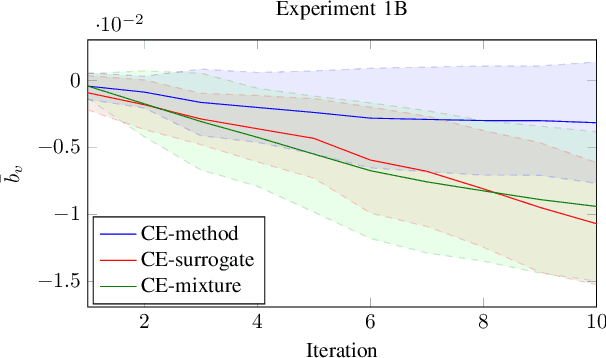
The cross-entropy (CE) method is a popular stochastic method for optimization due to its simplicity and effectiveness. Designed for rare-event simulations where the probability of a target event occurring is relatively small, the CE-method relies on enough objective function calls to accurately estimate the optimal parameters of the underlying distribution. Certain objective functions may be computationally expensive to evaluate, and the CE-method could potentially get stuck in local minima. This is compounded with the need to have an initial covariance wide enough to cover the design space of interest. We introduce novel variants of the CE-method to address these concerns. To mitigate expensive function calls, during optimization we use every sample to build a surrogate model to approximate the objective function. The surrogate model augments the belief of the objective function with less expensive evaluations. We use a Gaussian process for our surrogate model to incorporate uncertainty in the predictions which is especially helpful when dealing with sparse data. To address local minima convergence, we use Gaussian mixture models to encourage exploration of the design space. We experiment with evaluation scheduling techniques to reallocate true objective function calls earlier in the optimization when the covariance is the largest. To test our approach, we created a parameterized test objective function with many local minima and a single global minimum. Our test function can be adjusted to control the spread and distinction of the minima. Experiments were run to stress the cross-entropy method variants and results indicate that the surrogate model-based approach reduces local minima convergence using the same number of function evaluations.

A Survey of Algorithms for Black-Box Safety Validation

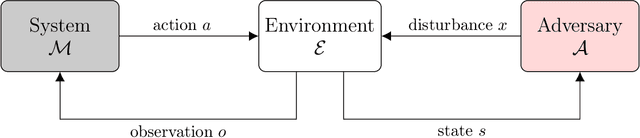
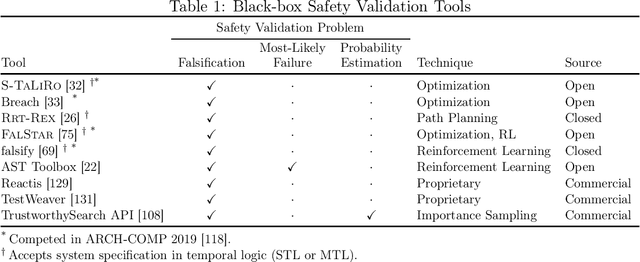
Autonomous and semi-autonomous systems for safety-critical applications require rigorous testing before deployment. Due to the complexity of these systems, formal verification may be impossible and real-world testing may be dangerous during development. Therefore, simulation-based techniques have been developed that treat the system under test as a black box during testing. Safety validation tasks include finding disturbances to the system that cause it to fail (falsification), finding the most-likely failure, and estimating the probability that the system fails. Motivated by the prevalence of safety-critical artificial intelligence, this work provides a survey of state-of-the-art safety validation techniques with a focus on applied algorithms and their modifications for the safety validation problem. We present and discuss algorithms in the domains of optimization, path planning, reinforcement learning, and importance sampling. Problem decomposition techniques are presented to help scale algorithms to large state spaces, and a brief overview of safety-critical applications is given, including autonomous vehicles and aircraft collision avoidance systems. Finally, we present a survey of existing academic and commercially available safety validation tools.