Cross-Entropy Method Variants for Optimization
Paper and Code
Sep 18, 2020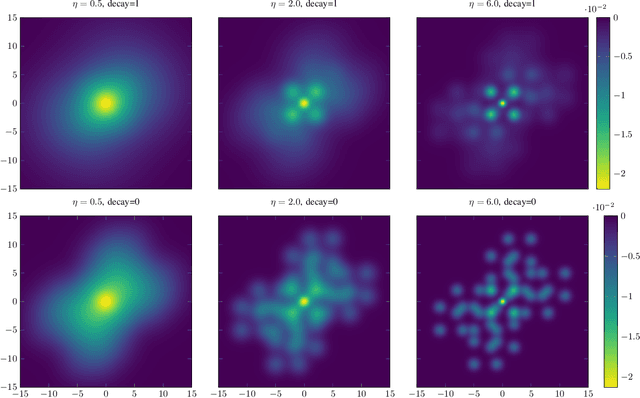
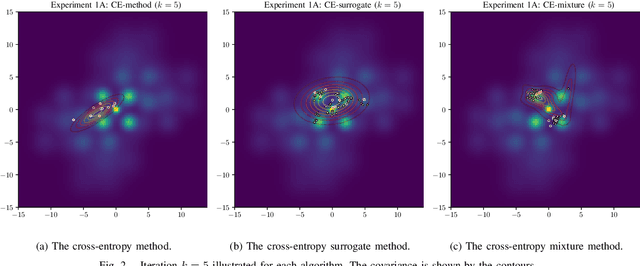
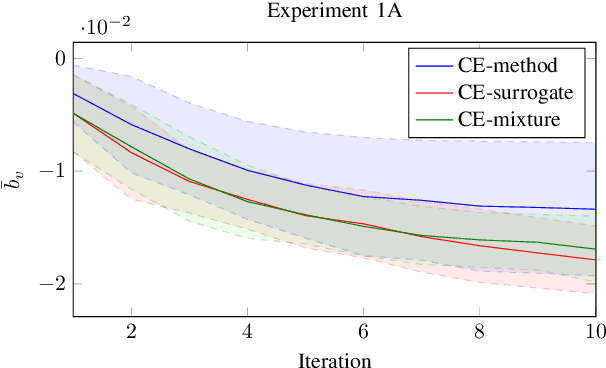
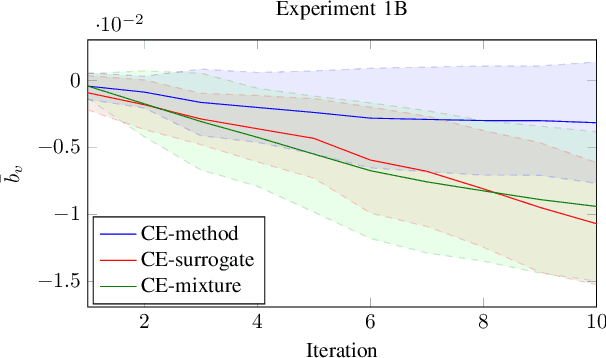
The cross-entropy (CE) method is a popular stochastic method for optimization due to its simplicity and effectiveness. Designed for rare-event simulations where the probability of a target event occurring is relatively small, the CE-method relies on enough objective function calls to accurately estimate the optimal parameters of the underlying distribution. Certain objective functions may be computationally expensive to evaluate, and the CE-method could potentially get stuck in local minima. This is compounded with the need to have an initial covariance wide enough to cover the design space of interest. We introduce novel variants of the CE-method to address these concerns. To mitigate expensive function calls, during optimization we use every sample to build a surrogate model to approximate the objective function. The surrogate model augments the belief of the objective function with less expensive evaluations. We use a Gaussian process for our surrogate model to incorporate uncertainty in the predictions which is especially helpful when dealing with sparse data. To address local minima convergence, we use Gaussian mixture models to encourage exploration of the design space. We experiment with evaluation scheduling techniques to reallocate true objective function calls earlier in the optimization when the covariance is the largest. To test our approach, we created a parameterized test objective function with many local minima and a single global minimum. Our test function can be adjusted to control the spread and distinction of the minima. Experiments were run to stress the cross-entropy method variants and results indicate that the surrogate model-based approach reduces local minima convergence using the same number of function evaluations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge