Intelligent prospector v2.0: exploration drill planning under epistemic model uncertainty

Optimal Bayesian decision making on what geoscientific data to acquire requires stating a prior model of uncertainty. Data acquisition is then optimized by reducing uncertainty on some property of interest maximally, and on average. In the context of exploration, very few, sometimes no data at all, is available prior to data acquisition planning. The prior model therefore needs to include human interpretations on the nature of spatial variability, or on analogue data deemed relevant for the area being explored. In mineral exploration, for example, humans may rely on conceptual models on the genesis of the mineralization to define multiple hypotheses, each representing a specific spatial variability of mineralization. More often than not, after the data is acquired, all of the stated hypotheses may be proven incorrect, i.e. falsified, hence prior hypotheses need to be revised, or additional hypotheses generated. Planning data acquisition under wrong geological priors is likely to be inefficient since the estimated uncertainty on the target property is incorrect, hence uncertainty may not be reduced at all. In this paper, we develop an intelligent agent based on partially observable Markov decision processes that plans optimally in the case of multiple geological or geoscientific hypotheses on the nature of spatial variability. Additionally, the artificial intelligence is equipped with a method that allows detecting, early on, whether the human stated hypotheses are incorrect, thereby saving considerable expense in data acquisition. Our approach is tested on a sediment-hosted copper deposit, and the algorithm presented has aided in the characterization of an ultra high-grade deposit in Zambia in 2023.

BetaZero: Belief-State Planning for Long-Horizon POMDPs using Learned Approximations

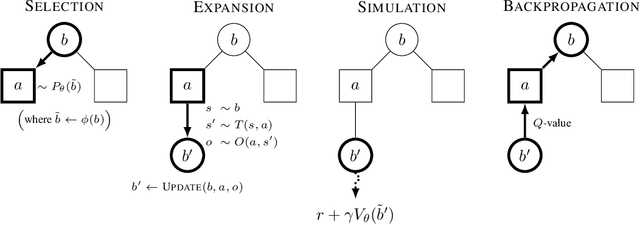
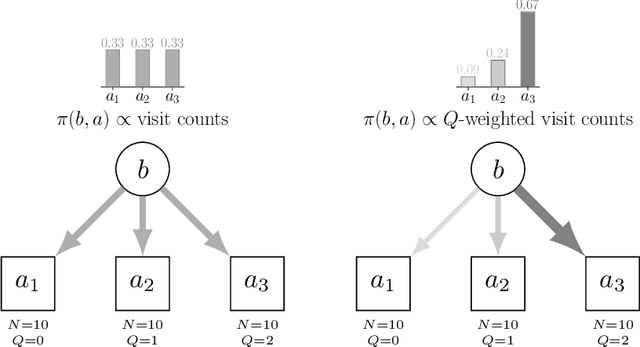
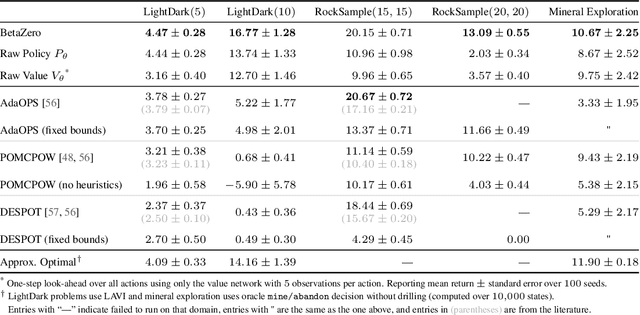
Real-world planning problems$\unicode{x2014}$including autonomous driving and sustainable energy applications like carbon storage and resource exploration$\unicode{x2014}$have recently been modeled as partially observable Markov decision processes (POMDPs) and solved using approximate methods. To solve high-dimensional POMDPs in practice, state-of-the-art methods use online planning with problem-specific heuristics to reduce planning horizons and make the problems tractable. Algorithms that learn approximations to replace heuristics have recently found success in large-scale problems in the fully observable domain. The key insight is the combination of online Monte Carlo tree search with offline neural network approximations of the optimal policy and value function. In this work, we bring this insight to partially observed domains and propose BetaZero, a belief-state planning algorithm for POMDPs. BetaZero learns offline approximations based on accurate belief models to enable online decision making in long-horizon problems. We address several challenges inherent in large-scale partially observable domains; namely challenges of transitioning in stochastic environments, prioritizing action branching with limited search budget, and representing beliefs as input to the network. We apply BetaZero to various well-established benchmark POMDPs found in the literature. As a real-world case study, we test BetaZero on the high-dimensional geological problem of critical mineral exploration. Experiments show that BetaZero outperforms state-of-the-art POMDP solvers on a variety of tasks.