Anomaly detection in dynamic networks

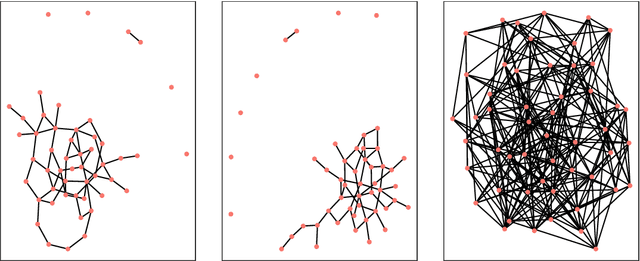
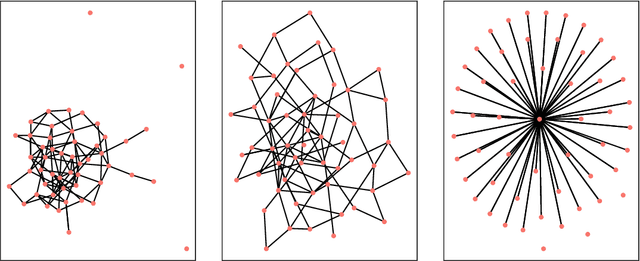
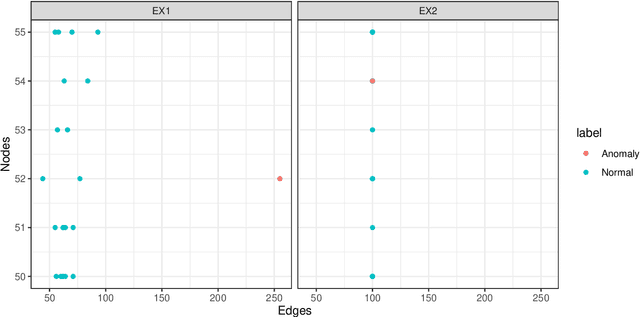
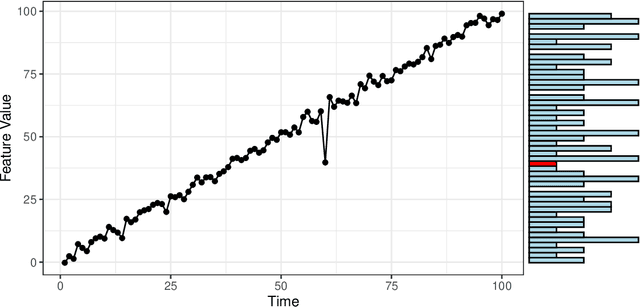
Detecting anomalies from a series of temporal networks has many applications, including road accidents in transport networks and suspicious events in social networks. While there are many methods for network anomaly detection, statistical methods are under utilised in this space even though they have a long history and proven capability in handling temporal dependencies. In this paper, we introduce \textit{oddnet}, a feature-based network anomaly detection method that uses time series methods to model temporal dependencies. We demonstrate the effectiveness of oddnet on synthetic and real-world datasets. The R package oddnet implements this algorithm.

Forecast combinations: an over 50-year review

Forecast combinations have flourished remarkably in the forecasting community and, in recent years, have become part of the mainstream of forecasting research and activities. Combining multiple forecasts produced from the single (target) series is now widely used to improve accuracy through the integration of information gleaned from different sources, thereby mitigating the risk of identifying a single "best" forecast. Combination schemes have evolved from simple combination methods without estimation, to sophisticated methods involving time-varying weights, nonlinear combinations, correlations among components, and cross-learning. They include combining point forecasts, and combining probabilistic forecasts. This paper provides an up-to-date review of the extensive literature on forecast combinations, together with reference to available open-source software implementations. We discuss the potential and limitations of various methods and highlight how these ideas have developed over time. Some important issues concerning the utility of forecast combinations are also surveyed. Finally, we conclude with current research gaps and potential insights for future research.

LoMEF: A Framework to Produce Local Explanations for Global Model Time Series Forecasts

Global Forecasting Models (GFM) that are trained across a set of multiple time series have shown superior results in many forecasting competitions and real-world applications compared with univariate forecasting approaches. One aspect of the popularity of statistical forecasting models such as ETS and ARIMA is their relative simplicity and interpretability (in terms of relevant lags, trend, seasonality, and others), while GFMs typically lack interpretability, especially towards particular time series. This reduces the trust and confidence of the stakeholders when making decisions based on the forecasts without being able to understand the predictions. To mitigate this problem, in this work, we propose a novel local model-agnostic interpretability approach to explain the forecasts from GFMs. We train simpler univariate surrogate models that are considered interpretable (e.g., ETS) on the predictions of the GFM on samples within a neighbourhood that we obtain through bootstrapping or straightforwardly as the one-step-ahead global black-box model forecasts of the time series which needs to be explained. After, we evaluate the explanations for the forecasts of the global models in both qualitative and quantitative aspects such as accuracy, fidelity, stability and comprehensibility, and are able to show the benefits of our approach.

A Look at the Evaluation Setup of the M5 Forecasting Competition

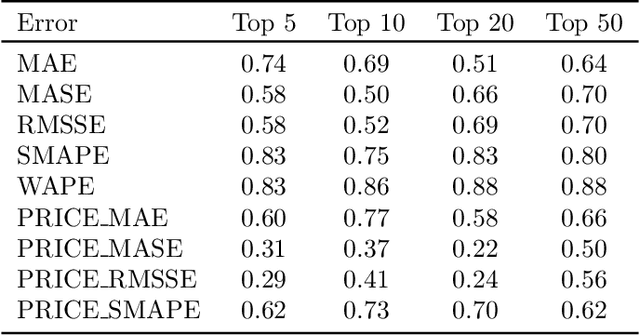
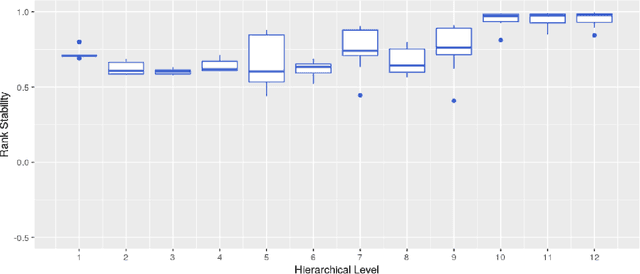
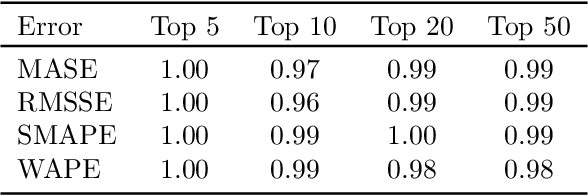
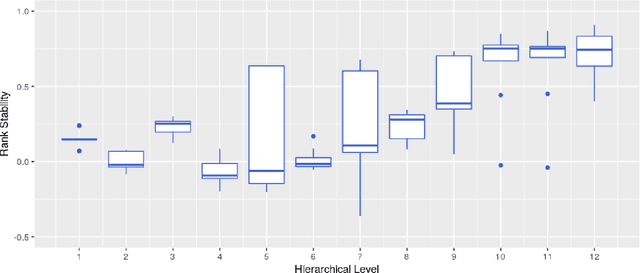
Forecast evaluation plays a key role in how empirical evidence shapes the development of the discipline. Domain experts are interested in error measures relevant for their decision making needs. Such measures may produce unreliable results. Although reliability properties of several metrics have already been discussed, it has hardly been quantified in an objective way. We propose a measure named Rank Stability, which evaluates how much the rankings of an experiment differ in between similar datasets, when the models and errors are constant. We use this to study the evaluation setup of the M5. We find that the evaluation setup of the M5 is less reliable than other measures. The main drivers of instability are hierarchical aggregation and scaling. Price-weighting reduces the stability of all tested error measures. Scale normalization of the M5 error measure results in less stability than other scale-free errors. Hierarchical levels taken separately are less stable with more aggregation, and their combination is even less stable than individual levels. We also show positive tradeoffs of retaining aggregation importance without affecting stability. Aggregation and stability can be linked to the influence of much debated magic numbers. Many of our findings can be applied to general hierarchical forecast benchmarking.

Modern strategies for time series regression

This paper discusses several modern approaches to regression analysis involving time series data where some of the predictor variables are also indexed by time. We discuss classical statistical approaches as well as methods that have been proposed recently in the machine learning literature. The approaches are compared and contrasted, and it will be seen that there are advantages and disadvantages to most currently available approaches. There is ample room for methodological developments in this area. The work is motivated by an application involving the prediction of water levels as a function of rainfall and other climate variables in an aquifer in eastern Australia.

Model selection in reconciling hierarchical time series

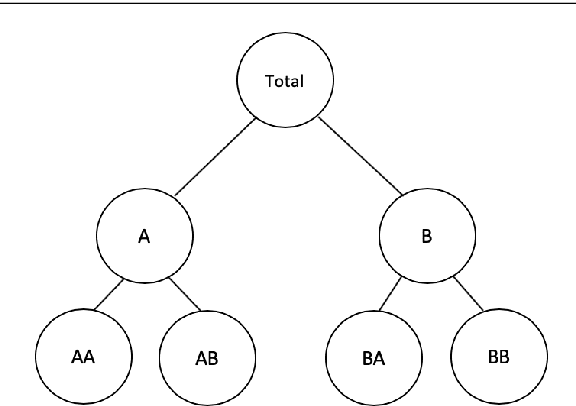
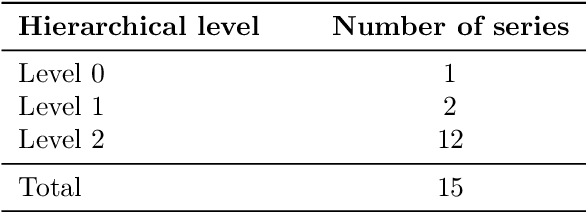
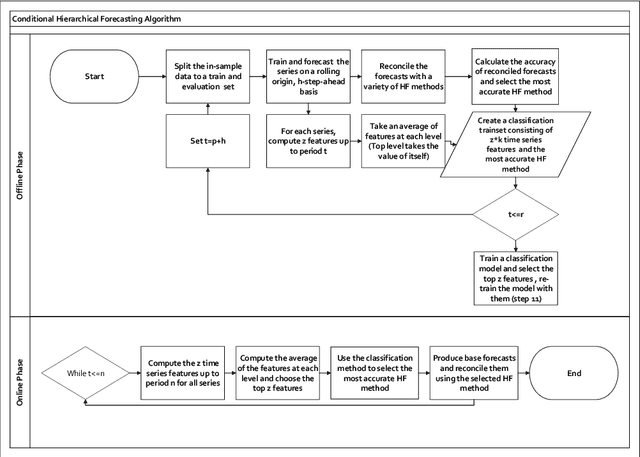
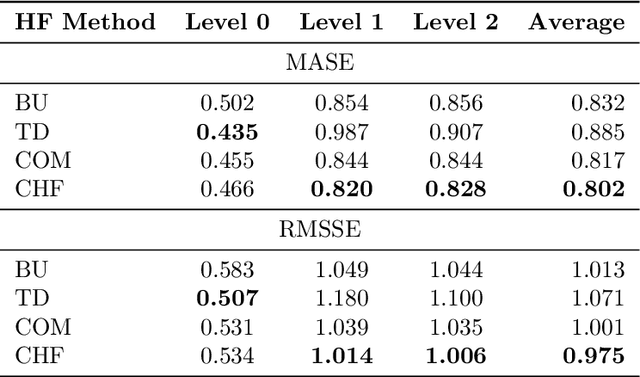
Model selection has been proven an effective strategy for improving accuracy in time series forecasting applications. However, when dealing with hierarchical time series, apart from selecting the most appropriate forecasting model, forecasters have also to select a suitable method for reconciling the base forecasts produced for each series to make sure they are coherent. Although some hierarchical forecasting methods like minimum trace are strongly supported both theoretically and empirically for reconciling the base forecasts, there are still circumstances under which they might not produce the most accurate results, being outperformed by other methods. In this paper we propose an approach for dynamically selecting the most appropriate hierarchical forecasting method and succeeding better forecasting accuracy along with coherence. The approach, to be called conditional hierarchical forecasting, is based on Machine Learning classification methods and uses time series features as leading indicators for performing the selection for each hierarchy examined considering a variety of alternatives. Our results suggest that conditional hierarchical forecasting leads to significantly more accurate forecasts than standard approaches, especially at lower hierarchical levels.

Principles and Algorithms for Forecasting Groups of Time Series: Locality and Globality

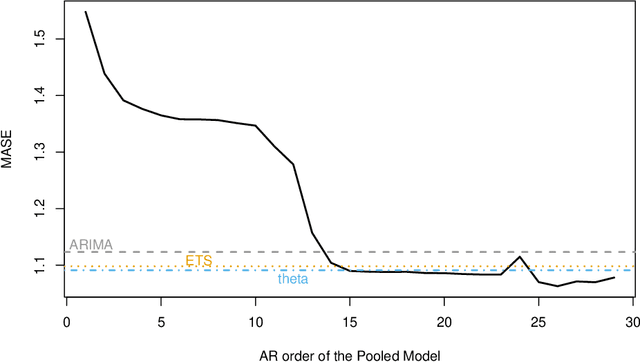
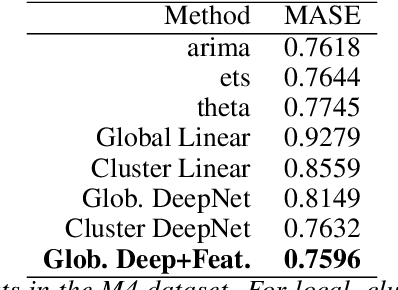
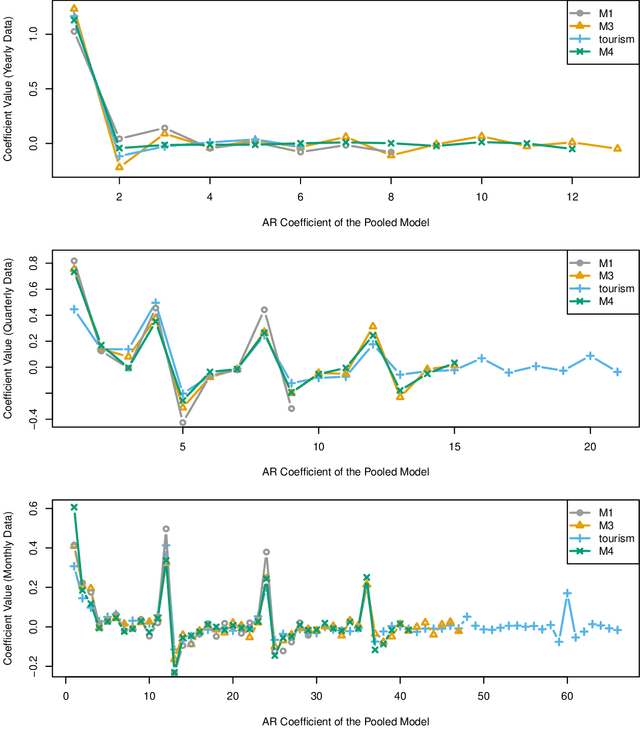
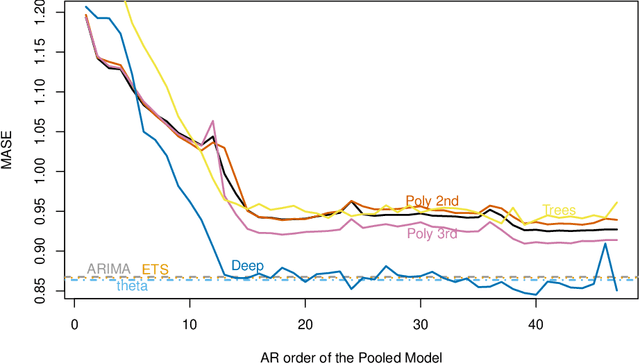
Forecasting groups of time series is of increasing practical importance, e.g. forecasting the demand for multiple products offered by a retailer or server loads within a data center. The local approach to this problem considers each time series separately and fits a function or model to each series. The global approach fits a single function to all series. For groups of similar time series, global methods outperform the more established local methods. However, recent results show good performance of global models even in heterogeneous datasets. This suggests a more general applicability of global methods, potentially leading to more accurate tools and new scenarios to study. Formalizing the setting of forecasting a set of time series with local and global methods, we provide the following contributions: 1) Global methods are not more restrictive than local methods, both can produce the same forecasts without any assumptions about similarity of the series. Global models can succeed in a wider range of problems than previously thought. 2) Basic generalization bounds for local and global algorithms. The complexity of local methods grows with the size of the set while it remains constant for global methods. In large datasets, a global algorithm can afford to be quite complex and still benefit from better generalization. These bounds serve to clarify and support recent experimental results in the field, and guide the design of new algorithms. For the class of autoregressive models, this implies that global models can have much larger memory than local methods. 3) In an extensive empirical study, purposely naive algorithms derived from these principles, such as global linear models or deep networks result in superior accuracy. In particular, global linear models can provide competitive accuracy with two orders of magnitude fewer parameters than local methods.

Hierarchical forecast reconciliation with machine learning

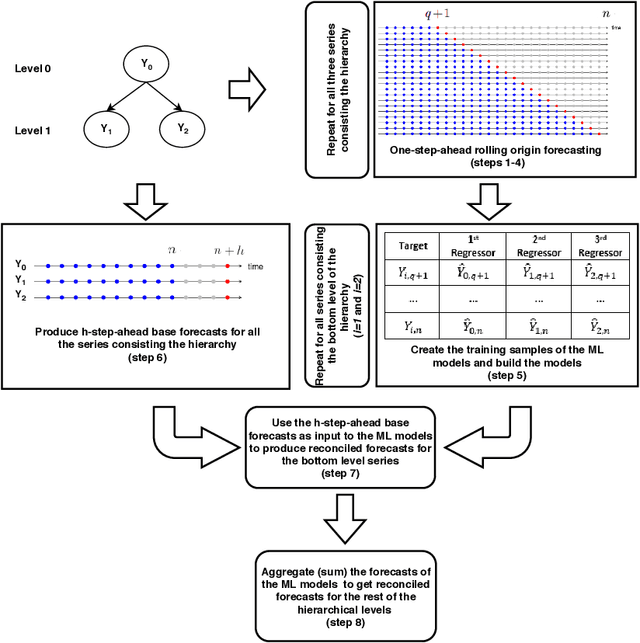
Hierarchical forecasting methods have been widely used to support aligned decision-making by providing coherent forecasts at different aggregation levels. Traditional hierarchical forecasting approaches, such as the bottom-up and top-down methods, focus on a particular aggregation level to anchor the forecasts. During the past decades, these have been replaced by a variety of linear combination approaches that exploit information from the complete hierarchy to produce more accurate forecasts. However, the performance of these combination methods depends on the particularities of the examined series and their relationships. This paper proposes a novel hierarchical forecasting approach based on machine learning that deals with these limitations in three important ways. First, the proposed method allows for a non-linear combination of the base forecasts, thus being more general than the linear approaches. Second, it structurally combines the objectives of improved post-sample empirical forecasting accuracy and coherence. Finally, due to its non-linear nature, our approach selectively combines the base forecasts in a direct and automated way without requiring that the complete information must be used for producing reconciled forecasts for each series and level. The proposed method is evaluated both in terms of accuracy and bias using two different data sets coming from the tourism and retail industries. Our results suggest that the proposed method gives superior point forecasts than existing approaches, especially when the series comprising the hierarchy are not characterized by the same patterns.

Machine learning applications in time series hierarchical forecasting

Hierarchical forecasting (HF) is needed in many situations in the supply chain (SC) because managers often need different levels of forecasts at different levels of SC to make a decision. Top-Down (TD), Bottom-Up (BU) and Optimal Combination (COM) are common HF models. These approaches are static and often ignore the dynamics of the series while disaggregating them. Consequently, they may fail to perform well if the investigated group of time series are subject to large changes such as during the periods of promotional sales. We address the HF problem of predicting real-world sales time series that are highly impacted by promotion. We use three machine learning (ML) models to capture sales variations over time. Artificial neural networks (ANN), extreme gradient boosting (XGboost), and support vector regression (SVR) algorithms are used to estimate the proportions of lower-level time series from the upper level. We perform an in-depth analysis of 61 groups of time series with different volatilities and show that ML models are competitive and outperform some well-established models in the literature.

GRATIS: GeneRAting TIme Series with diverse and controllable characteristics

The explosion of time series data in recent years has brought a flourish of new time series analysis methods, for forecasting, clustering, classification and other tasks. The evaluation of these new methods requires a diverse collection of time series benchmarking data to enable reliable comparisons against alternative approaches. We propose GeneRAting TIme Series with diverse and controllable characteristics, named GRATIS, with the use of mixture autoregressive (MAR) models. We generate sets of time series using MAR models and investigate the diversity and coverage of the generated time series in a time series feature space. By tuning the parameters of the MAR models, GRATIS is also able to efficiently generate new time series with controllable features. In general, as a costless surrogate to the traditional data collection approach, GRATIS can be used as an evaluation tool for tasks such as time series forecasting and classification. We illustrate the usefulness of our time series generation process through a time series forecasting application.