Comparison and Evaluation of Methods for a Predict+Optimize Problem in Renewable Energy

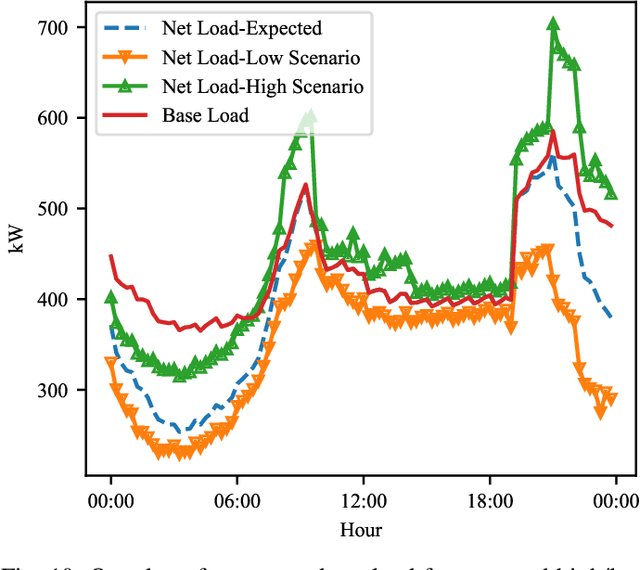
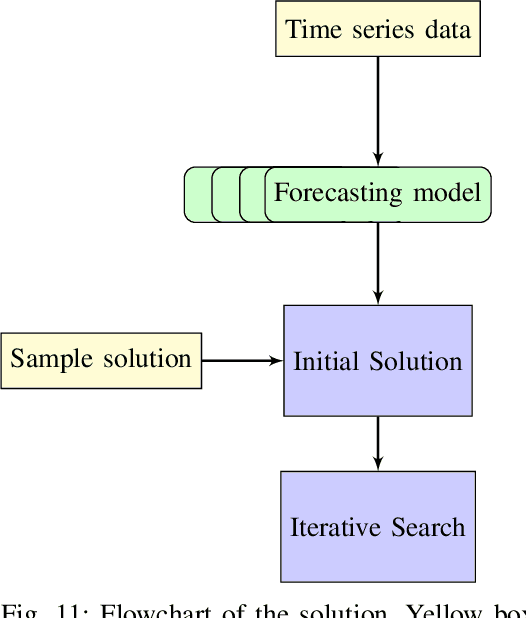
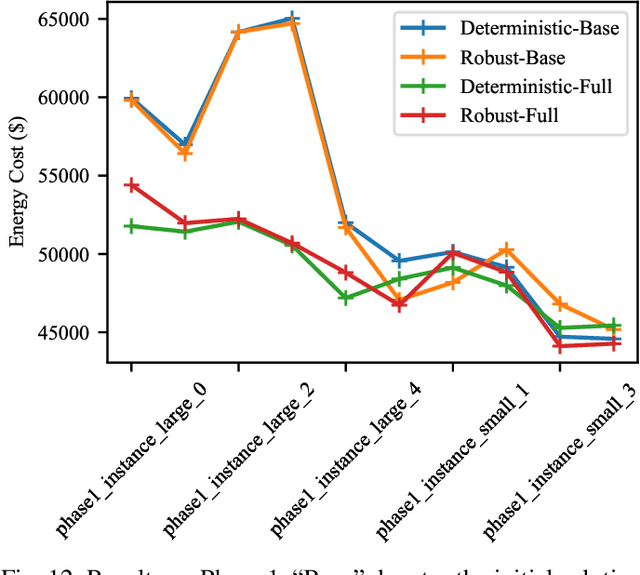
Algorithms that involve both forecasting and optimization are at the core of solutions to many difficult real-world problems, such as in supply chains (inventory optimization), traffic, and in the transition towards carbon-free energy generation in battery/load/production scheduling in sustainable energy systems. Typically, in these scenarios we want to solve an optimization problem that depends on unknown future values, which therefore need to be forecast. As both forecasting and optimization are difficult problems in their own right, relatively few research has been done in this area. This paper presents the findings of the ``IEEE-CIS Technical Challenge on Predict+Optimize for Renewable Energy Scheduling," held in 2021. We present a comparison and evaluation of the seven highest-ranked solutions in the competition, to provide researchers with a benchmark problem and to establish the state of the art for this benchmark, with the aim to foster and facilitate research in this area. The competition used data from the Monash Microgrid, as well as weather data and energy market data. It then focused on two main challenges: forecasting renewable energy production and demand, and obtaining an optimal schedule for the activities (lectures) and on-site batteries that lead to the lowest cost of energy. The most accurate forecasts were obtained by gradient-boosted tree and random forest models, and optimization was mostly performed using mixed integer linear and quadratic programming. The winning method predicted different scenarios and optimized over all scenarios jointly using a sample average approximation method.

FRANS: Automatic Feature Extraction for Time Series Forecasting

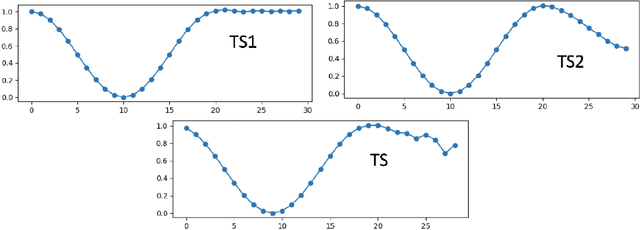
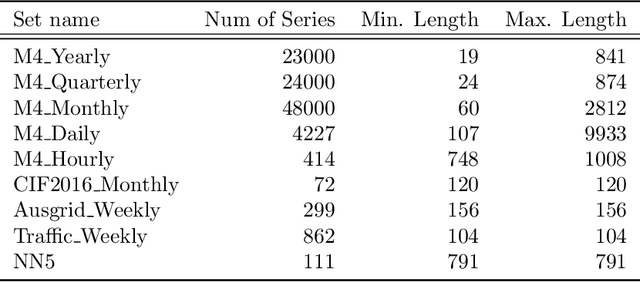
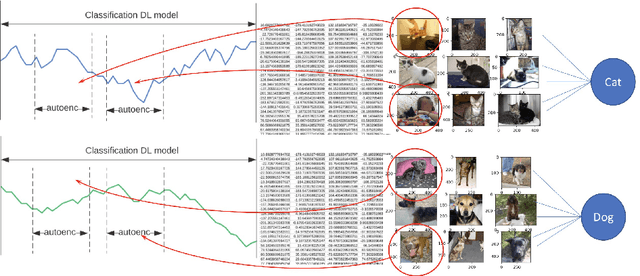
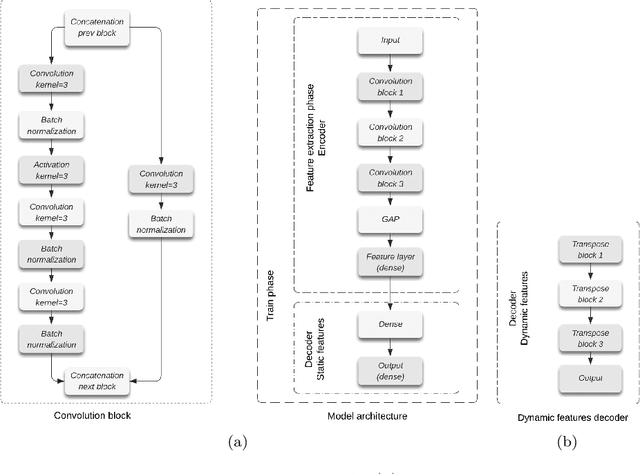
Feature extraction methods help in dimensionality reduction and capture relevant information. In time series forecasting (TSF), features can be used as auxiliary information to achieve better accuracy. Traditionally, features used in TSF are handcrafted, which requires domain knowledge and significant data-engineering work. In this research, we first introduce a notion of static and dynamic features, which then enables us to develop our autonomous Feature Retrieving Autoregressive Network for Static features (FRANS) that does not require domain knowledge. The method is based on a CNN classifier that is trained to create for each series a collective and unique class representation either from parts of the series or, if class labels are available, from a set of series of the same class. It allows to discriminate series with similar behaviour but from different classes and makes the features extracted from the classifier to be maximally discriminatory. We explore the interpretability of our features, and evaluate the prediction capabilities of the method within the forecasting meta-learning environment FFORMA. Our results show that our features lead to improvement in accuracy in most situations. Once trained our approach creates features orders of magnitude faster than statistical methods.

A Look at the Evaluation Setup of the M5 Forecasting Competition

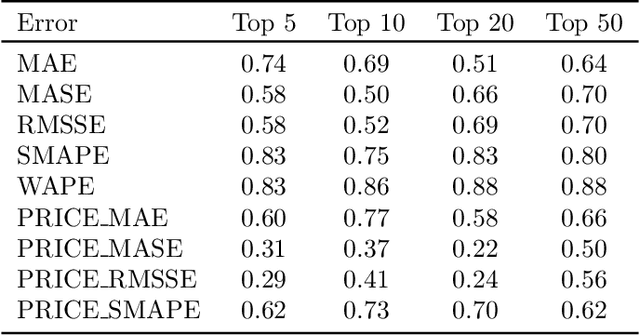
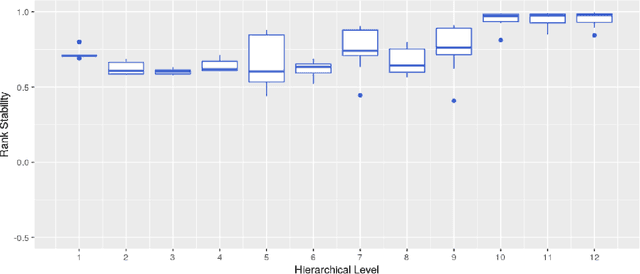
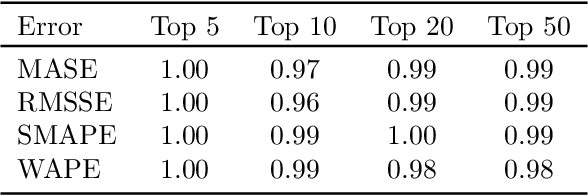
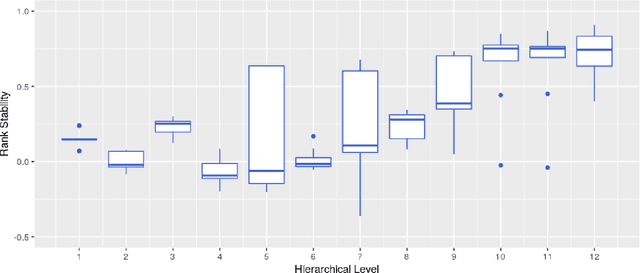
Forecast evaluation plays a key role in how empirical evidence shapes the development of the discipline. Domain experts are interested in error measures relevant for their decision making needs. Such measures may produce unreliable results. Although reliability properties of several metrics have already been discussed, it has hardly been quantified in an objective way. We propose a measure named Rank Stability, which evaluates how much the rankings of an experiment differ in between similar datasets, when the models and errors are constant. We use this to study the evaluation setup of the M5. We find that the evaluation setup of the M5 is less reliable than other measures. The main drivers of instability are hierarchical aggregation and scaling. Price-weighting reduces the stability of all tested error measures. Scale normalization of the M5 error measure results in less stability than other scale-free errors. Hierarchical levels taken separately are less stable with more aggregation, and their combination is even less stable than individual levels. We also show positive tradeoffs of retaining aggregation importance without affecting stability. Aggregation and stability can be linked to the influence of much debated magic numbers. Many of our findings can be applied to general hierarchical forecast benchmarking.

Monash Time Series Forecasting Archive

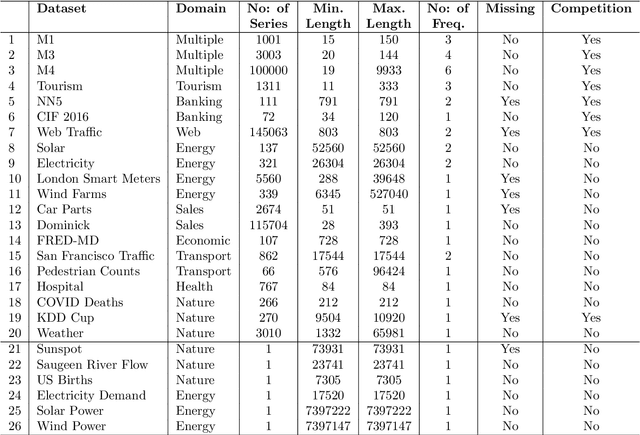
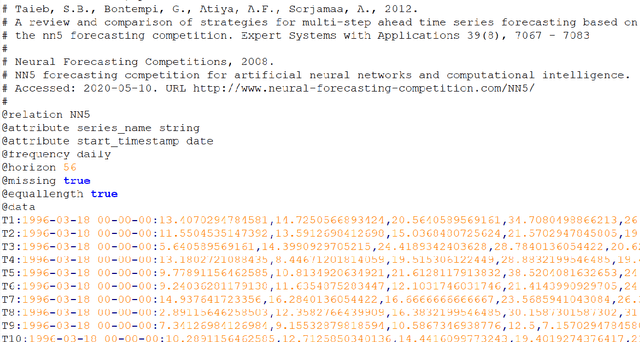
Many businesses and industries nowadays rely on large quantities of time series data making time series forecasting an important research area. Global forecasting models that are trained across sets of time series have shown a huge potential in providing accurate forecasts compared with the traditional univariate forecasting models that work on isolated series. However, there are currently no comprehensive time series archives for forecasting that contain datasets of time series from similar sources available for the research community to evaluate the performance of new global forecasting algorithms over a wide variety of datasets. In this paper, we present such a comprehensive time series forecasting archive containing 20 publicly available time series datasets from varied domains, with different characteristics in terms of frequency, series lengths, and inclusion of missing values. We also characterise the datasets, and identify similarities and differences among them, by conducting a feature analysis. Furthermore, we present the performance of a set of standard baseline forecasting methods over all datasets across eight error metrics, for the benefit of researchers using the archive to benchmark their forecasting algorithms.

A Strong Baseline for Weekly Time Series Forecasting

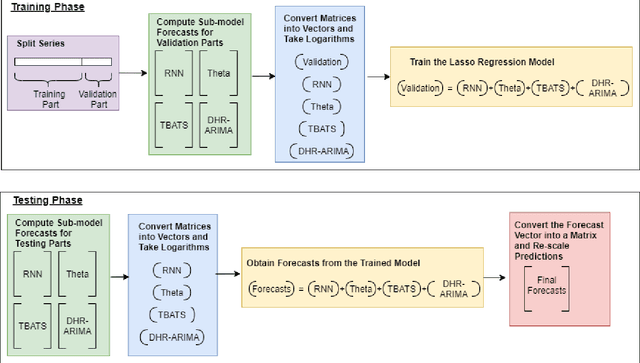
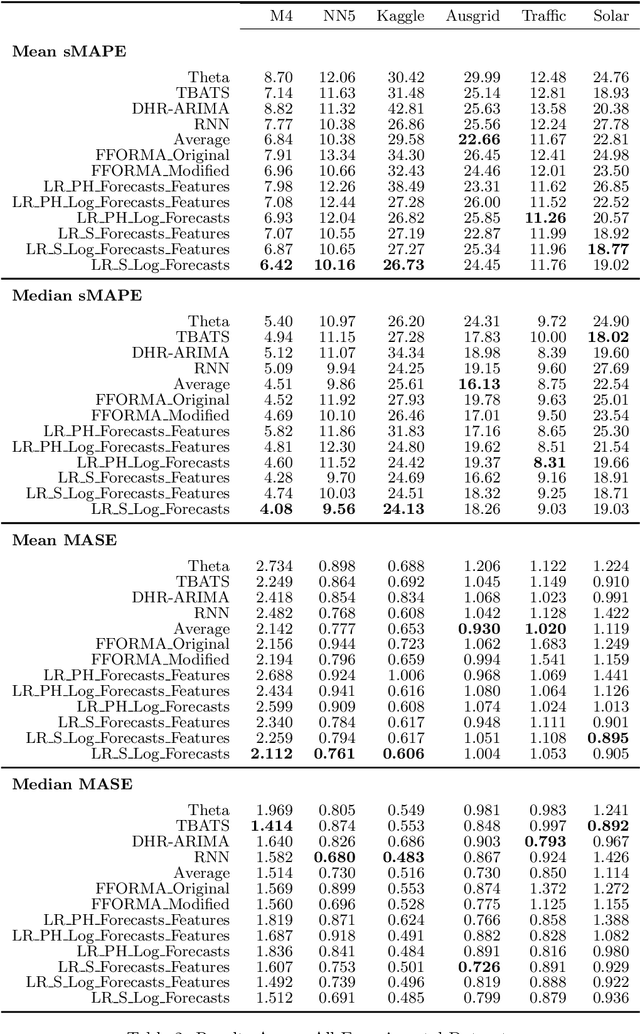
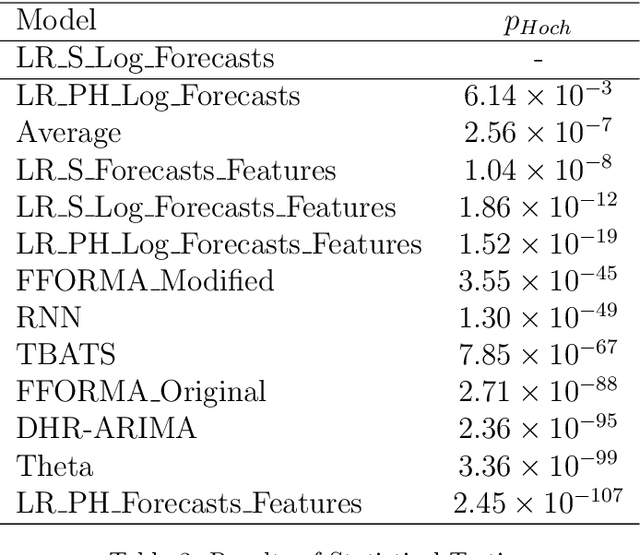
Many businesses and industries require accurate forecasts for weekly time series nowadays. The forecasting literature however does not currently provide easy-to-use, automatic, reproducible and accurate approaches dedicated to this task. We propose a forecasting method that can be used as a strong baseline in this domain, leveraging state-of-the-art forecasting techniques, forecast combination, and global modelling. Our approach uses four base forecasting models specifically suitable for forecasting weekly data: a global Recurrent Neural Network model, Theta, Trigonometric Box-Cox ARMA Trend Seasonal (TBATS), and Dynamic Harmonic Regression ARIMA (DHR-ARIMA). Those are then optimally combined using a lasso regression stacking approach. We evaluate the performance of our method against a set of state-of-the-art weekly forecasting models on six datasets. Across four evaluation metrics, we show that our method consistently outperforms the benchmark methods by a considerable margin with statistical significance. In particular, our model can produce the most accurate forecasts, in terms of mean sMAPE, for the M4 weekly dataset.

Principles and Algorithms for Forecasting Groups of Time Series: Locality and Globality

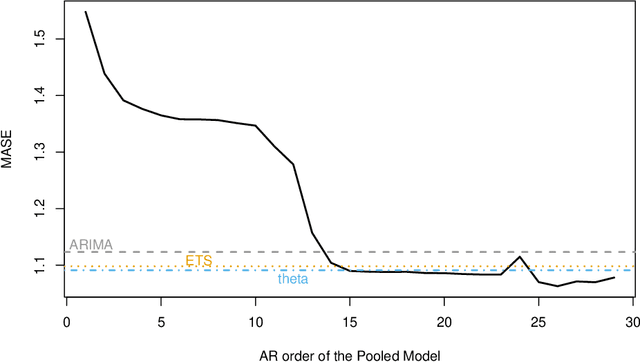
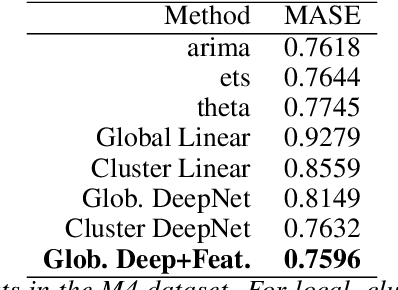
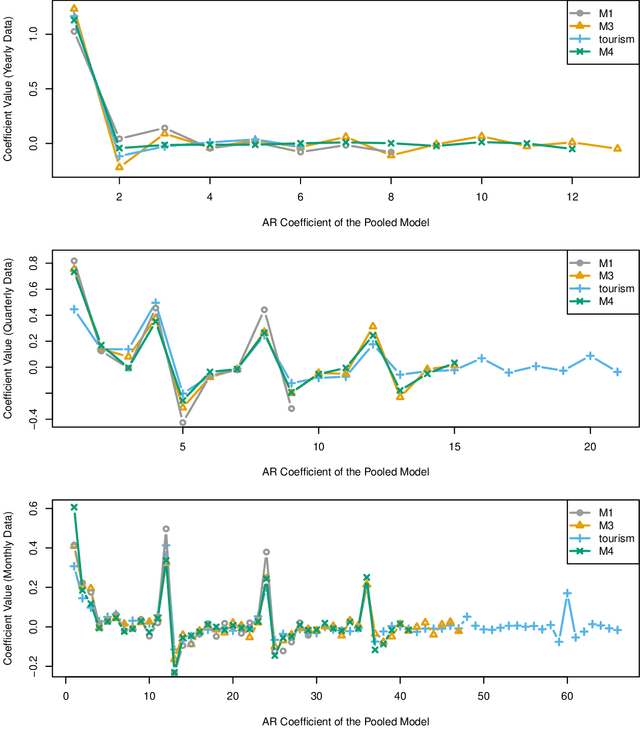
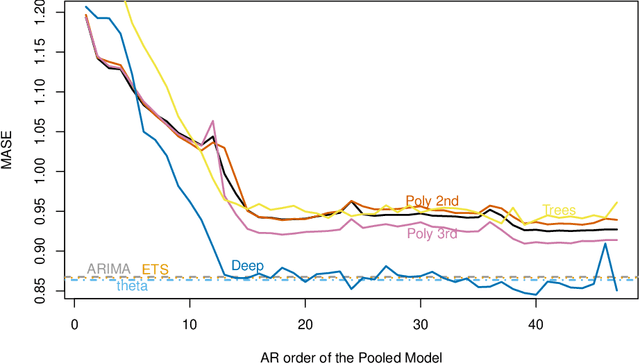
Forecasting groups of time series is of increasing practical importance, e.g. forecasting the demand for multiple products offered by a retailer or server loads within a data center. The local approach to this problem considers each time series separately and fits a function or model to each series. The global approach fits a single function to all series. For groups of similar time series, global methods outperform the more established local methods. However, recent results show good performance of global models even in heterogeneous datasets. This suggests a more general applicability of global methods, potentially leading to more accurate tools and new scenarios to study. Formalizing the setting of forecasting a set of time series with local and global methods, we provide the following contributions: 1) Global methods are not more restrictive than local methods, both can produce the same forecasts without any assumptions about similarity of the series. Global models can succeed in a wider range of problems than previously thought. 2) Basic generalization bounds for local and global algorithms. The complexity of local methods grows with the size of the set while it remains constant for global methods. In large datasets, a global algorithm can afford to be quite complex and still benefit from better generalization. These bounds serve to clarify and support recent experimental results in the field, and guide the design of new algorithms. For the class of autoregressive models, this implies that global models can have much larger memory than local methods. 3) In an extensive empirical study, purposely naive algorithms derived from these principles, such as global linear models or deep networks result in superior accuracy. In particular, global linear models can provide competitive accuracy with two orders of magnitude fewer parameters than local methods.