A Look at the Evaluation Setup of the M5 Forecasting Competition
Paper and Code
Aug 08, 2021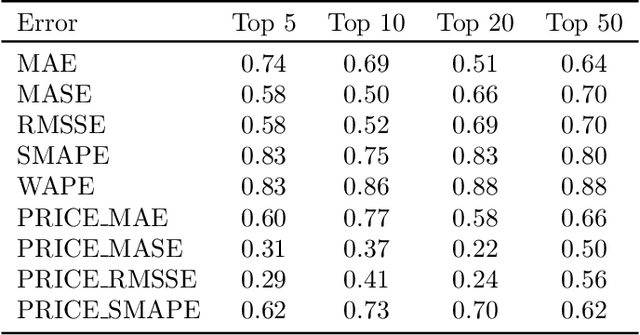
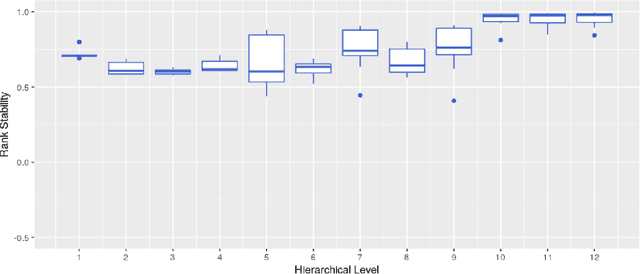
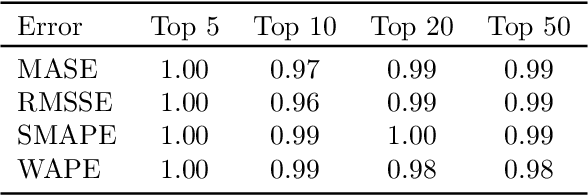
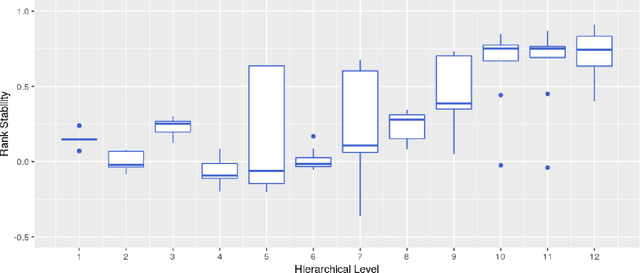
Forecast evaluation plays a key role in how empirical evidence shapes the development of the discipline. Domain experts are interested in error measures relevant for their decision making needs. Such measures may produce unreliable results. Although reliability properties of several metrics have already been discussed, it has hardly been quantified in an objective way. We propose a measure named Rank Stability, which evaluates how much the rankings of an experiment differ in between similar datasets, when the models and errors are constant. We use this to study the evaluation setup of the M5. We find that the evaluation setup of the M5 is less reliable than other measures. The main drivers of instability are hierarchical aggregation and scaling. Price-weighting reduces the stability of all tested error measures. Scale normalization of the M5 error measure results in less stability than other scale-free errors. Hierarchical levels taken separately are less stable with more aggregation, and their combination is even less stable than individual levels. We also show positive tradeoffs of retaining aggregation importance without affecting stability. Aggregation and stability can be linked to the influence of much debated magic numbers. Many of our findings can be applied to general hierarchical forecast benchmarking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge