A reinforcement learning guided hybrid evolutionary algorithm for the latency location routing problem

The latency location routing problem integrates the facility location problem and the multi-depot cumulative capacitated vehicle routing problem. This problem involves making simultaneous decisions about depot locations and vehicle routes to serve customers while aiming to minimize the sum of waiting (arriving) times for all customers. To address this computationally challenging problem, we propose a reinforcement learning guided hybrid evolutionary algorithm following the framework of the memetic algorithm. The proposed algorithm relies on a diversity-enhanced multi-parent edge assembly crossover to build promising offspring and a reinforcement learning guided variable neighborhood descent to determine the exploration order of multiple neighborhoods. Additionally, strategic oscillation is used to achieve a balanced exploration of both feasible and infeasible solutions. The competitiveness of the algorithm against state-of-the-art methods is demonstrated by experimental results on the three sets of 76 popular instances, including 51 improved best solutions (new upper bounds) for the 59 instances with unknown optima and equal best results for the remaining instances. We also conduct additional experiments to shed light on the key components of the algorithm.

A Multi-population Integrated Approach for Capacitated Location Routing

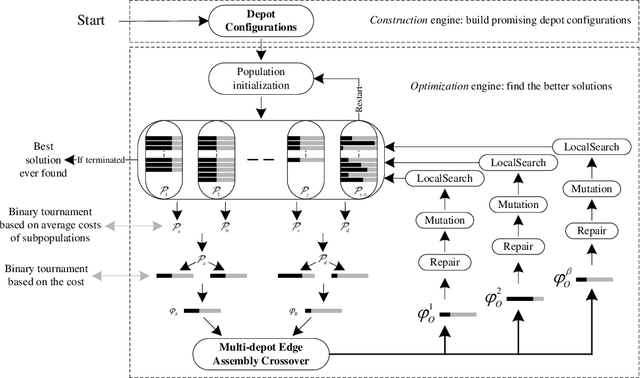
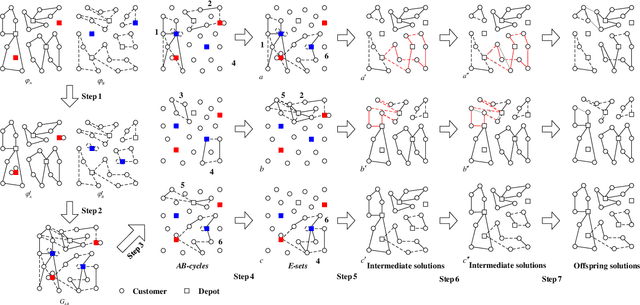
The capacitated location-routing problem involves determining the depots from a set of candidate capacitated depot locations and finding the required routes from the selected depots to serve a set of customers whereas minimizing a cost function that includes the cost of opening the chosen depots, the fixed utilization cost per vehicle used, and the total cost (distance) of the routes. This paper presents a multi-population integrated framework in which a multi-depot edge assembly crossover generates promising offspring solutions from the perspective of both depot location and route edge assembly. The method includes an effective neighborhood-based local search, a feasibility-restoring procedure and a diversification-oriented mutation. Of particular interest is the multi-population scheme which organizes the population into multiple subpopulations based on depot configurations. Extensive experiments on 281 benchmark instances from the literature show that the algorithm performs remarkably well, by improving 101 best-known results (new upper bounds) and matching 84 best-known results. Additional experiments are presented to gain insight into the role of the key elements of the algorithm.

Effective and Differentiated Use of Control Information for Multi-speaker Speech Synthesis

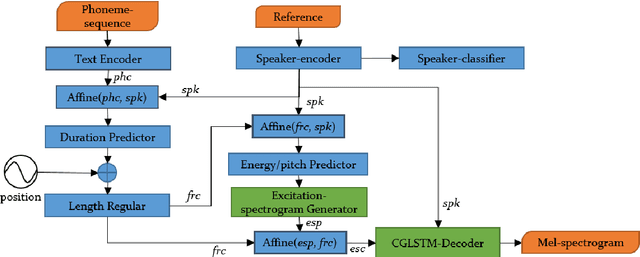
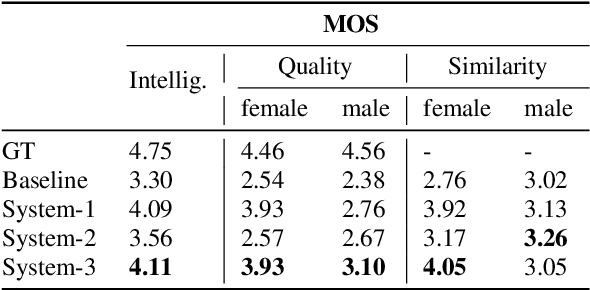
In multi-speaker speech synthesis, data from a number of speakers usually tends to have great diversity due to the fact that the speakers may differ largely in their ages, speaking styles, speeds, emotions, and so on. The diversity of data will lead to the one-to-many mapping problem \cite{Ren2020FastSpeech2F, Kumar2020FewSA}. It is important but challenging to improve the modeling capabilities for multi-speaker speech synthesis. To address the issue, this paper researches into the effective use of control information such as speaker and pitch which are differentiated from text-content information in our encoder-decoder framework: 1) Design a representation of harmonic structure of speech, called excitation spectrogram, from pitch and energy. The excitation spectrogrom is, along with the text-content, fed to the decoder to guide the learning of harmonics of mel-spectrogram. 2) Propose conditional gated LSTM (CGLSTM) whose input/output/forget gates are re-weighted by speaker embedding to control the flow of text-content information in the network. The experiments show significant reduction in reconstruction errors of mel-spectrogram in the training of multi-speaker generative model, and a great improvement is observed in the subjective evaluation of speaker adapted model, e.g, the Mean Opinion Score (MOS) of intelligibility increases by 0.81 points.

Solving the Clustered Traveling Salesman Problem via TSP methods

The Clustered Traveling Salesman Problem (CTSP) is a variant of the popular Traveling Salesman Problem (TSP) arising from a number of real-life applications. In this work, we explore an uncharted solution approach that solves the CTSP by transforming it to the well-studied TSP. For this purpose, we first investigate a technique to convert a CTSP instance to a TSP and then apply popular TSP solvers (including exact and heuristic solvers) to solve the resulting TSP instance. We want to answer the following questions: How do state-of-the-art TSP solvers perform on clustered instances converted from the CTSP? Do state-of-the-art TSP solvers compete well with the best performing methods specifically designed for the CTSP? For this purpose, we present intensive computational experiments on various CTSP benchmark instances to draw conclusions.