Enhancing Mixup-based Semi-Supervised Learning with Explicit Lipschitz Regularization

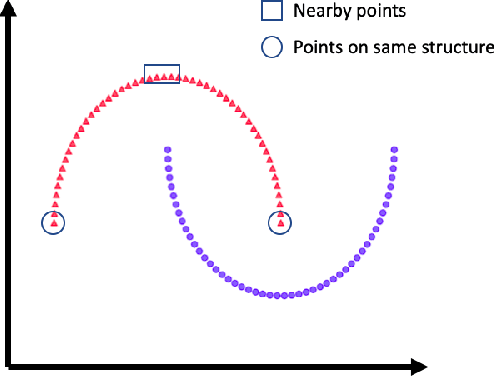
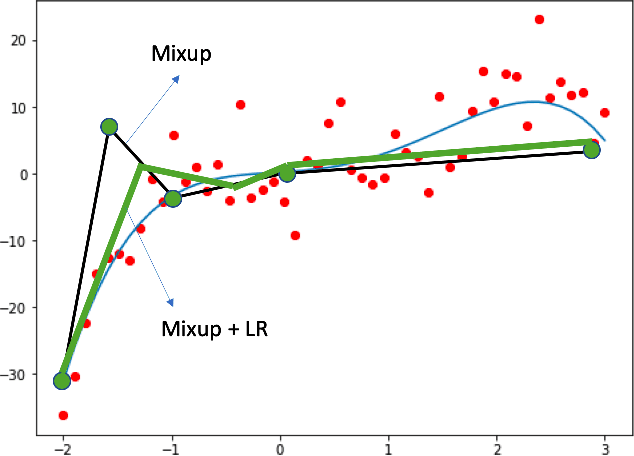
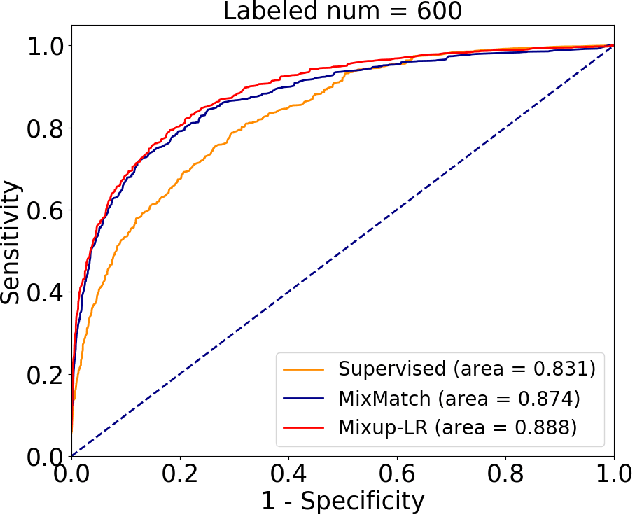
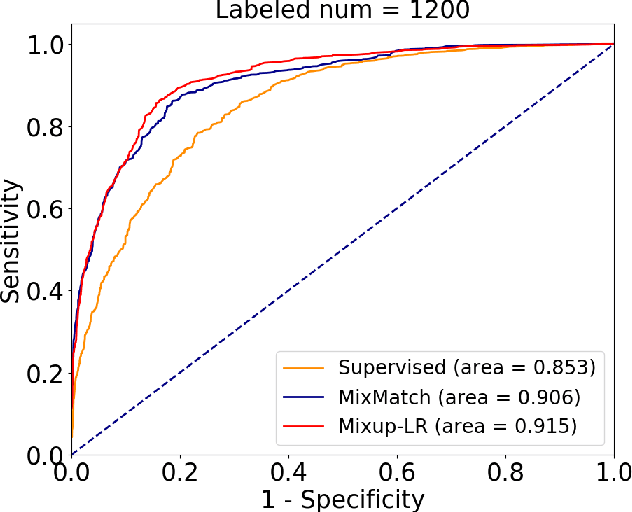
The success of deep learning relies on the availability of large-scale annotated data sets, the acquisition of which can be costly, requiring expert domain knowledge. Semi-supervised learning (SSL) mitigates this challenge by exploiting the behavior of the neural function on large unlabeled data. The smoothness of the neural function is a commonly used assumption exploited in SSL. A successful example is the adoption of mixup strategy in SSL that enforces the global smoothness of the neural function by encouraging it to behave linearly when interpolating between training examples. Despite its empirical success, however, the theoretical underpinning of how mixup regularizes the neural function has not been fully understood. In this paper, we offer a theoretically substantiated proposition that mixup improves the smoothness of the neural function by bounding the Lipschitz constant of the gradient function of the neural networks. We then propose that this can be strengthened by simultaneously constraining the Lipschitz constant of the neural function itself through adversarial Lipschitz regularization, encouraging the neural function to behave linearly while also constraining the slope of this linear function. On three benchmark data sets and one real-world biomedical data set, we demonstrate that this combined regularization results in improved generalization performance of SSL when learning from a small amount of labeled data. We further demonstrate the robustness of the presented method against single-step adversarial attacks. Our code is available at https://github.com/Prasanna1991/Mixup-LR.

Learning Geometry-Dependent and Physics-Based Inverse Image Reconstruction

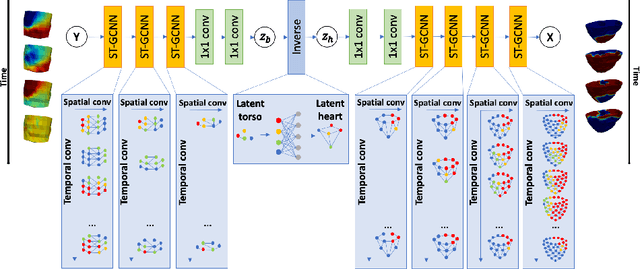
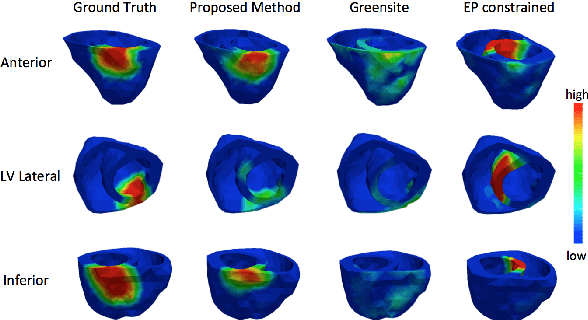
Deep neural networks have shown great potential in image reconstruction problems in Euclidean space. However, many reconstruction problems involve imaging physics that are dependent on the underlying non-Euclidean geometry. In this paper, we present a new approach to learn inverse imaging that exploit the underlying geometry and physics. We first introduce a non-Euclidean encoding-decoding network that allows us to describe the unknown and measurement variables over their respective geometrical domains. We then learn the geometry-dependent physics in between the two domains by explicitly modeling it via a bipartite graph over the graphical embedding of the two geometry. We applied the presented network to reconstructing electrical activity on the heart surface from body-surface potential. In a series of generalization tasks with increasing difficulty, we demonstrated the improved ability of the presented network to generalize across geometrical changes underlying the data in comparison to its Euclidean alternatives.

Semi-supervised Medical Image Classification with Global Latent Mixing

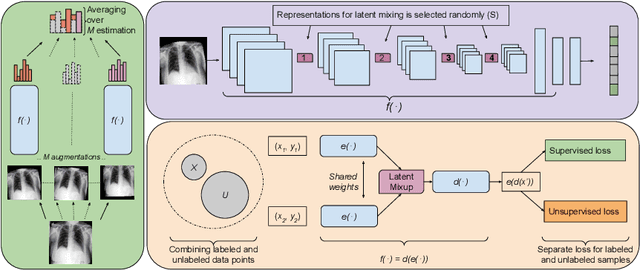
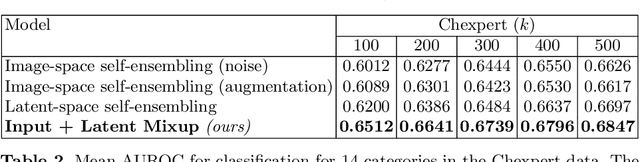
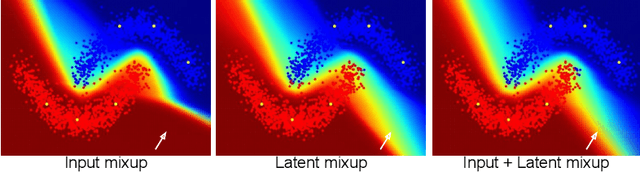
Computer-aided diagnosis via deep learning relies on large-scale annotated data sets, which can be costly when involving expert knowledge. Semi-supervised learning (SSL) mitigates this challenge by leveraging unlabeled data. One effective SSL approach is to regularize the local smoothness of neural functions via perturbations around single data points. In this work, we argue that regularizing the global smoothness of neural functions by filling the void in between data points can further improve SSL. We present a novel SSL approach that trains the neural network on linear mixing of labeled and unlabeled data, at both the input and latent space in order to regularize different portions of the network. We evaluated the presented model on two distinct medical image data sets for semi-supervised classification of thoracic disease and skin lesion, demonstrating its improved performance over SSL with local perturbations and SSL with global mixing but at the input space only. Our code is available at https://github.com/Prasanna1991/LatentMixing.

Progressive Learning and Disentanglement of Hierarchical Representations

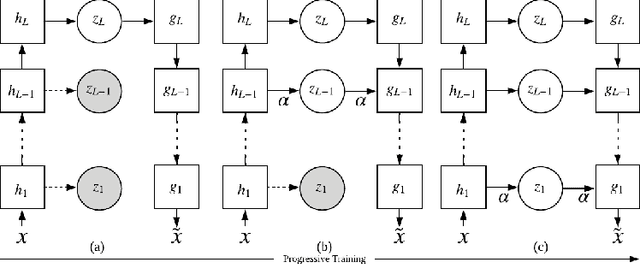
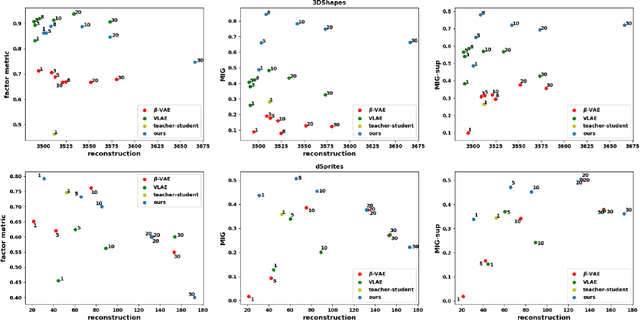
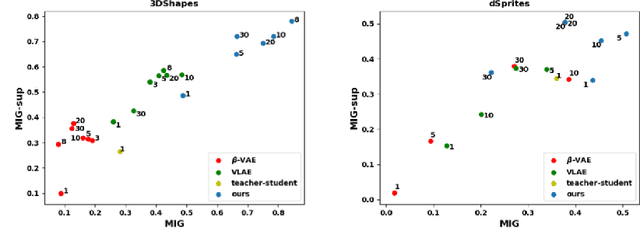
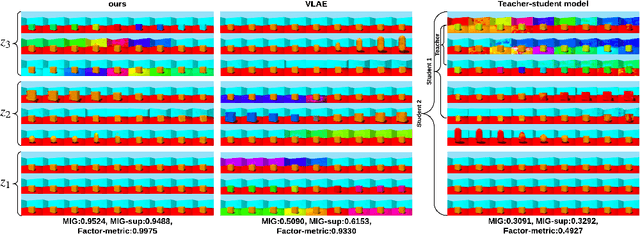
Learning rich representation from data is an important task for deep generative models such as variational auto-encoder (VAE). However, by extracting high-level abstractions in the bottom-up inference process, the goal of preserving all factors of variations for top-down generation is compromised. Motivated by the concept of "starting small", we present a strategy to progressively learn independent hierarchical representations from high- to low-levels of abstractions. The model starts with learning the most abstract representation, and then progressively grow the network architecture to introduce new representations at different levels of abstraction. We quantitatively demonstrate the ability of the presented model to improve disentanglement in comparison to existing works on two benchmark data sets using three disentanglement metrics, including a new metric we proposed to complement the previously-presented metric of mutual information gap. We further present both qualitative and quantitative evidence on how the progression of learning improves disentangling of hierarchical representations. By drawing on the respective advantage of hierarchical representation learning and progressive learning, this is to our knowledge the first attempt to improve disentanglement by progressively growing the capacity of VAE to learn hierarchical representations.

Improving Disentangled Representation Learning with the Beta Bernoulli Process

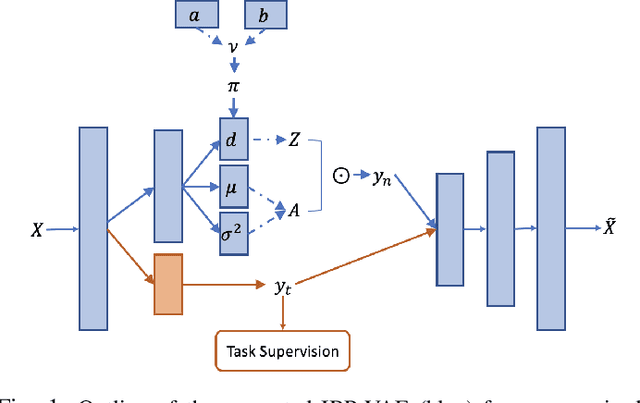
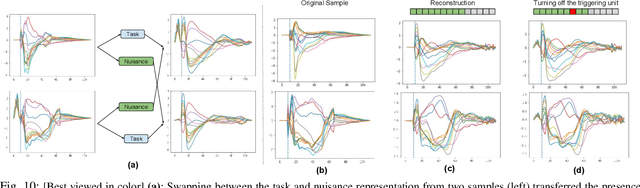
To improve the ability of VAE to disentangle in the latent space, existing works mostly focus on enforcing independence among the learned latent factors. However, the ability of these models to disentangle often decreases as the complexity of the generative factors increases. In this paper, we investigate the little-explored effect of the modeling capacity of a posterior density on the disentangling ability of the VAE. We note that the independence within and the complexity of the latent density are two different properties we constrain when regularizing the posterior density: while the former promotes the disentangling ability of VAE, the latter -- if overly limited -- creates an unnecessary competition with the data reconstruction objective in VAE. Therefore, if we preserve the independence but allow richer modeling capacity in the posterior density, we will lift this competition and thereby allow improved independence and data reconstruction at the same time. We investigate this theoretical intuition with a VAE that utilizes a non-parametric latent factor model, the Indian Buffet Process (IBP), as a latent density that is able to grow with the complexity of the data. Across three widely-used benchmark data sets and two clinical data sets little explored for disentangled learning, we qualitatively and quantitatively demonstrated the improved disentangling performance of IBP-VAE over the state of the art. In the latter two clinical data sets riddled with complex factors of variations, we further demonstrated that unsupervised disentangling of nuisance factors via IBP-VAE -- when combined with a supervised objective -- can not only improve task accuracy in comparison to relevant supervised deep architectures but also facilitate knowledge discovery related to task decision-making. A shorter version of this work will appear in the ICDM 2019 conference proceedings.

Semi-Supervised Learning by Disentangling and Self-Ensembling Over Stochastic Latent Space

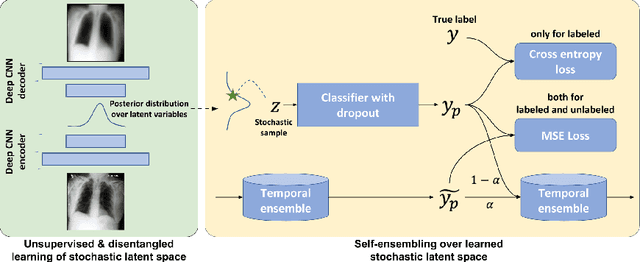
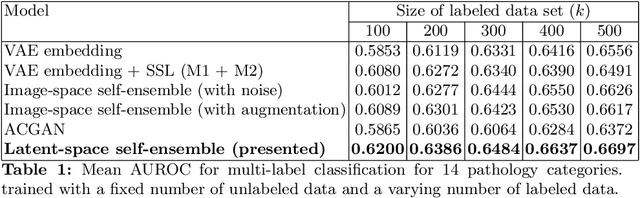
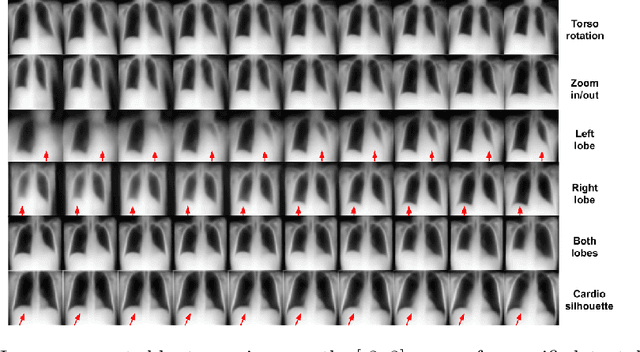
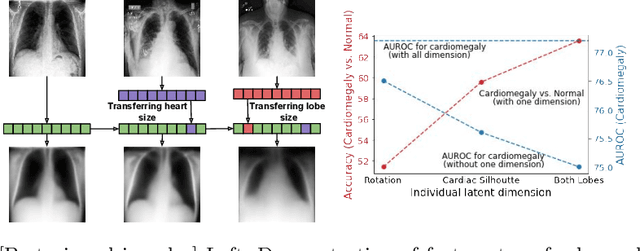
The success of deep learning in medical imaging is mostly achieved at the cost of a large labeled data set. Semi-supervised learning (SSL) provides a promising solution by leveraging the structure of unlabeled data to improve learning from a small set of labeled data. Self-ensembling is a simple approach used in SSL to encourage consensus among ensemble predictions of unknown labels, improving generalization of the model by making it more insensitive to the latent space. Currently, such an ensemble is obtained by randomization such as dropout regularization and random data augmentation. In this work, we hypothesize -- from the generalization perspective -- that self-ensembling can be improved by exploiting the stochasticity of a disentangled latent space. To this end, we present a stacked SSL model that utilizes unsupervised disentangled representation learning as the stochastic embedding for self-ensembling. We evaluate the presented model for multi-label classification using chest X-ray images, demonstrating its improved performance over related SSL models as well as the interpretability of its disentangled representations.

Generative Modeling and Inverse Imaging of Cardiac Transmembrane Potential

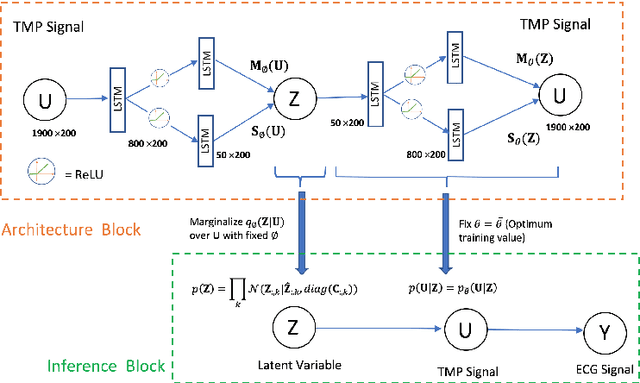
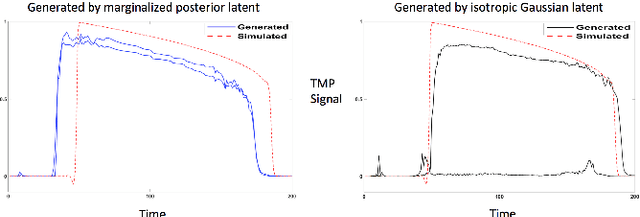
Noninvasive reconstruction of cardiac transmembrane potential (TMP) from surface electrocardiograms (ECG) involves an ill-posed inverse problem. Model-constrained regularization is powerful for incorporating rich physiological knowledge about spatiotemporal TMP dynamics. These models are controlled by high-dimensional physical parameters which, if fixed, can introduce model errors and reduce the accuracy of TMP reconstruction. Simultaneous adaptation of these parameters during TMP reconstruction, however, is difficult due to their high dimensionality. We introduce a novel model-constrained inference framework that replaces conventional physiological models with a deep generative model trained to generate TMP sequences from low-dimensional generative factors. Using a variational auto-encoder (VAE) with long short-term memory (LSTM) networks, we train the VAE decoder to learn the conditional likelihood of TMP, while the encoder learns the prior distribution of generative factors. These two components allow us to develop an efficient algorithm to simultaneously infer the generative factors and TMP signals from ECG data. Synthetic and real-data experiments demonstrate that the presented method significantly improve the accuracy of TMP reconstruction compared with methods constrained by conventional physiological models or without physiological constraints.

Improving Generalization of Deep Networks for Inverse Reconstruction of Image Sequences

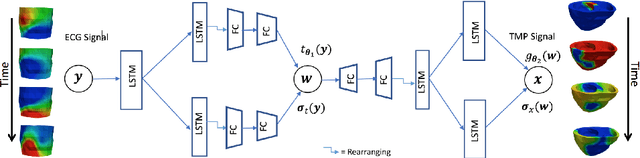
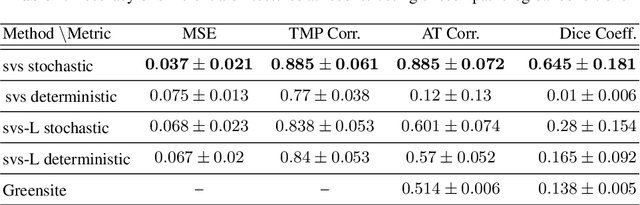
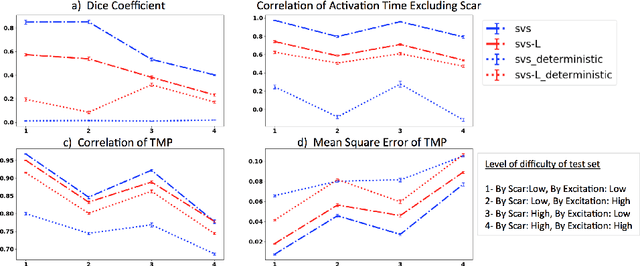
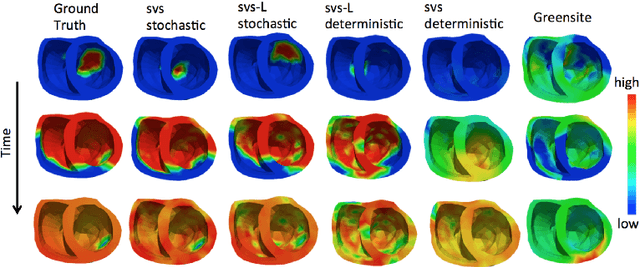
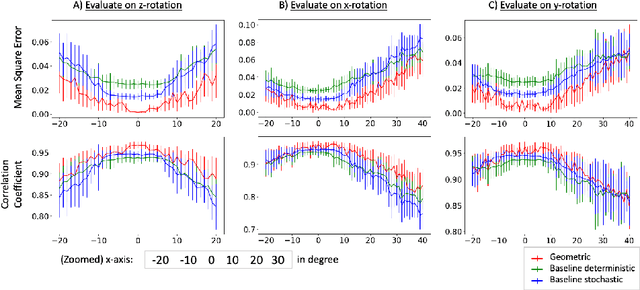
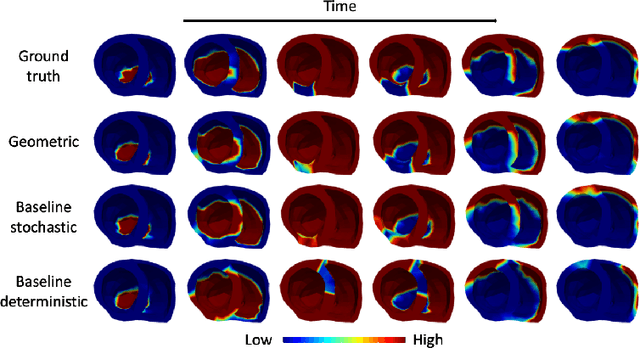
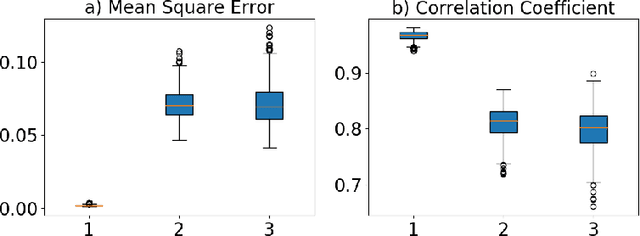
Deep learning networks have shown state-of-the-art performance in many image reconstruction problems. However, it is not well understood what properties of representation and learning may improve the generalization ability of the network. In this paper, we propose that the generalization ability of an encoder-decoder network for inverse reconstruction can be improved in two means. First, drawing from analytical learning theory, we theoretically show that a stochastic latent space will improve the ability of a network to generalize to test data outside the training distribution. Second, following the information bottleneck principle, we show that a latent representation minimally informative of the input data will help a network generalize to unseen input variations that are irrelevant to the output reconstruction. Therefore, we present a sequence image reconstruction network optimized by a variational approximation of the information bottleneck principle with stochastic latent space. In the application setting of reconstructing the sequence of cardiac transmembrane potential from bodysurface potential, we assess the two types of generalization abilities of the presented network against its deterministic counterpart. The results demonstrate that the generalization ability of an inverse reconstruction network can be improved by stochasticity as well as the information bottleneck.

Improving Generalization of Sequence Encoder-Decoder Networks for Inverse Imaging of Cardiac Transmembrane Potential

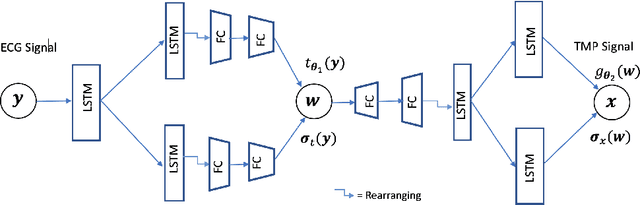
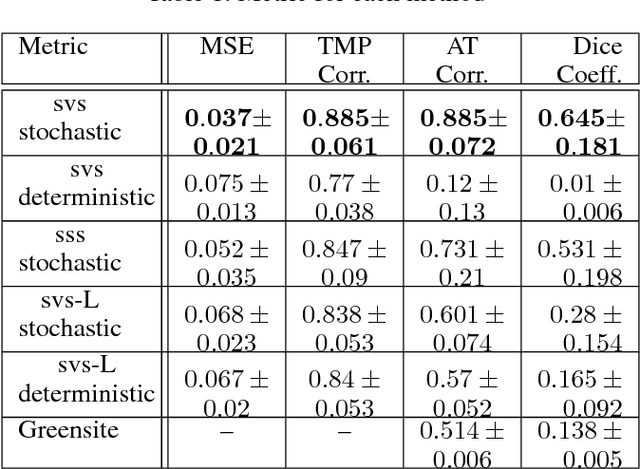
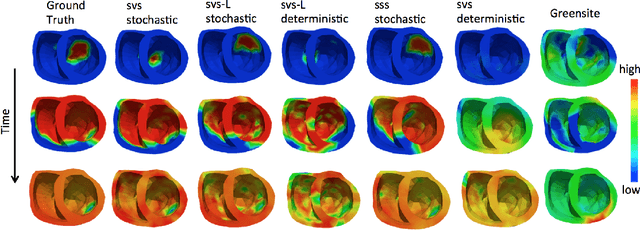
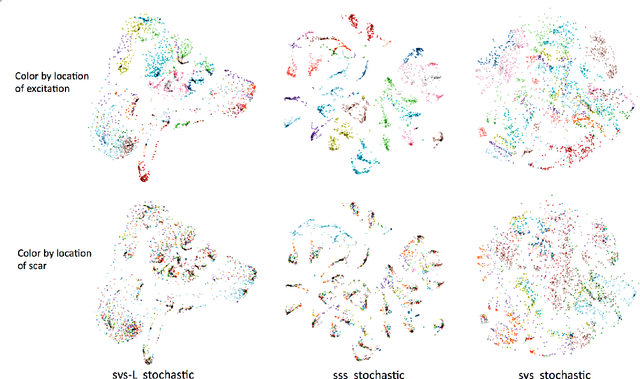
Deep learning models have shown state-of-the-art performance in many inverse reconstruction problems. However, it is not well understood what properties of the latent representation may improve the generalization ability of the network. Furthermore, limited models have been presented for inverse reconstructions over time sequences. In this paper, we study the generalization ability of a sequence encoder decoder model for solving inverse reconstructions on time sequences. Our central hypothesis is that the generalization ability of the network can be improved by 1) constrained stochasticity and 2) global aggregation of temporal information in the latent space. First, drawing from analytical learning theory, we theoretically show that a stochastic latent space will lead to an improved generalization ability. Second, we consider an LSTM encoder-decoder architecture that compresses a global latent vector from all last-layer units in the LSTM encoder. This model is compared with alternative LSTM encoder-decoder architectures, each in deterministic and stochastic versions. The results demonstrate that the generalization ability of an inverse reconstruction network can be improved by constrained stochasticity combined with global aggregation of temporal information in the latent space.