Generative Modeling and Inverse Imaging of Cardiac Transmembrane Potential

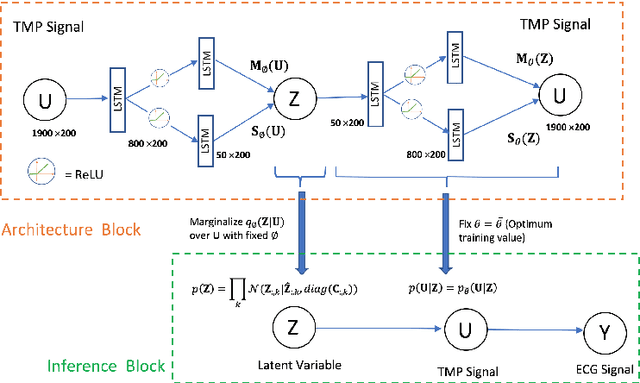
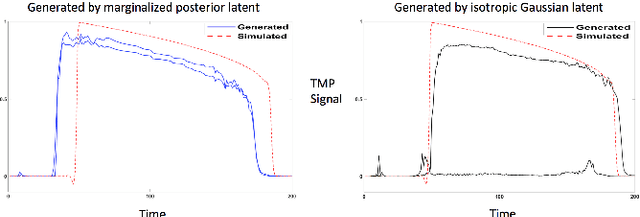
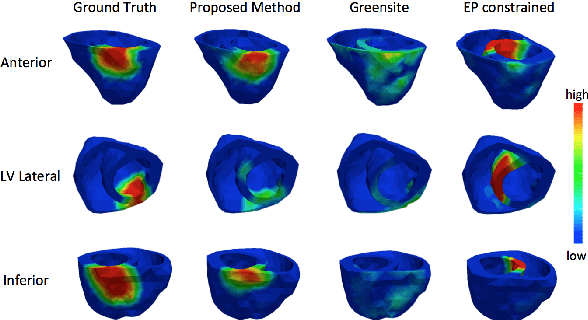
Noninvasive reconstruction of cardiac transmembrane potential (TMP) from surface electrocardiograms (ECG) involves an ill-posed inverse problem. Model-constrained regularization is powerful for incorporating rich physiological knowledge about spatiotemporal TMP dynamics. These models are controlled by high-dimensional physical parameters which, if fixed, can introduce model errors and reduce the accuracy of TMP reconstruction. Simultaneous adaptation of these parameters during TMP reconstruction, however, is difficult due to their high dimensionality. We introduce a novel model-constrained inference framework that replaces conventional physiological models with a deep generative model trained to generate TMP sequences from low-dimensional generative factors. Using a variational auto-encoder (VAE) with long short-term memory (LSTM) networks, we train the VAE decoder to learn the conditional likelihood of TMP, while the encoder learns the prior distribution of generative factors. These two components allow us to develop an efficient algorithm to simultaneously infer the generative factors and TMP signals from ECG data. Synthetic and real-data experiments demonstrate that the presented method significantly improve the accuracy of TMP reconstruction compared with methods constrained by conventional physiological models or without physiological constraints.

Improving Generalization of Deep Networks for Inverse Reconstruction of Image Sequences

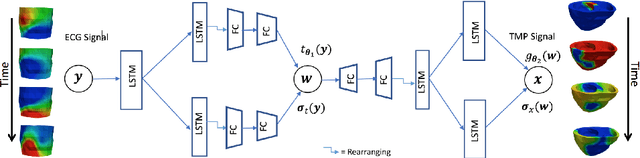
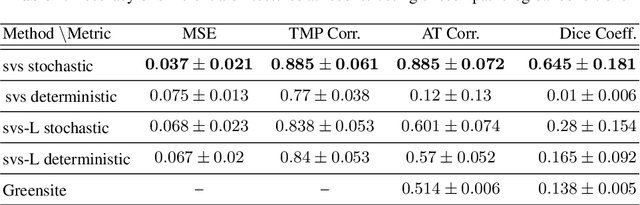
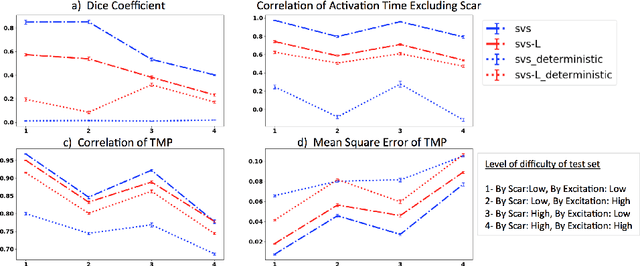
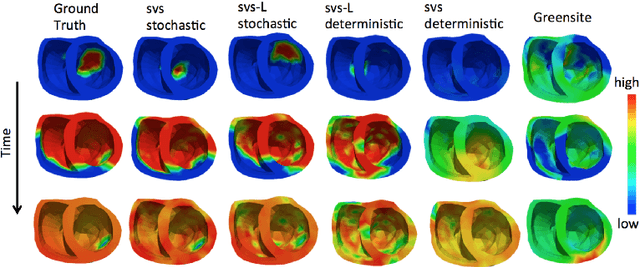
Deep learning networks have shown state-of-the-art performance in many image reconstruction problems. However, it is not well understood what properties of representation and learning may improve the generalization ability of the network. In this paper, we propose that the generalization ability of an encoder-decoder network for inverse reconstruction can be improved in two means. First, drawing from analytical learning theory, we theoretically show that a stochastic latent space will improve the ability of a network to generalize to test data outside the training distribution. Second, following the information bottleneck principle, we show that a latent representation minimally informative of the input data will help a network generalize to unseen input variations that are irrelevant to the output reconstruction. Therefore, we present a sequence image reconstruction network optimized by a variational approximation of the information bottleneck principle with stochastic latent space. In the application setting of reconstructing the sequence of cardiac transmembrane potential from bodysurface potential, we assess the two types of generalization abilities of the presented network against its deterministic counterpart. The results demonstrate that the generalization ability of an inverse reconstruction network can be improved by stochasticity as well as the information bottleneck.

Improving Generalization of Sequence Encoder-Decoder Networks for Inverse Imaging of Cardiac Transmembrane Potential

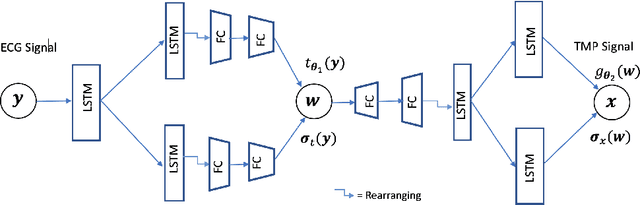
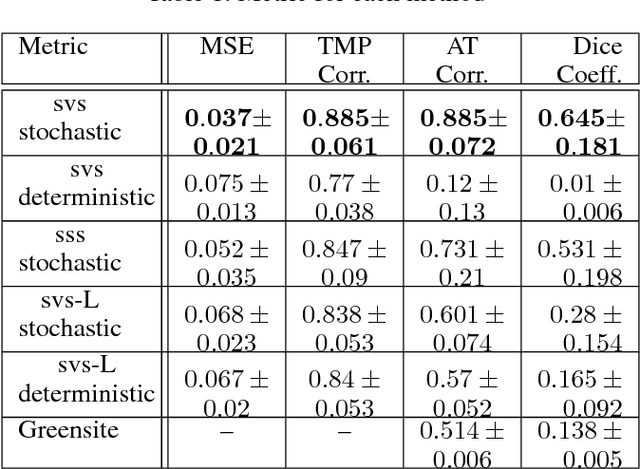
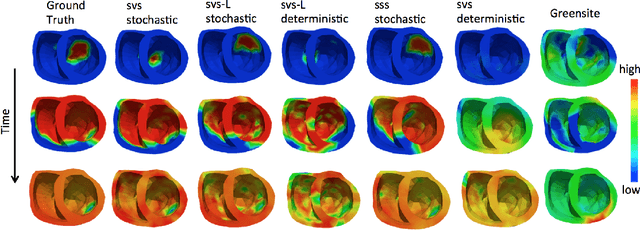
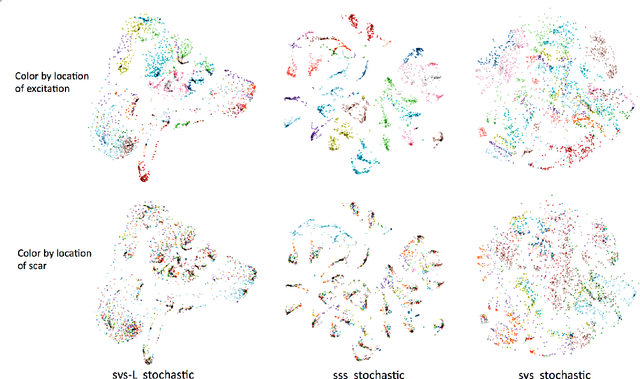
Deep learning models have shown state-of-the-art performance in many inverse reconstruction problems. However, it is not well understood what properties of the latent representation may improve the generalization ability of the network. Furthermore, limited models have been presented for inverse reconstructions over time sequences. In this paper, we study the generalization ability of a sequence encoder decoder model for solving inverse reconstructions on time sequences. Our central hypothesis is that the generalization ability of the network can be improved by 1) constrained stochasticity and 2) global aggregation of temporal information in the latent space. First, drawing from analytical learning theory, we theoretically show that a stochastic latent space will lead to an improved generalization ability. Second, we consider an LSTM encoder-decoder architecture that compresses a global latent vector from all last-layer units in the LSTM encoder. This model is compared with alternative LSTM encoder-decoder architectures, each in deterministic and stochastic versions. The results demonstrate that the generalization ability of an inverse reconstruction network can be improved by constrained stochasticity combined with global aggregation of temporal information in the latent space.