Learning Geometry-Dependent and Physics-Based Inverse Image Reconstruction
Paper and Code
Jul 18, 2020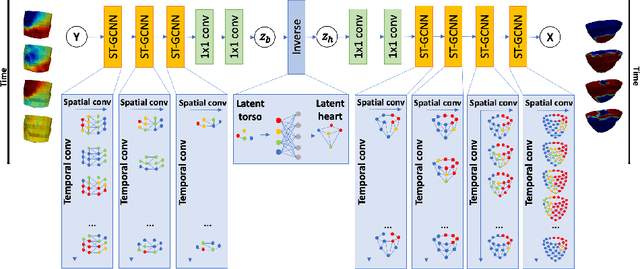
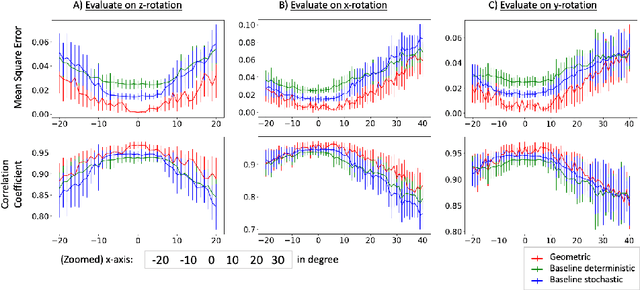
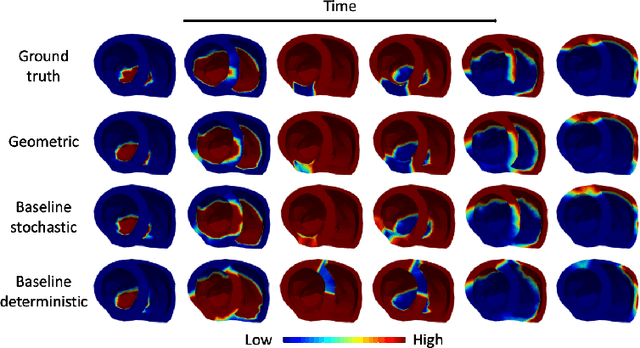
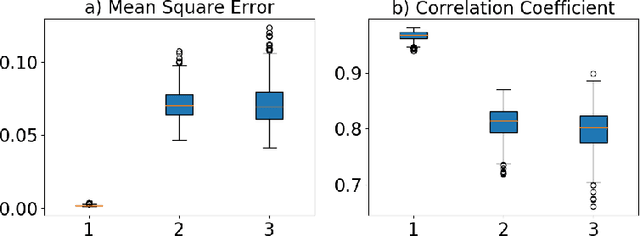
Deep neural networks have shown great potential in image reconstruction problems in Euclidean space. However, many reconstruction problems involve imaging physics that are dependent on the underlying non-Euclidean geometry. In this paper, we present a new approach to learn inverse imaging that exploit the underlying geometry and physics. We first introduce a non-Euclidean encoding-decoding network that allows us to describe the unknown and measurement variables over their respective geometrical domains. We then learn the geometry-dependent physics in between the two domains by explicitly modeling it via a bipartite graph over the graphical embedding of the two geometry. We applied the presented network to reconstructing electrical activity on the heart surface from body-surface potential. In a series of generalization tasks with increasing difficulty, we demonstrated the improved ability of the presented network to generalize across geometrical changes underlying the data in comparison to its Euclidean alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge