A Comprehensive Sustainable Framework for Machine Learning and Artificial Intelligence

In financial applications, regulations or best practices often lead to specific requirements in machine learning relating to four key pillars: fairness, privacy, interpretability and greenhouse gas emissions. These all sit in the broader context of sustainability in AI, an emerging practical AI topic. However, although these pillars have been individually addressed by past literature, none of these works have considered all the pillars. There are inherent trade-offs between each of the pillars (for example, accuracy vs fairness or accuracy vs privacy), making it even more important to consider them together. This paper outlines a new framework for Sustainable Machine Learning and proposes FPIG, a general AI pipeline that allows for these critical topics to be considered simultaneously to learn the trade-offs between the pillars better. Based on the FPIG framework, we propose a meta-learning algorithm to estimate the four key pillars given a dataset summary, model architecture, and hyperparameters before model training. This algorithm allows users to select the optimal model architecture for a given dataset and a given set of user requirements on the pillars. We illustrate the trade-offs under the FPIG model on three classical datasets and demonstrate the meta-learning approach with an example of real-world datasets and models with different interpretability, showcasing how it can aid model selection.

Private Training Set Inspection in MLaaS

Machine Learning as a Service (MLaaS) is a popular cloud-based solution for customers who aim to use an ML model but lack training data, computation resources, or expertise in ML. In this case, the training datasets are typically a private possession of the ML or data companies and are inaccessible to the customers, but the customers still need an approach to confirm that the training datasets meet their expectations and fulfil regulatory measures like fairness. However, no existing work addresses the above customers' concerns. This work is the first attempt to solve this problem, taking data origin as an entry point. We first define origin membership measurement and based on this, we then define diversity and fairness metrics to address customers' concerns. We then propose a strategy to estimate the values of these two metrics in the inaccessible training dataset, combining shadow training techniques from membership inference and an efficient featurization scheme in multiple instance learning. The evaluation contains an application of text review polarity classification applications based on the language BERT model. Experimental results show that our solution can achieve up to 0.87 accuracy for membership inspection and up to 99.3% confidence in inspecting diversity and fairness distribution.

Learning to Compensate: A Deep Neural Network Framework for 5G Power Amplifier Compensation

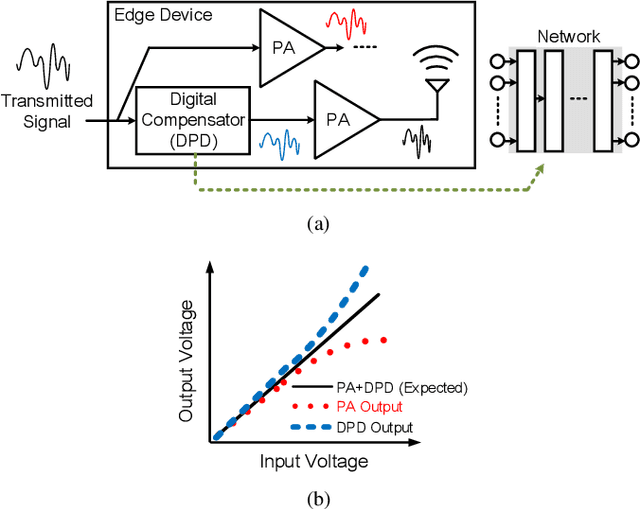
Owing to the complicated characteristics of 5G communication system, designing RF components through mathematical modeling becomes a challenging obstacle. Moreover, such mathematical models need numerous manual adjustments for various specification requirements. In this paper, we present a learning-based framework to model and compensate Power Amplifiers (PAs) in 5G communication. In the proposed framework, Deep Neural Networks (DNNs) are used to learn the characteristics of the PAs, while, correspondent Digital Pre-Distortions (DPDs) are also learned to compensate for the nonlinear and memory effects of PAs. On top of the framework, we further propose two frequency domain losses to guide the learning process to better optimize the target, compared to naive time domain Mean Square Error (MSE). The proposed framework serves as a drop-in replacement for the conventional approach. The proposed approach achieves an average of 56.7% reduction of nonlinear and memory effects, which converts to an average of 16.3% improvement over a carefully-designed mathematical model, and even reaches 34% enhancement in severe distortion scenarios.

Group-Sparse Signal Denoising: Non-Convex Regularization, Convex Optimization

Convex optimization with sparsity-promoting convex regularization is a standard approach for estimating sparse signals in noise. In order to promote sparsity more strongly than convex regularization, it is also standard practice to employ non-convex optimization. In this paper, we take a third approach. We utilize a non-convex regularization term chosen such that the total cost function (consisting of data consistency and regularization terms) is convex. Therefore, sparsity is more strongly promoted than in the standard convex formulation, but without sacrificing the attractive aspects of convex optimization (unique minimum, robust algorithms, etc.). We use this idea to improve the recently developed 'overlapping group shrinkage' (OGS) algorithm for the denoising of group-sparse signals. The algorithm is applied to the problem of speech enhancement with favorable results in terms of both SNR and perceptual quality.

Image Restoration using Total Variation with Overlapping Group Sparsity

Image restoration is one of the most fundamental issues in imaging science. Total variation (TV) regularization is widely used in image restoration problems for its capability to preserve edges. In the literature, however, it is also well known for producing staircase-like artifacts. Usually, the high-order total variation (HTV) regularizer is an good option except its over-smoothing property. In this work, we study a minimization problem where the objective includes an usual $l_2$ data-fidelity term and an overlapping group sparsity total variation regularizer which can avoid staircase effect and allow edges preserving in the restored image. We also proposed a fast algorithm for solving the corresponding minimization problem and compare our method with the state-of-the-art TV based methods and HTV based method. The numerical experiments illustrate the efficiency and effectiveness of the proposed method in terms of PSNR, relative error and computing time.

Translation-Invariant Shrinkage/Thresholding of Group Sparse Signals

This paper addresses signal denoising when large-amplitude coefficients form clusters (groups). The L1-norm and other separable sparsity models do not capture the tendency of coefficients to cluster (group sparsity). This work develops an algorithm, called 'overlapping group shrinkage' (OGS), based on the minimization of a convex cost function involving a group-sparsity promoting penalty function. The groups are fully overlapping so the denoising method is translation-invariant and blocking artifacts are avoided. Based on the principle of majorization-minimization (MM), we derive a simple iterative minimization algorithm that reduces the cost function monotonically. A procedure for setting the regularization parameter, based on attenuating the noise to a specified level, is also described. The proposed approach is illustrated on speech enhancement, wherein the OGS approach is applied in the short-time Fourier transform (STFT) domain. The denoised speech produced by OGS does not suffer from musical noise.