Improved Sparse Low-Rank Matrix Estimation

We address the problem of estimating a sparse low-rank matrix from its noisy observation. We propose an objective function consisting of a data-fidelity term and two parameterized non-convex penalty functions. Further, we show how to set the parameters of the non-convex penalty functions, in order to ensure that the objective function is strictly convex. The proposed objective function better estimates sparse low-rank matrices than a convex method which utilizes the sum of the nuclear norm and the $\ell_1$ norm. We derive an algorithm (as an instance of ADMM) to solve the proposed problem, and guarantee its convergence provided the scalar augmented Lagrangian parameter is set appropriately. We demonstrate the proposed method for denoising an audio signal and an adjacency matrix representing protein interactions in the `Escherichia coli' bacteria.

Enhanced Low-Rank Matrix Approximation

This letter proposes to estimate low-rank matrices by formulating a convex optimization problem with non-convex regularization. We employ parameterized non-convex penalty functions to estimate the non-zero singular values more accurately than the nuclear norm. A closed-form solution for the global optimum of the proposed objective function (sum of data fidelity and the non-convex regularizer) is also derived. The solution reduces to singular value thresholding method as a special case. The proposed method is demonstrated for image denoising.

Sparsity-based Correction of Exponential Artifacts

This paper describes an exponential transient excision algorithm (ETEA). In biomedical time series analysis, e.g., in vivo neural recording and electrocorticography (ECoG), some measurement artifacts take the form of piecewise exponential transients. The proposed method is formulated as an unconstrained convex optimization problem, regularized by smoothed l1-norm penalty function, which can be solved by majorization-minimization (MM) method. With a slight modification of the regularizer, ETEA can also suppress more irregular piecewise smooth artifacts, especially, ocular artifacts (OA) in electroencephalog- raphy (EEG) data. Examples of synthetic signal, EEG data, and ECoG data are presented to illustrate the proposed algorithms.

Convex Denoising using Non-Convex Tight Frame Regularization

This paper considers the problem of signal denoising using a sparse tight-frame analysis prior. The L1 norm has been extensively used as a regularizer to promote sparsity; however, it tends to under-estimate non-zero values of the underlying signal. To more accurately estimate non-zero values, we propose the use of a non-convex regularizer, chosen so as to ensure convexity of the objective function. The convexity of the objective function is ensured by constraining the parameter of the non-convex penalty. We use ADMM to obtain a solution and show how to guarantee that ADMM converges to the global optimum of the objective function. We illustrate the proposed method for 1D and 2D signal denoising.

Sparse Signal Estimation by Maximally Sparse Convex Optimization

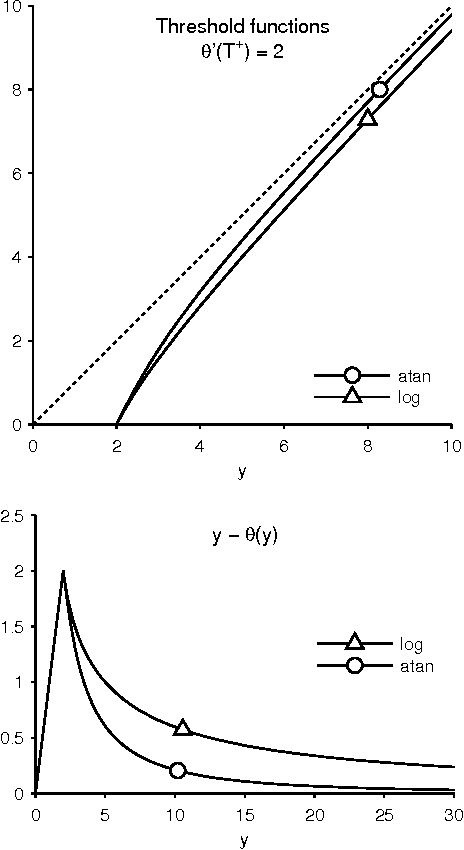
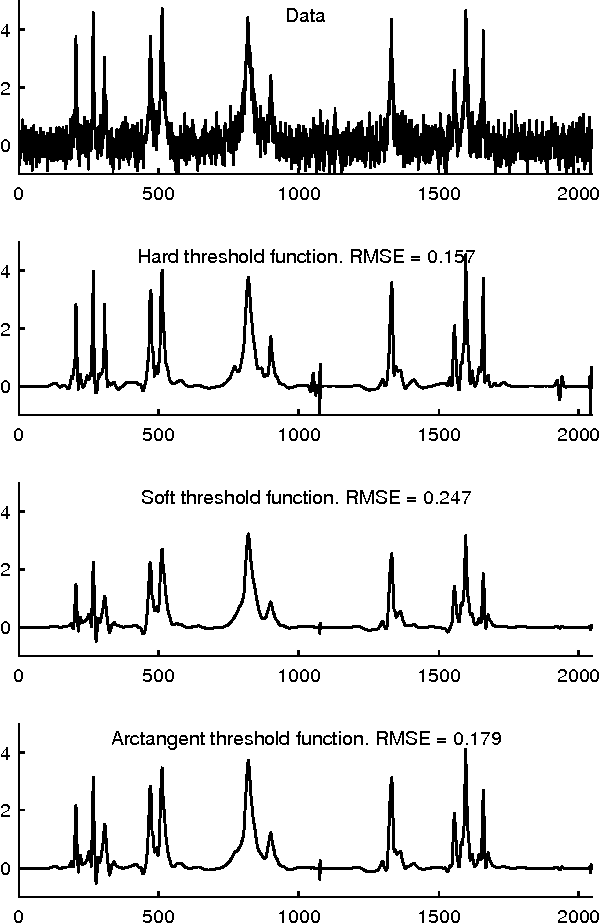
This paper addresses the problem of sparsity penalized least squares for applications in sparse signal processing, e.g. sparse deconvolution. This paper aims to induce sparsity more strongly than L1 norm regularization, while avoiding non-convex optimization. For this purpose, this paper describes the design and use of non-convex penalty functions (regularizers) constrained so as to ensure the convexity of the total cost function, F, to be minimized. The method is based on parametric penalty functions, the parameters of which are constrained to ensure convexity of F. It is shown that optimal parameters can be obtained by semidefinite programming (SDP). This maximally sparse convex (MSC) approach yields maximally non-convex sparsity-inducing penalty functions constrained such that the total cost function, F, is convex. It is demonstrated that iterative MSC (IMSC) can yield solutions substantially more sparse than the standard convex sparsity-inducing approach, i.e., L1 norm minimization.

Group-Sparse Signal Denoising: Non-Convex Regularization, Convex Optimization

Convex optimization with sparsity-promoting convex regularization is a standard approach for estimating sparse signals in noise. In order to promote sparsity more strongly than convex regularization, it is also standard practice to employ non-convex optimization. In this paper, we take a third approach. We utilize a non-convex regularization term chosen such that the total cost function (consisting of data consistency and regularization terms) is convex. Therefore, sparsity is more strongly promoted than in the standard convex formulation, but without sacrificing the attractive aspects of convex optimization (unique minimum, robust algorithms, etc.). We use this idea to improve the recently developed 'overlapping group shrinkage' (OGS) algorithm for the denoising of group-sparse signals. The algorithm is applied to the problem of speech enhancement with favorable results in terms of both SNR and perceptual quality.

Image Restoration using Total Variation with Overlapping Group Sparsity

Image restoration is one of the most fundamental issues in imaging science. Total variation (TV) regularization is widely used in image restoration problems for its capability to preserve edges. In the literature, however, it is also well known for producing staircase-like artifacts. Usually, the high-order total variation (HTV) regularizer is an good option except its over-smoothing property. In this work, we study a minimization problem where the objective includes an usual $l_2$ data-fidelity term and an overlapping group sparsity total variation regularizer which can avoid staircase effect and allow edges preserving in the restored image. We also proposed a fast algorithm for solving the corresponding minimization problem and compare our method with the state-of-the-art TV based methods and HTV based method. The numerical experiments illustrate the efficiency and effectiveness of the proposed method in terms of PSNR, relative error and computing time.

Translation-Invariant Shrinkage/Thresholding of Group Sparse Signals

This paper addresses signal denoising when large-amplitude coefficients form clusters (groups). The L1-norm and other separable sparsity models do not capture the tendency of coefficients to cluster (group sparsity). This work develops an algorithm, called 'overlapping group shrinkage' (OGS), based on the minimization of a convex cost function involving a group-sparsity promoting penalty function. The groups are fully overlapping so the denoising method is translation-invariant and blocking artifacts are avoided. Based on the principle of majorization-minimization (MM), we derive a simple iterative minimization algorithm that reduces the cost function monotonically. A procedure for setting the regularization parameter, based on attenuating the noise to a specified level, is also described. The proposed approach is illustrated on speech enhancement, wherein the OGS approach is applied in the short-time Fourier transform (STFT) domain. The denoised speech produced by OGS does not suffer from musical noise.

Sparse Frequency Analysis with Sparse-Derivative Instantaneous Amplitude and Phase Functions

This paper addresses the problem of expressing a signal as a sum of frequency components (sinusoids) wherein each sinusoid may exhibit abrupt changes in its amplitude and/or phase. The Fourier transform of a narrow-band signal, with a discontinuous amplitude and/or phase function, exhibits spectral and temporal spreading. The proposed method aims to avoid such spreading by explicitly modeling the signal of interest as a sum of sinusoids with time-varying amplitudes. So as to accommodate abrupt changes, it is further assumed that the amplitude/phase functions are approximately piecewise constant (i.e., their time-derivatives are sparse). The proposed method is based on a convex variational (optimization) approach wherein the total variation (TV) of the amplitude functions are regularized subject to a perfect (or approximate) reconstruction constraint. A computationally efficient algorithm is derived based on convex optimization techniques. The proposed technique can be used to perform band-pass filtering that is relatively insensitive to narrow-band amplitude/phase jumps present in data, which normally pose a challenge (due to transients, leakage, etc.). The method is illustrated using both synthetic signals and human EEG data for the purpose of band-pass filtering and the estimation of phase synchrony indexes.