Interbeat Interval Filtering

Interbeat intervals (IBIs) carry heart rate and heartrate variability information. When the IBIs are correct, this information can be extracted through simple statistics such as mean/median/standard deviation. However, more robust approaches are needed especially in ambulatory conditions where the underlying signal can be noisy. In this paper, we propose a lightweight filter that (i) tracks the time-varying distribution of interbeat intervals, (ii) is robust to outliers. The tracked distribution summarizes relevant information of interest and alleviates the need for further analysis. We demonstrate numerically that the tracked distribution can provide more accurate estimates than a two-stage algorithm that first fixes the IBIs before computing the statistics of interest.

Sparse Signal Estimation by Maximally Sparse Convex Optimization

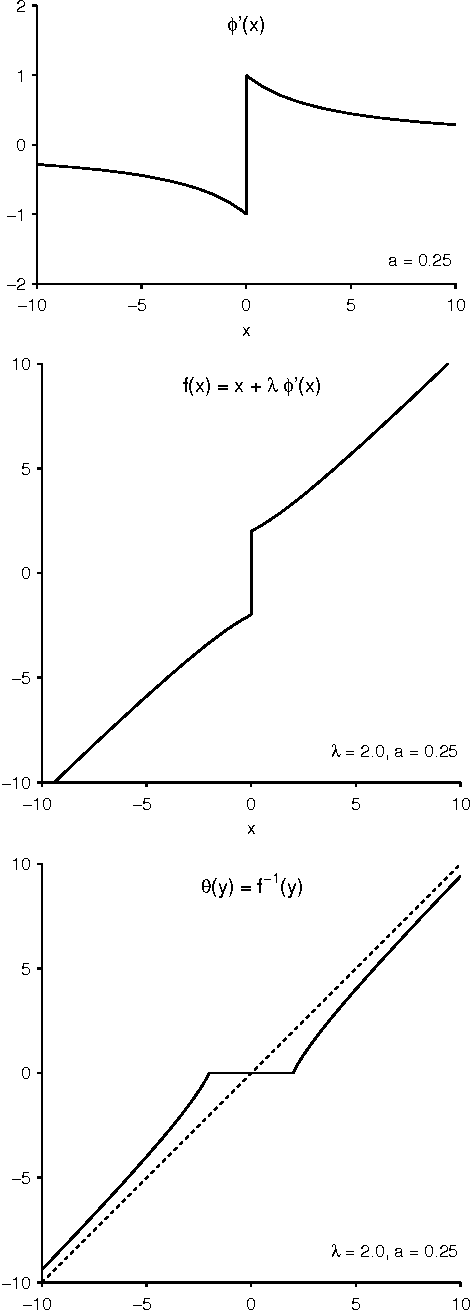
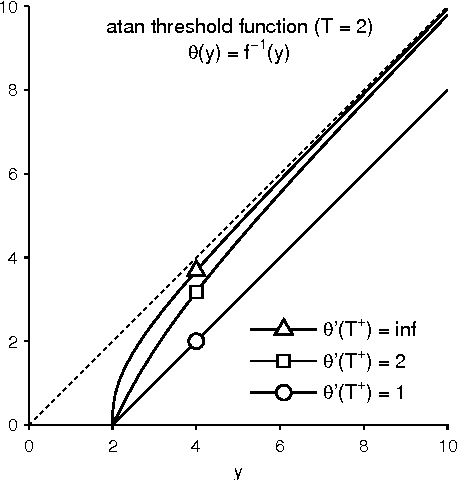
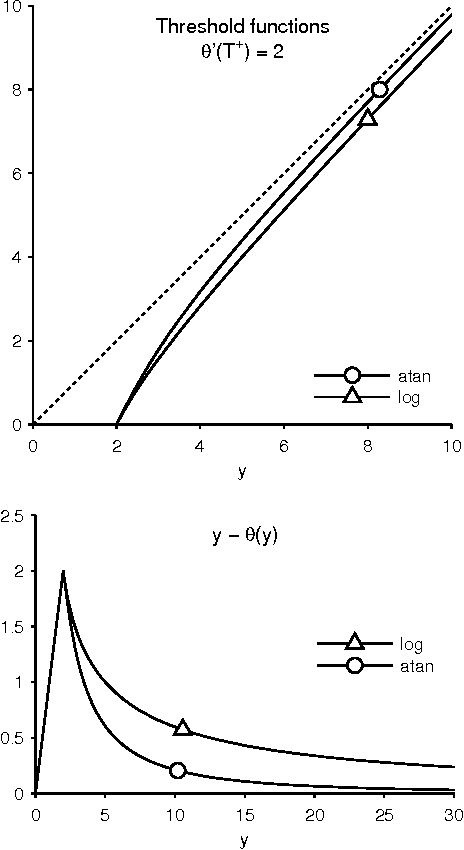
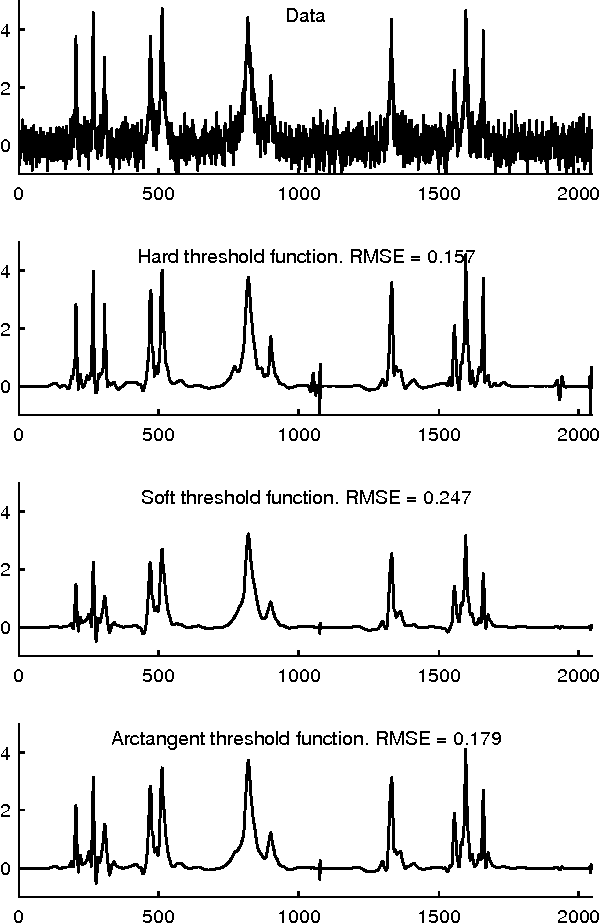
This paper addresses the problem of sparsity penalized least squares for applications in sparse signal processing, e.g. sparse deconvolution. This paper aims to induce sparsity more strongly than L1 norm regularization, while avoiding non-convex optimization. For this purpose, this paper describes the design and use of non-convex penalty functions (regularizers) constrained so as to ensure the convexity of the total cost function, F, to be minimized. The method is based on parametric penalty functions, the parameters of which are constrained to ensure convexity of F. It is shown that optimal parameters can be obtained by semidefinite programming (SDP). This maximally sparse convex (MSC) approach yields maximally non-convex sparsity-inducing penalty functions constrained such that the total cost function, F, is convex. It is demonstrated that iterative MSC (IMSC) can yield solutions substantially more sparse than the standard convex sparsity-inducing approach, i.e., L1 norm minimization.