Piotr Zielinski
Code World Models for General Game Playing
Oct 06, 2025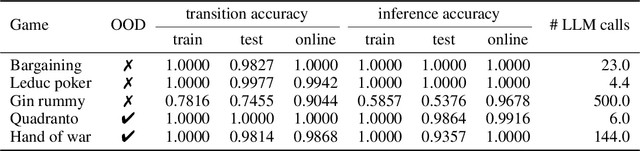

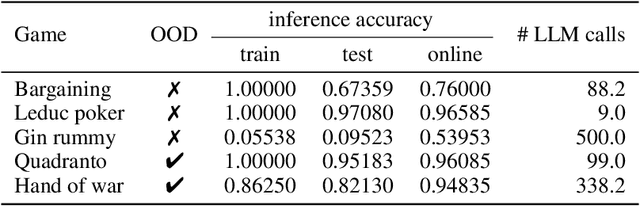
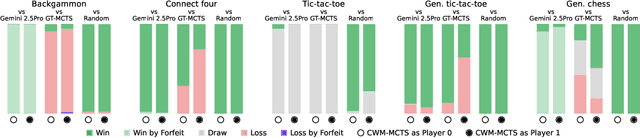
Abstract:Large Language Models (LLMs) reasoning abilities are increasingly being applied to classical board and card games, but the dominant approach -- involving prompting for direct move generation -- has significant drawbacks. It relies on the model's implicit fragile pattern-matching capabilities, leading to frequent illegal moves and strategically shallow play. Here we introduce an alternative approach: We use the LLM to translate natural language rules and game trajectories into a formal, executable world model represented as Python code. This generated model -- comprising functions for state transition, legal move enumeration, and termination checks -- serves as a verifiable simulation engine for high-performance planning algorithms like Monte Carlo tree search (MCTS). In addition, we prompt the LLM to generate heuristic value functions (to make MCTS more efficient), and inference functions (to estimate hidden states in imperfect information games). Our method offers three distinct advantages compared to directly using the LLM as a policy: (1) Verifiability: The generated CWM serves as a formal specification of the game's rules, allowing planners to algorithmically enumerate valid actions and avoid illegal moves, contingent on the correctness of the synthesized model; (2) Strategic Depth: We combine LLM semantic understanding with the deep search power of classical planners; and (3) Generalization: We direct the LLM to focus on the meta-task of data-to-code translation, enabling it to adapt to new games more easily. We evaluate our agent on 10 different games, of which 4 are novel and created for this paper. 5 of the games are fully observed (perfect information), and 5 are partially observed (imperfect information). We find that our method outperforms or matches Gemini 2.5 Pro in 9 out of the 10 considered games.
A Closer Look at Hardware-Friendly Weight Quantization
Oct 07, 2022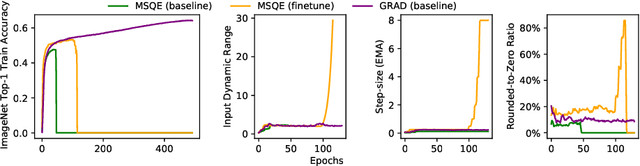
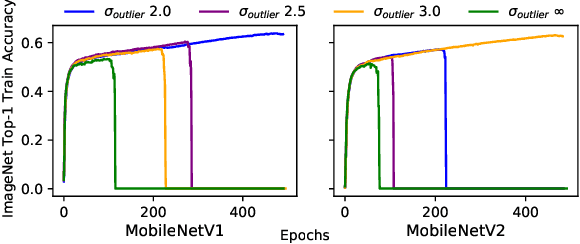
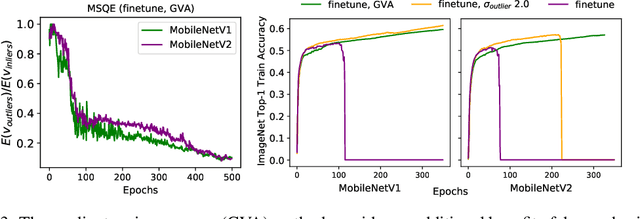
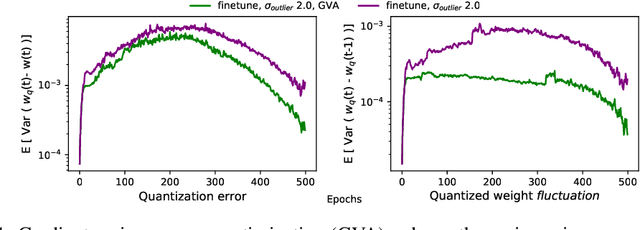
Abstract:Quantizing a Deep Neural Network (DNN) model to be used on a custom accelerator with efficient fixed-point hardware implementations, requires satisfying many stringent hardware-friendly quantization constraints to train the model. We evaluate the two main classes of hardware-friendly quantization methods in the context of weight quantization: the traditional Mean Squared Quantization Error (MSQE)-based methods and the more recent gradient-based methods. We study the two methods on MobileNetV1 and MobileNetV2 using multiple empirical metrics to identify the sources of performance differences between the two classes, namely, sensitivity to outliers and convergence instability of the quantizer scaling factor. Using those insights, we propose various techniques to improve the performance of both quantization methods - they fix the optimization instability issues present in the MSQE-based methods during quantization of MobileNet models and allow us to improve validation performance of the gradient-based methods by 4.0% and 3.3% for MobileNetV1 and MobileNetV2 on ImageNet respectively.
On the Generalization Mystery in Deep Learning
Mar 31, 2022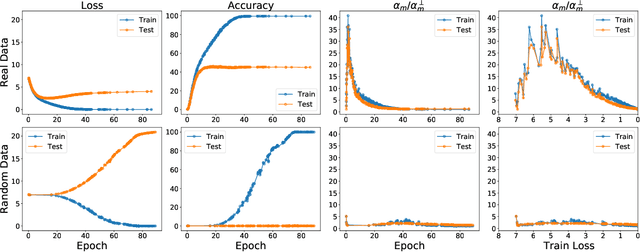
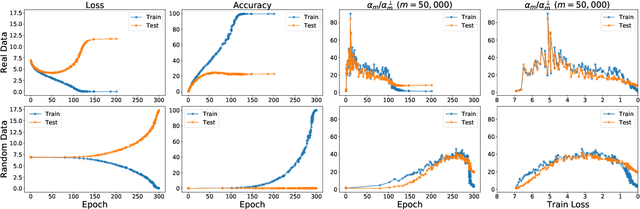
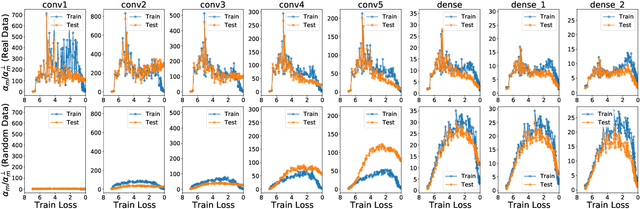
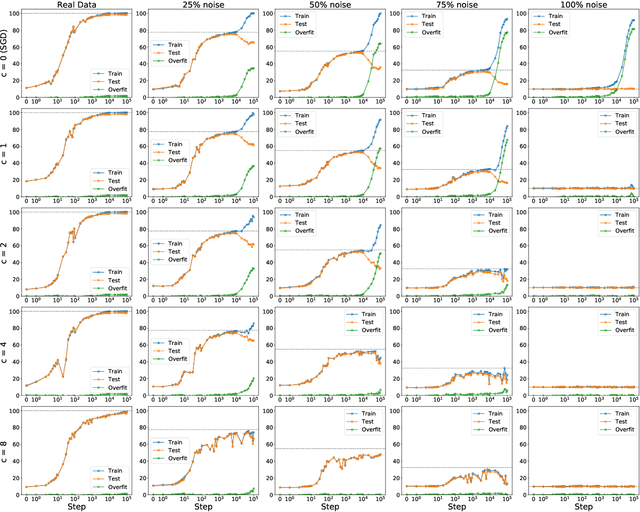
Abstract:The generalization mystery in deep learning is the following: Why do over-parameterized neural networks trained with gradient descent (GD) generalize well on real datasets even though they are capable of fitting random datasets of comparable size? Furthermore, from among all solutions that fit the training data, how does GD find one that generalizes well (when such a well-generalizing solution exists)? We argue that the answer to both questions lies in the interaction of the gradients of different examples during training. Intuitively, if the per-example gradients are well-aligned, that is, if they are coherent, then one may expect GD to be (algorithmically) stable, and hence generalize well. We formalize this argument with an easy to compute and interpretable metric for coherence, and show that the metric takes on very different values on real and random datasets for several common vision networks. The theory also explains a number of other phenomena in deep learning, such as why some examples are reliably learned earlier than others, why early stopping works, and why it is possible to learn from noisy labels. Moreover, since the theory provides a causal explanation of how GD finds a well-generalizing solution when one exists, it motivates a class of simple modifications to GD that attenuate memorization and improve generalization. Generalization in deep learning is an extremely broad phenomenon, and therefore, it requires an equally general explanation. We conclude with a survey of alternative lines of attack on this problem, and argue that the proposed approach is the most viable one on this basis.
Enabling Binary Neural Network Training on the Edge
Feb 10, 2021
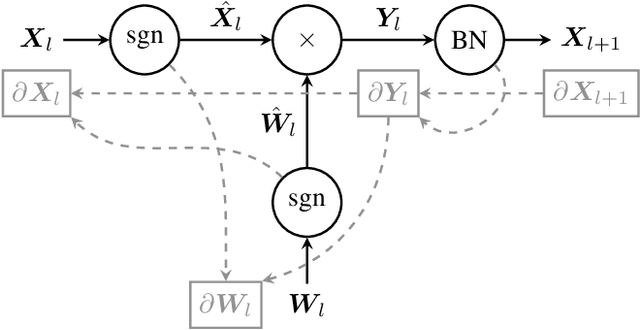
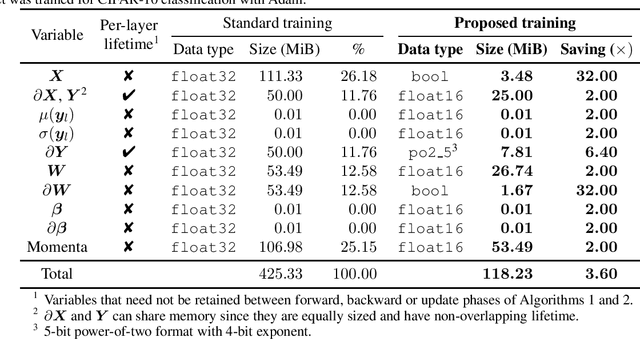
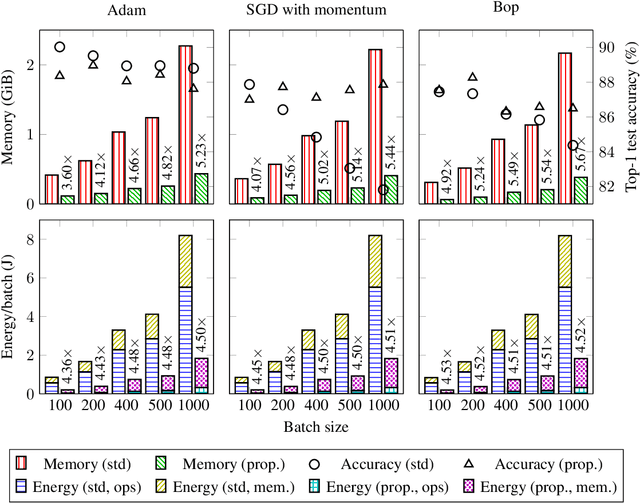
Abstract:The ever-growing computational demands of increasingly complex machine learning models frequently necessitate the use of powerful cloud-based infrastructure for their training. Binary neural networks are known to be promising candidates for on-device inference due to their extreme compute and memory savings over higher-precision alternatives. In this paper, we demonstrate that they are also strongly robust to gradient quantization, thereby making the training of modern models on the edge a practical reality. We introduce a low-cost binary neural network training strategy exhibiting sizable memory footprint reductions and energy savings vs Courbariaux & Bengio's standard approach. Against the latter, we see coincident memory requirement and energy consumption drops of 2--6$\times$, while reaching similar test accuracy in comparable time, across a range of small-scale models trained to classify popular datasets. We also showcase ImageNet training of ResNetE-18, achieving a 3.12$\times$ memory reduction over the aforementioned standard. Such savings will allow for unnecessary cloud offloading to be avoided, reducing latency, increasing energy efficiency and safeguarding privacy.
Making Coherence Out of Nothing At All: Measuring the Evolution of Gradient Alignment
Aug 03, 2020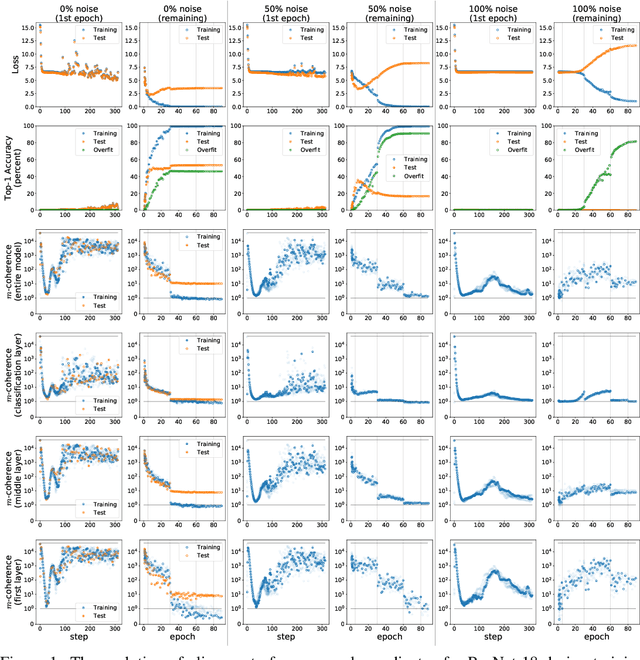
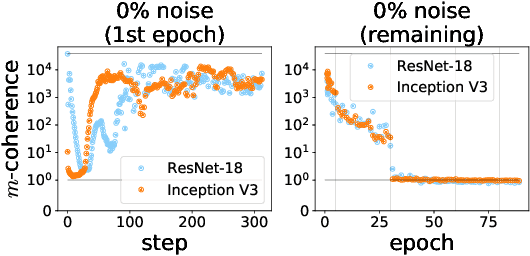
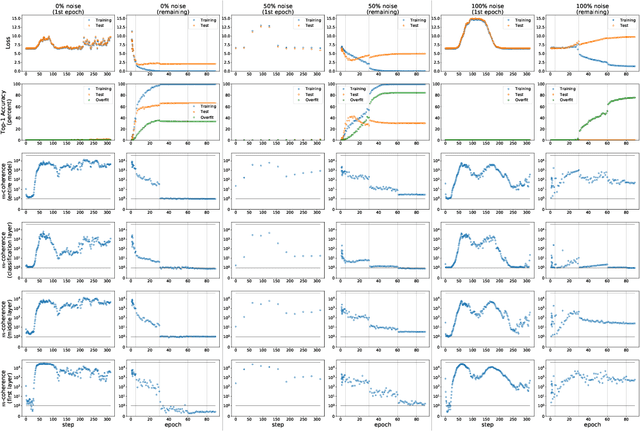
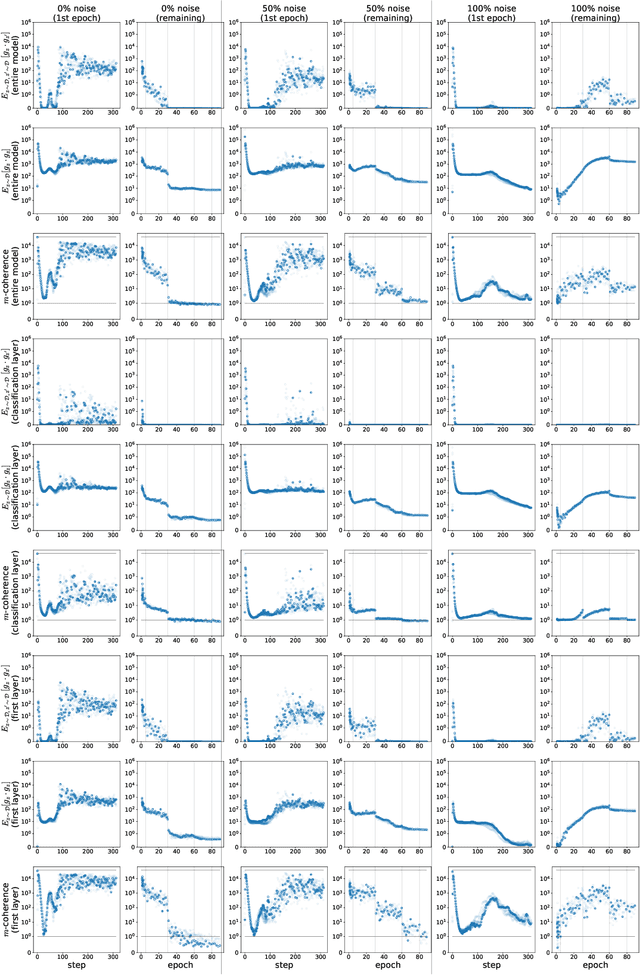
Abstract:We propose a new metric ($m$-coherence) to experimentally study the alignment of per-example gradients during training. Intuitively, given a sample of size $m$, $m$-coherence is the number of examples in the sample that benefit from a small step along the gradient of any one example on average. We show that compared to other commonly used metrics, $m$-coherence is more interpretable, cheaper to compute ($O(m)$ instead of $O(m^2)$) and mathematically cleaner. (We note that $m$-coherence is closely connected to gradient diversity, a quantity previously used in some theoretical bounds.) Using $m$-coherence, we study the evolution of alignment of per-example gradients in ResNet and Inception models on ImageNet and several variants with label noise, particularly from the perspective of the recently proposed Coherent Gradients (CG) theory that provides a simple, unified explanation for memorization and generalization [Chatterjee, ICLR 20]. Although we have several interesting takeaways, our most surprising result concerns memorization. Naively, one might expect that when training with completely random labels, each example is fitted independently, and so $m$-coherence should be close to 1. However, this is not the case: $m$-coherence reaches much higher values during training (100s), indicating that over-parameterized neural networks find common patterns even in scenarios where generalization is not possible. A detailed analysis of this phenomenon provides both a deeper confirmation of CG, but at the same point puts into sharp relief what is missing from the theory in order to provide a complete explanation of generalization in neural networks.
Explaining Memorization and Generalization: A Large-Scale Study with Coherent Gradients
Mar 16, 2020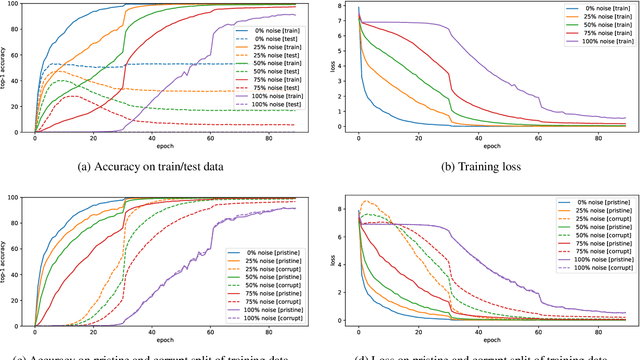
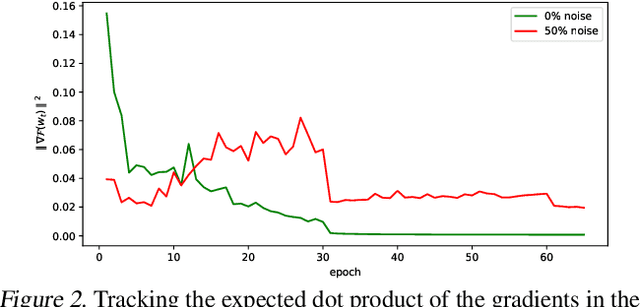
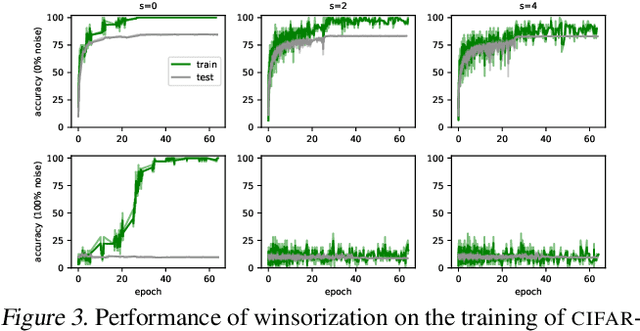

Abstract:Coherent Gradients is a recently proposed hypothesis to explain why over-parameterized neural networks trained with gradient descent generalize well even though they have sufficient capacity to memorize the training set. Inspired by random forests, Coherent Gradients proposes that (Stochastic) Gradient Descent (SGD) finds common patterns amongst examples (if such common patterns exist) since descent directions that are common to many examples add up in the overall gradient, and thus the biggest changes to the network parameters are those that simultaneously help many examples. The original Coherent Gradients paper validated the theory through causal intervention experiments on shallow, fully connected networks on MNIST. In this work, we perform similar intervention experiments on more complex architectures (such as VGG, Inception and ResNet) on more complex datasets (such as CIFAR-10 and ImageNet). Our results are in good agreement with the small scale study in the original paper, thus providing the first validation of coherent gradients in more practically relevant settings. We also confirm in these settings that suppressing incoherent updates by natural modifications to SGD can significantly reduce overfitting--lending credence to the hypothesis that memorization occurs when few examples are responsible for most of the gradient used in the update. Furthermore, we use the coherent gradients theory to explore a new characterization of why some examples are learned earlier than other examples, i.e., "easy" and "hard" examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge