Explaining Memorization and Generalization: A Large-Scale Study with Coherent Gradients

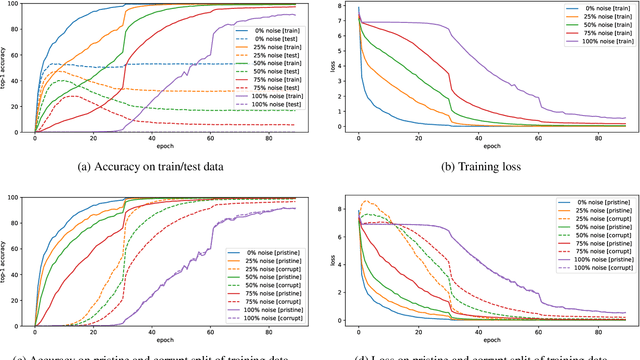
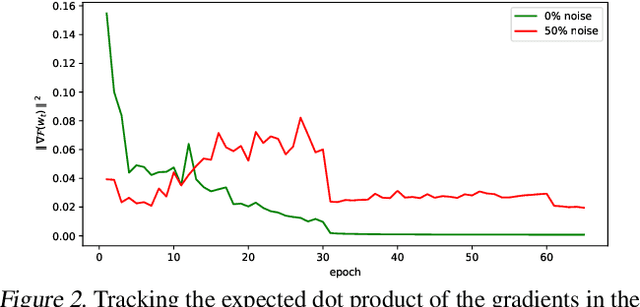
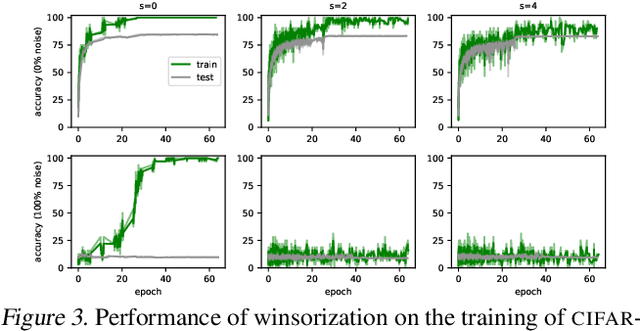
Coherent Gradients is a recently proposed hypothesis to explain why over-parameterized neural networks trained with gradient descent generalize well even though they have sufficient capacity to memorize the training set. Inspired by random forests, Coherent Gradients proposes that (Stochastic) Gradient Descent (SGD) finds common patterns amongst examples (if such common patterns exist) since descent directions that are common to many examples add up in the overall gradient, and thus the biggest changes to the network parameters are those that simultaneously help many examples. The original Coherent Gradients paper validated the theory through causal intervention experiments on shallow, fully connected networks on MNIST. In this work, we perform similar intervention experiments on more complex architectures (such as VGG, Inception and ResNet) on more complex datasets (such as CIFAR-10 and ImageNet). Our results are in good agreement with the small scale study in the original paper, thus providing the first validation of coherent gradients in more practically relevant settings. We also confirm in these settings that suppressing incoherent updates by natural modifications to SGD can significantly reduce overfitting--lending credence to the hypothesis that memorization occurs when few examples are responsible for most of the gradient used in the update. Furthermore, we use the coherent gradients theory to explore a new characterization of why some examples are learned earlier than other examples, i.e., "easy" and "hard" examples.