Making Coherence Out of Nothing At All: Measuring the Evolution of Gradient Alignment
Paper and Code
Aug 03, 2020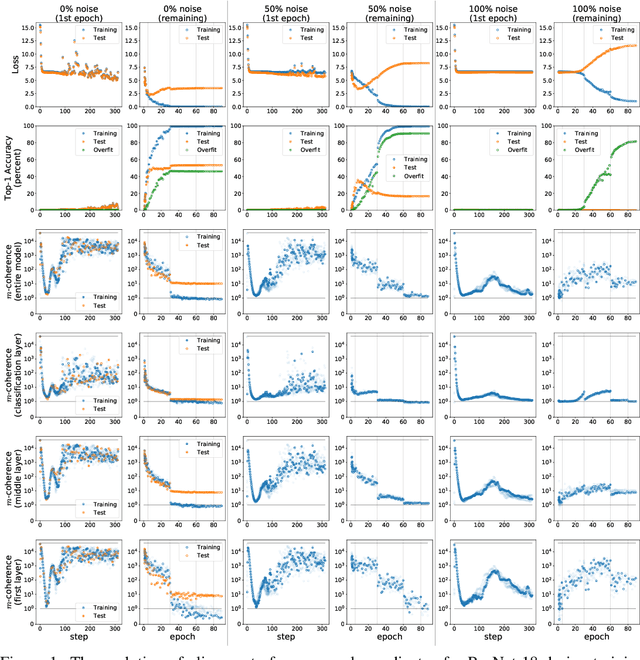
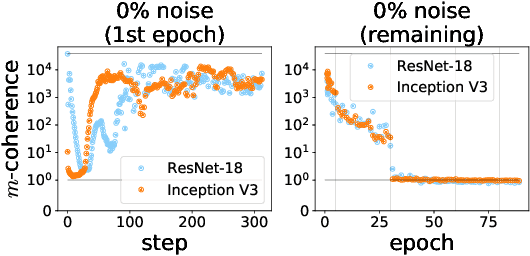
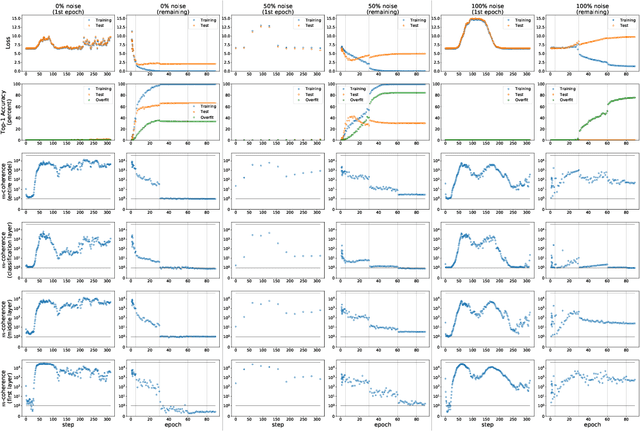
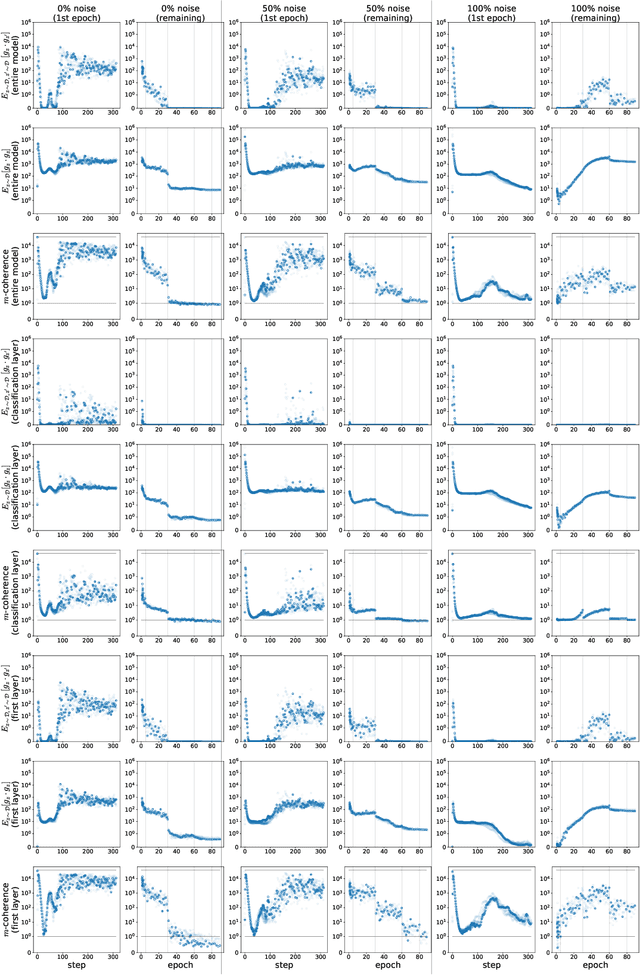
We propose a new metric ($m$-coherence) to experimentally study the alignment of per-example gradients during training. Intuitively, given a sample of size $m$, $m$-coherence is the number of examples in the sample that benefit from a small step along the gradient of any one example on average. We show that compared to other commonly used metrics, $m$-coherence is more interpretable, cheaper to compute ($O(m)$ instead of $O(m^2)$) and mathematically cleaner. (We note that $m$-coherence is closely connected to gradient diversity, a quantity previously used in some theoretical bounds.) Using $m$-coherence, we study the evolution of alignment of per-example gradients in ResNet and Inception models on ImageNet and several variants with label noise, particularly from the perspective of the recently proposed Coherent Gradients (CG) theory that provides a simple, unified explanation for memorization and generalization [Chatterjee, ICLR 20]. Although we have several interesting takeaways, our most surprising result concerns memorization. Naively, one might expect that when training with completely random labels, each example is fitted independently, and so $m$-coherence should be close to 1. However, this is not the case: $m$-coherence reaches much higher values during training (100s), indicating that over-parameterized neural networks find common patterns even in scenarios where generalization is not possible. A detailed analysis of this phenomenon provides both a deeper confirmation of CG, but at the same point puts into sharp relief what is missing from the theory in order to provide a complete explanation of generalization in neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge