BA-BFL: Barycentric Aggregation for Bayesian Federated Learning

In this work, we study the problem of aggregation in the context of Bayesian Federated Learning (BFL). Using an information geometric perspective, we interpret the BFL aggregation step as finding the barycenter of the trained posteriors for a pre-specified divergence metric. We study the barycenter problem for the parametric family of $\alpha$-divergences and, focusing on the standard case of independent and Gaussian distributed parameters, we recover the closed-form solution of the reverse Kullback-Leibler barycenter and develop the analytical form of the squared Wasserstein-2 barycenter. Considering a non-IID setup, where clients possess heterogeneous data, we analyze the performance of the developed algorithms against state-of-the-art (SOTA) Bayesian aggregation methods in terms of accuracy, uncertainty quantification (UQ), model calibration (MC), and fairness. Finally, we extend our analysis to the framework of Hybrid Bayesian Deep Learning (HBDL), where we study how the number of Bayesian layers in the architecture impacts the considered performance metrics. Our experimental results show that the proposed methodology presents comparable performance with the SOTA while offering a geometric interpretation of the aggregation phase.

Alternating Minimization Schemes for Computing Rate-Distortion-Perception Functions with $f$-Divergence Perception Constraints

We study the computation of the rate-distortion-perception function (RDPF) for discrete memoryless sources subject to a single-letter average distortion constraint and a perception constraint that belongs to the family of $f$-divergences. In this setting, the RDPF forms a convex programming problem for which we characterize the optimal parametric solutions. We employ the developed solutions in an alternating minimization scheme, namely Optimal Alternating Minimization (OAM), for which we provide convergence guarantees. Nevertheless, the OAM scheme does not lead to a direct implementation of a generalized Blahut-Arimoto (BA) type of algorithm due to the presence of implicit equations in the structure of the iteration. To overcome this difficulty, we propose two alternative minimization approaches whose applicability depends on the smoothness of the used perception metric: a Newton-based Alternating Minimization (NAM) scheme, relying on Newton's root-finding method for the approximation of the optimal iteration solution, and a Relaxed Alternating Minimization (RAM) scheme, based on a relaxation of the OAM iterates. Both schemes are shown, via the derivation of necessary and sufficient conditions, to guarantee convergence to a globally optimal solution. We also provide sufficient conditions on the distortion and the perception constraints which guarantee that the proposed algorithms converge exponentially fast in the number of iteration steps. We corroborate our theoretical results with numerical simulations and draw connections with existing results.

Goal-Oriented and Semantic Communication in 6G AI-Native Networks: The 6G-GOALS Approach

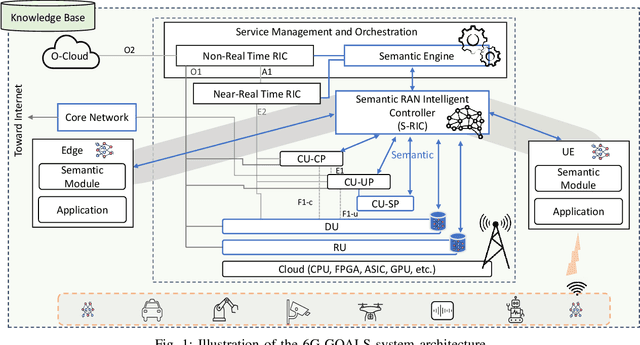
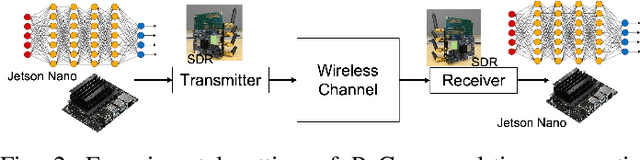
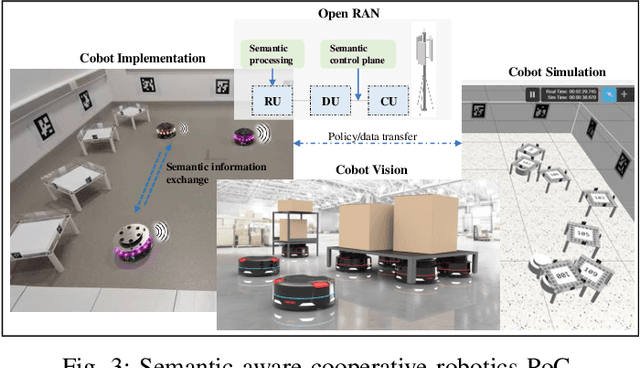
Recent advances in AI technologies have notably expanded device intelligence, fostering federation and cooperation among distributed AI agents. These advancements impose new requirements on future 6G mobile network architectures. To meet these demands, it is essential to transcend classical boundaries and integrate communication, computation, control, and intelligence. This paper presents the 6G-GOALS approach to goal-oriented and semantic communications for AI-Native 6G Networks. The proposed approach incorporates semantic, pragmatic, and goal-oriented communication into AI-native technologies, aiming to facilitate information exchange between intelligent agents in a more relevant, effective, and timely manner, thereby optimizing bandwidth, latency, energy, and electromagnetic field (EMF) radiation. The focus is on distilling data to its most relevant form and terse representation, aligning with the source's intent or the destination's objectives and context, or serving a specific goal. 6G-GOALS builds on three fundamental pillars: i) AI-enhanced semantic data representation, sensing, compression, and communication, ii) foundational AI reasoning and causal semantic data representation, contextual relevance, and value for goal-oriented effectiveness, and iii) sustainability enabled by more efficient wireless services. Finally, we illustrate two proof-of-concepts implementing semantic, goal-oriented, and pragmatic communication principles in near-future use cases. Our study covers the project's vision, methodologies, and potential impact.

On the Computation of the Gaussian Rate-Distortion-Perception Function

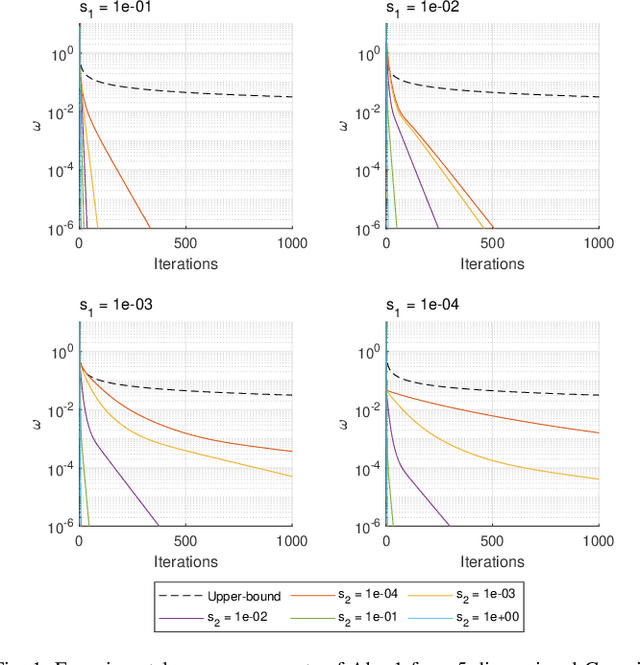
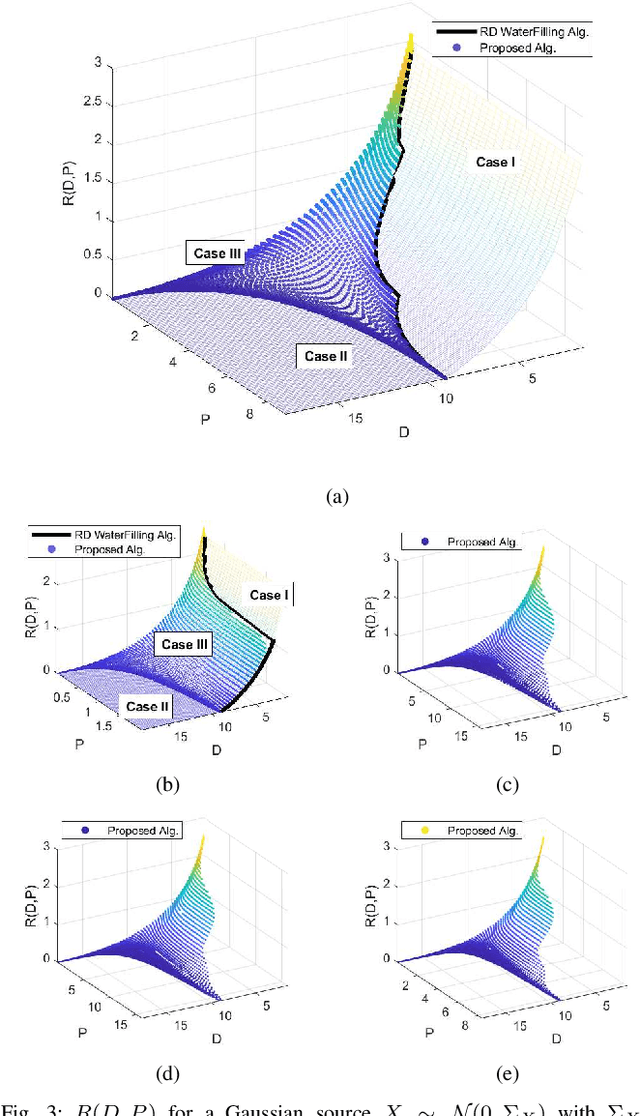
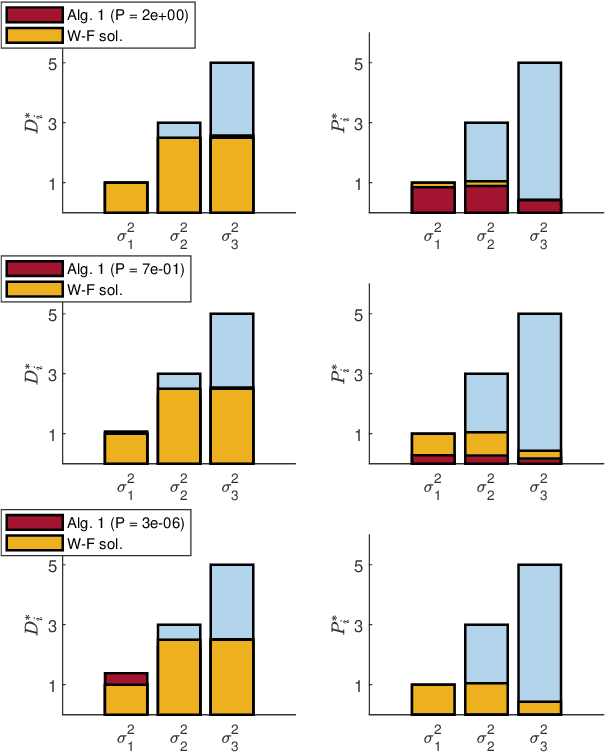
In this paper, we study the computation of the rate-distortion-perception function (RDPF) for a multivariate Gaussian source under mean squared error (MSE) distortion and, respectively, Kullback-Leibler divergence, geometric Jensen-Shannon divergence, squared Hellinger distance, and squared Wasserstein-2 distance perception metrics. To this end, we first characterize the analytical bounds of the scalar Gaussian RDPF for the aforementioned divergence functions, also providing the RDPF-achieving forward "test-channel" realization. Focusing on the multivariate case, we establish that, for tensorizable distortion and perception metrics, the optimal solution resides on the vector space spanned by the eigenvector of the source covariance matrix. Consequently, the multivariate optimization problem can be expressed as a function of the scalar Gaussian RDPFs of the source marginals, constrained by global distortion and perception levels. Leveraging this characterization, we design an alternating minimization scheme based on the block nonlinear Gauss-Seidel method, which optimally solves the problem while identifying the Gaussian RDPF-achieving realization. Furthermore, the associated algorithmic embodiment is provided, as well as the convergence and the rate of convergence characterization. Lastly, for the "perfect realism" regime, the analytical solution for the multivariate Gaussian RDPF is obtained. We corroborate our results with numerical simulations and draw connections to existing results.

Generalized Talagrand Inequality for Sinkhorn Distance using Entropy Power Inequality

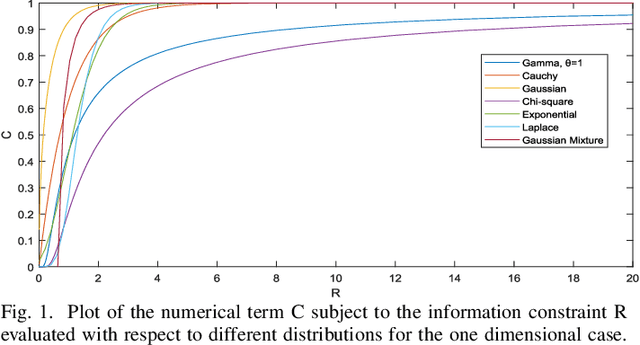
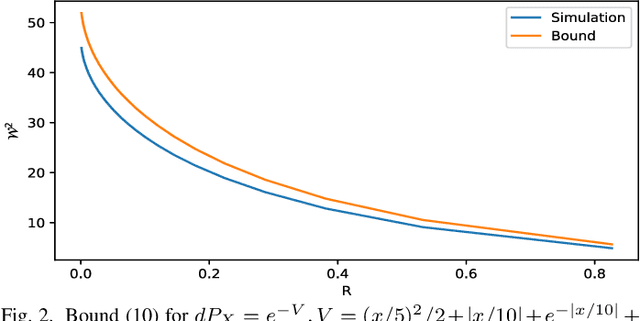
In this paper, we study the connection between entropic optimal transport and entropy power inequality (EPI). First, we prove an HWI-type inequality making use of the infinitesimal displacement convexity of optimal transport map. Second, we derive two Talagrand-type inequalities using the saturation of EPI that corresponds to a numerical term in our expression. We evaluate for a wide variety of distributions this term whereas for Gaussian and i.i.d. Cauchy distributions this term is found in explicit form. We show that our results extend previous results of Gaussian Talagrand inequality for Sinkhorn distance to the strongly log-concave case.