Generalized Talagrand Inequality for Sinkhorn Distance using Entropy Power Inequality
Paper and Code
Sep 17, 2021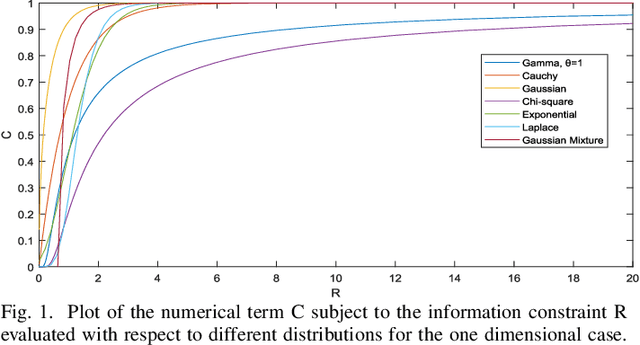
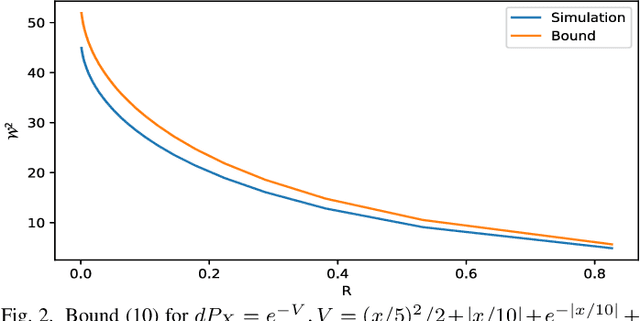
In this paper, we study the connection between entropic optimal transport and entropy power inequality (EPI). First, we prove an HWI-type inequality making use of the infinitesimal displacement convexity of optimal transport map. Second, we derive two Talagrand-type inequalities using the saturation of EPI that corresponds to a numerical term in our expression. We evaluate for a wide variety of distributions this term whereas for Gaussian and i.i.d. Cauchy distributions this term is found in explicit form. We show that our results extend previous results of Gaussian Talagrand inequality for Sinkhorn distance to the strongly log-concave case.
* The paper has been accepted to Information Theory Workshop 2021
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge