SE(3)-MeanFlow: Few-Step Protein Backbone Generation on Lie Groups

Generative modeling of protein backbones promises the de novo design of proteins with prescribed structural and functional properties. Existing diffusion and flow-matching models produce high-quality backbones on SE(3)^N, but inference requires numerically integrating an ODE over hundreds of network evaluations, each involving a Lie group exponential map - a bottleneck for high-throughput design campaigns. We introduce SE(3)-MeanFlow, a few-step generative framework that extends MeanFlow from Euclidean space to the Lie group geometry of protein frames. Working natively in the Lie algebra so(3) and in R^3, we derive closed-form average-velocity identities for rotations and translations, giving simulation-free training targets. We further introduce an SE(3) alpha-Flow objective that removes the Jacobian-vector product from the rotation branch and serves as a warm-up stage, after which training switches to a small-t stabilized MeanFlow loss that is used for the remainder of pretraining and for rectification-based post-training. In protein backbone generation, SE(3)-MeanFlow matches or exceeds flow-matching baselines that use several times more sampling steps, and its advantage widens in the few-step regime, where rectification lets it lead at every matched budget - at a modest cost in diversity.

The Geometry of Memorization: Finite-Time Spectral Sensitivity as a Diagnostic for Flow Matching Models

Continuous-time generative frameworks construct probability paths between base and target domains by optimizing time-dependent velocity fields. While theoretical targets favor straight trajectories, empirical networks develop complex path deformations. This paper presents the Finite-Time Spectral Sensitivity (FTSS) g(t), a gradient-free, forward-pass metric that exposes flow geometry by tracking the root-mean-square singular value of the state-transition matrix. Serving as a continuous proxy for stable rank, g(t) reveals a distinct geometric pathology under data scarcity: while generalizing models maintain stable effective dimensions, overfitting causes a spectral collapse. We leverage this structural phenomenon to develop an internal geometric audit based on g(t). Our framework detects generative memorization using purely internal trajectory dynamics, removing the need for external membership queries or baseline data comparison.

Information-Theoretic Equivalence of Entropic Multi-Marginal Optimal Transport: A Theory for Multi-Agent Communication

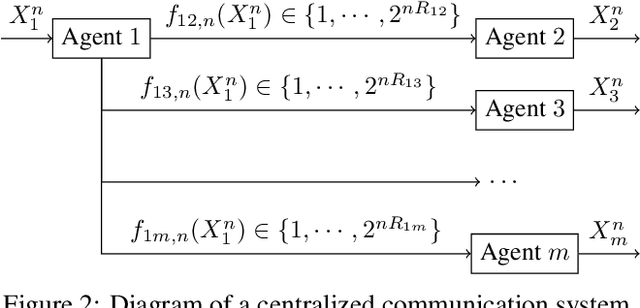
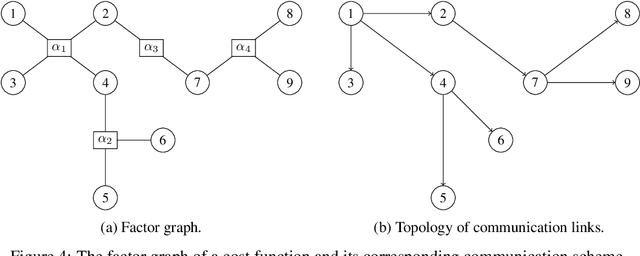
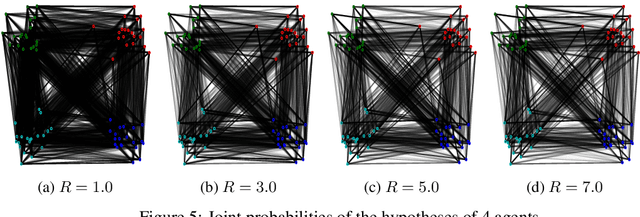
In this paper, we propose our information-theoretic equivalence of entropic multi-marginal optimal transport (MOT). This equivalence can be easily reduced to the case of entropic optimal transport (OT). Because OT is widely used to compare differences between knowledge or beliefs, we apply this result to the communication between agents with different beliefs. Our results formally prove the statement that entropic OT is information-theoretically optimal given by Wang et al. [2020] and generalize it to the multi-agent case. We believe that our work can shed light on OT theory in future multi-agent teaming systems.

Generalized Talagrand Inequality for Sinkhorn Distance using Entropy Power Inequality

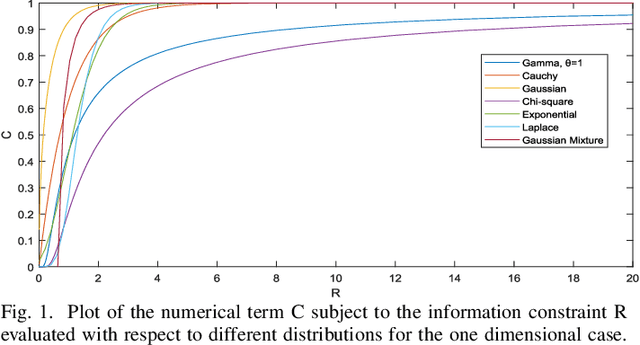
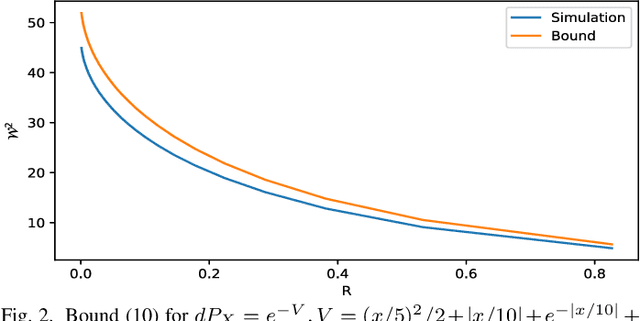
In this paper, we study the connection between entropic optimal transport and entropy power inequality (EPI). First, we prove an HWI-type inequality making use of the infinitesimal displacement convexity of optimal transport map. Second, we derive two Talagrand-type inequalities using the saturation of EPI that corresponds to a numerical term in our expression. We evaluate for a wide variety of distributions this term whereas for Gaussian and i.i.d. Cauchy distributions this term is found in explicit form. We show that our results extend previous results of Gaussian Talagrand inequality for Sinkhorn distance to the strongly log-concave case.