Peter Davies
CyRes -- Avoiding Catastrophic Failure in Connected and Autonomous Vehicles (Extended Abstract)
Jul 03, 2020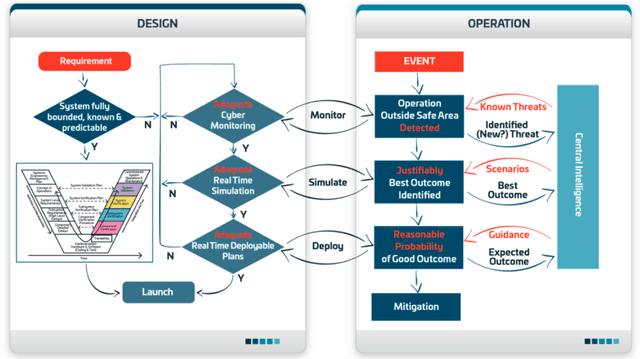

Abstract:Existing approaches to cyber security and regulation in the automotive sector cannot achieve the quality of outcome necessary to ensure the safe mass deployment of advanced vehicle technologies and smart mobility systems. Without sustainable resilience hard-fought public trust will evaporate, derailing emerging global initiatives to improve the efficiency, safety and environmental impact of future transport. This paper introduces an operational cyber resilience methodology, CyRes, that is suitable for standardisation. The CyRes methodology itself is capable of being tested in court or by publicly appointed regulators. It is designed so that operators understand what evidence should be produced by it and are able to measure the quality of that evidence. The evidence produced is capable of being tested in court or by publicly appointed regulators. Thus, the real-world system to which the CyRes methodology has been applied is capable of operating at all times and in all places with a legally and socially acceptable value of negative consequence.
Distributed Mean Estimation with Optimal Error Bounds
Feb 24, 2020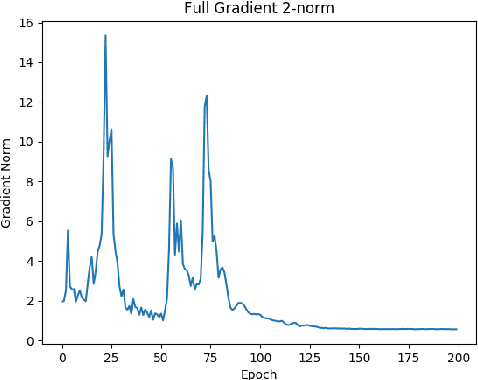
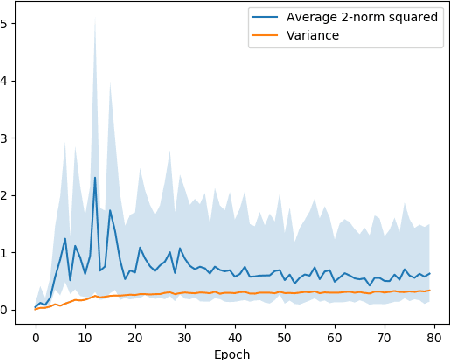
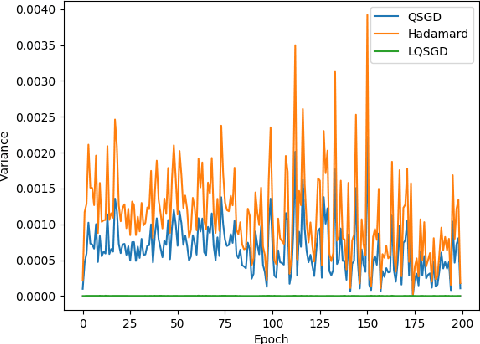
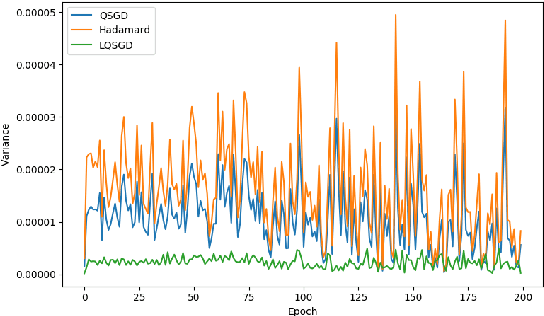
Abstract:Motivated by applications to distributed optimization and machine learning, we consider the distributed mean estimation problem, in which $n$ nodes are each assigned a multi-dimensional input vector, and must cooperate to estimate the mean of the input vectors, while minimizing communication. In this paper, we provide the first tight bounds for this problem, in terms of the trade-off between the amount of communication between nodes and the variance of the node estimates relative to the true value of the mean.
SPONGE: A generalized eigenproblem for clustering signed networks
May 19, 2019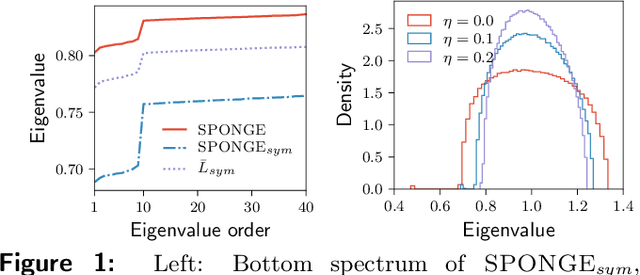

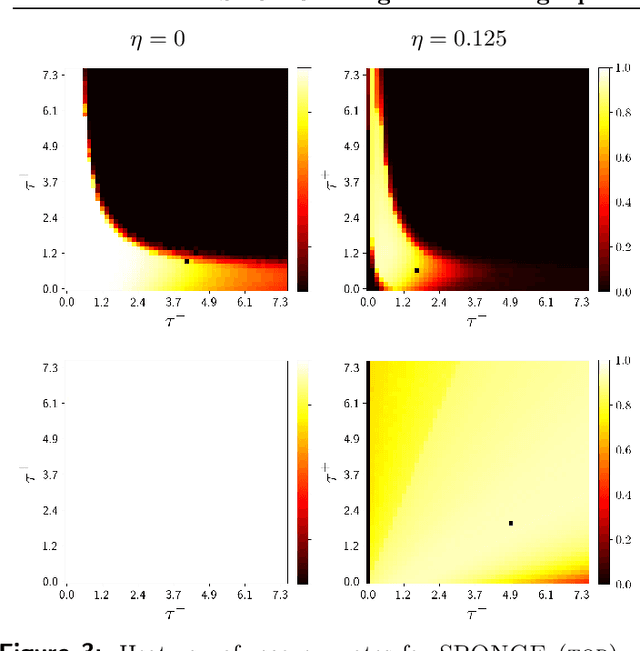
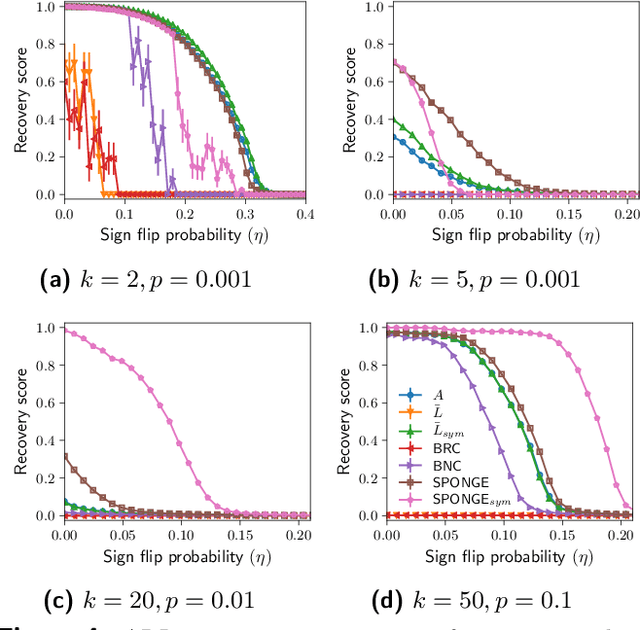
Abstract:We introduce a principled and theoretically sound spectral method for $k$-way clustering in signed graphs, where the affinity measure between nodes takes either positive or negative values. Our approach is motivated by social balance theory, where the task of clustering aims to decompose the network into disjoint groups, such that individuals within the same group are connected by as many positive edges as possible, while individuals from different groups are connected by as many negative edges as possible. Our algorithm relies on a generalized eigenproblem formulation inspired by recent work on constrained clustering. We provide theoretical guarantees for our approach in the setting of a signed stochastic block model, by leveraging tools from matrix perturbation theory and random matrix theory. An extensive set of numerical experiments on both synthetic and real data shows that our approach compares favorably with state-of-the-art methods for signed clustering, especially for large number of clusters and sparse measurement graphs.
* 33 pages, 18 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge