SPONGE: A generalized eigenproblem for clustering signed networks
Paper and Code
May 19, 2019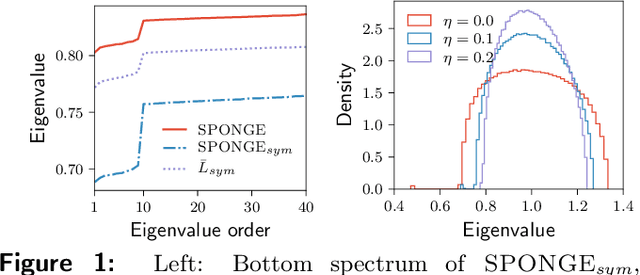

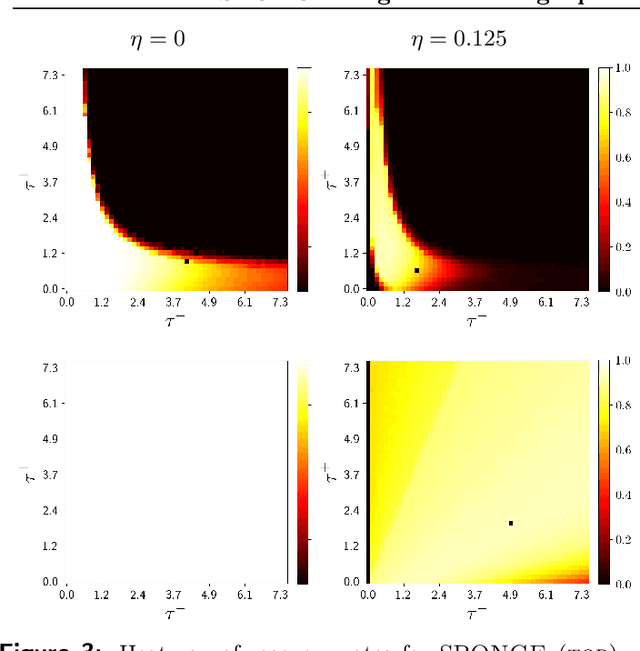
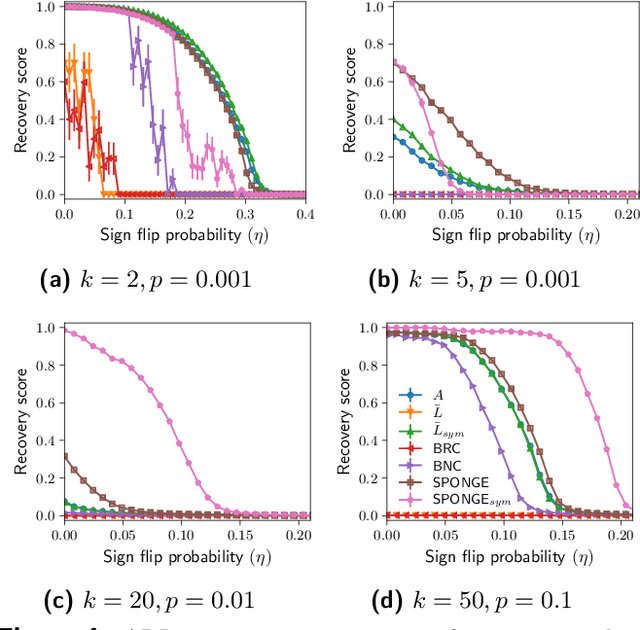
We introduce a principled and theoretically sound spectral method for $k$-way clustering in signed graphs, where the affinity measure between nodes takes either positive or negative values. Our approach is motivated by social balance theory, where the task of clustering aims to decompose the network into disjoint groups, such that individuals within the same group are connected by as many positive edges as possible, while individuals from different groups are connected by as many negative edges as possible. Our algorithm relies on a generalized eigenproblem formulation inspired by recent work on constrained clustering. We provide theoretical guarantees for our approach in the setting of a signed stochastic block model, by leveraging tools from matrix perturbation theory and random matrix theory. An extensive set of numerical experiments on both synthetic and real data shows that our approach compares favorably with state-of-the-art methods for signed clustering, especially for large number of clusters and sparse measurement graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge