Distributed Mean Estimation with Optimal Error Bounds
Paper and Code
Feb 24, 2020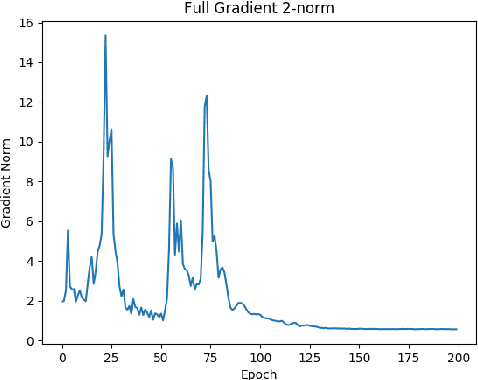
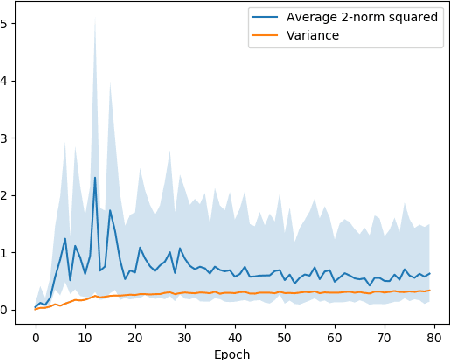
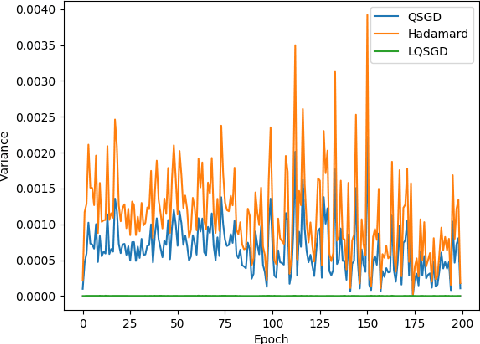
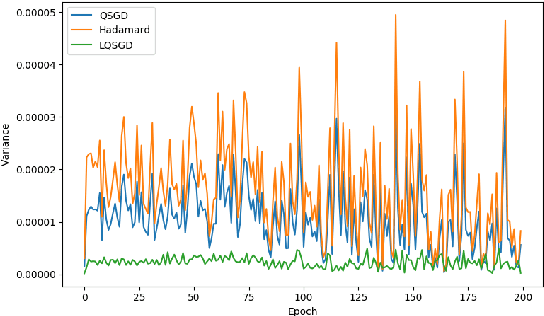
Motivated by applications to distributed optimization and machine learning, we consider the distributed mean estimation problem, in which $n$ nodes are each assigned a multi-dimensional input vector, and must cooperate to estimate the mean of the input vectors, while minimizing communication. In this paper, we provide the first tight bounds for this problem, in terms of the trade-off between the amount of communication between nodes and the variance of the node estimates relative to the true value of the mean.
* 19 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge