Neural ODEs as Feedback Policies for Nonlinear Optimal Control

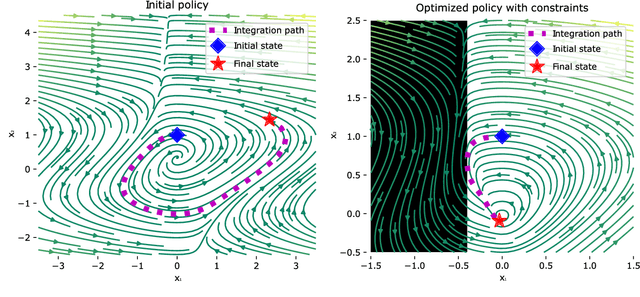
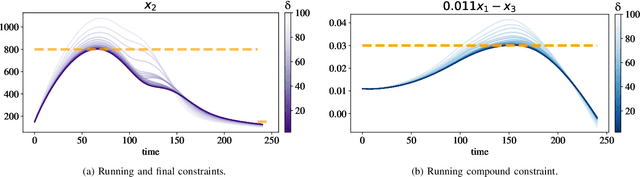
Neural ordinary differential equations (Neural ODEs) model continuous time dynamics as differential equations parametrized with neural networks. Thanks to their modeling flexibility, they have been adopted for multiple tasks where the continuous time nature of the process is specially relevant, as in system identification and time series analysis. When applied in a control setting, it is possible to adapt their use to approximate optimal nonlinear feedback policies. This formulation follows the same approach as policy gradients in reinforcement learning, covering the case where the environment consists of known deterministic dynamics given by a system of differential equations. The white box nature of the model specification allows the direct calculation of policy gradients through sensitivity analysis, avoiding the inexact and inefficient gradient estimation through sampling. In this work we propose the use of a neural control policy posed as a Neural ODE to solve general nonlinear optimal control problems while satisfying both state and control constraints, which are crucial for real world scenarios. Since the state feedback policy partially modifies the model dynamics, the whole space phase of the system is reshaped upon the optimization. This approach is a sensible approximation to the historically intractable closed loop solution of nonlinear control problems that efficiently exploits the availability of a dynamical system model.

Safe Real-Time Optimization using Multi-Fidelity Gaussian Processes

This paper proposes a new class of real-time optimization schemes to overcome system-model mismatch of uncertain processes. This work's novelty lies in integrating derivative-free optimization schemes and multi-fidelity Gaussian processes within a Bayesian optimization framework. The proposed scheme uses two Gaussian processes for the stochastic system, one emulates the (known) process model, and another, the true system through measurements. In this way, low fidelity samples can be obtained via a model, while high fidelity samples are obtained through measurements of the system. This framework captures the system's behavior in a non-parametric fashion while driving exploration through acquisition functions. The benefit of using a Gaussian process to represent the system is the ability to perform uncertainty quantification in real-time and allow for chance constraints to be satisfied with high confidence. This results in a practical approach that is illustrated in numerical case studies, including a semi-batch photobioreactor optimization problem.

Safe Chance Constrained Reinforcement Learning for Batch Process Control

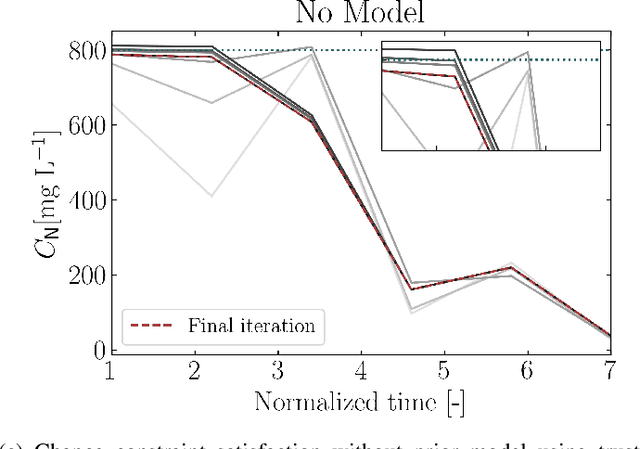
Reinforcement Learning (RL) controllers have generated excitement within the control community. The primary advantage of RL controllers relative to existing methods is their ability to optimize uncertain systems independently of explicit assumption of process uncertainty. Recent focus on engineering applications has been directed towards the development of safe RL controllers. Previous works have proposed approaches to account for constraint satisfaction through constraint tightening from the domain of stochastic model predictive control. Here, we extend these approaches to account for plant-model mismatch. Specifically, we propose a data-driven approach that utilizes Gaussian processes for the offline simulation model and use the associated posterior uncertainty prediction to account for joint chance constraints and plant-model mismatch. The method is benchmarked against nonlinear model predictive control via case studies. The results demonstrate the ability of the methodology to account for process uncertainty, enabling satisfaction of joint chance constraints even in the presence of plant-model mismatch.

Constrained Model-Free Reinforcement Learning for Process Optimization

Reinforcement learning (RL) is a control approach that can handle nonlinear stochastic optimal control problems. However, despite the promise exhibited, RL has yet to see marked translation to industrial practice primarily due to its inability to satisfy state constraints. In this work we aim to address this challenge. We propose an 'oracle'-assisted constrained Q-learning algorithm that guarantees the satisfaction of joint chance constraints with a high probability, which is crucial for safety critical tasks. To achieve this, constraint tightening (backoffs) are introduced and adjusted using Broyden's method, hence making them self-tuned. This results in a general methodology that can be imbued into approximate dynamic programming-based algorithms to ensure constraint satisfaction with high probability. Finally, we present case studies that analyze the performance of the proposed approach and compare this algorithm with model predictive control (MPC). The favorable performance of this algorithm signifies a step toward the incorporation of RL into real world optimization and control of engineering systems, where constraints are essential in ensuring safety.

Modifier Adaptation Meets Bayesian Optimization and Derivative-Free Optimization

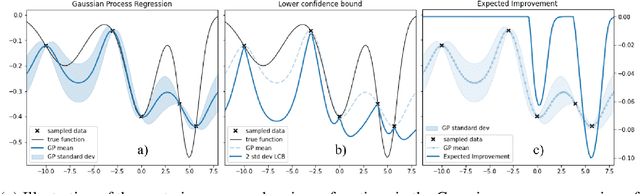
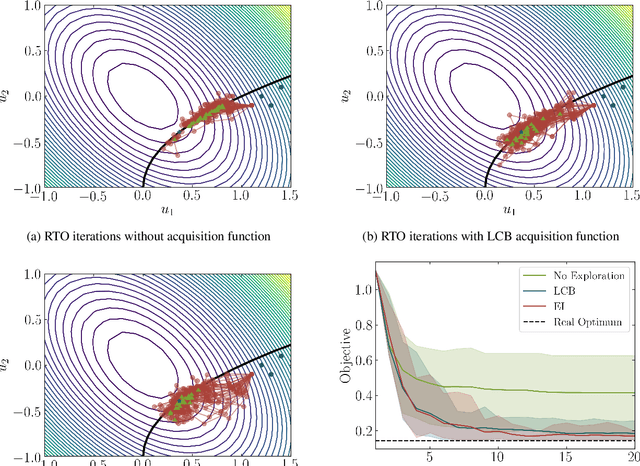
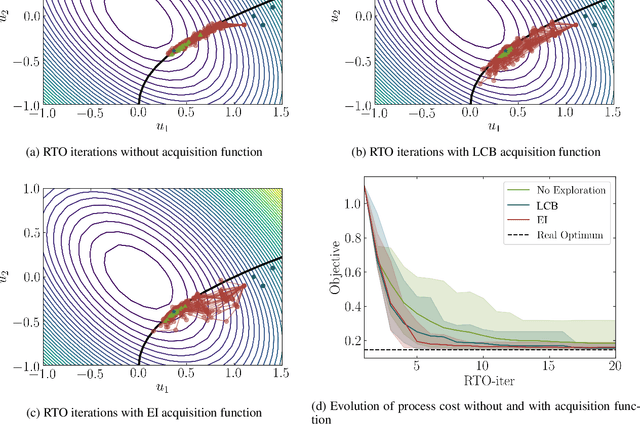
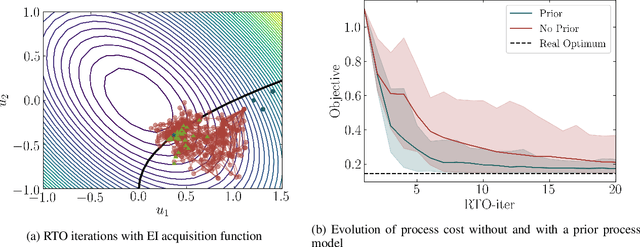
This paper investigates a new class of modifier-adaptation schemes to overcome plant-model mismatch in real-time optimization of uncertain processes. The main contribution lies in the integration of concepts from the areas of Bayesian optimization and derivative-free optimization. The proposed schemes embed a physical model and rely on trust-region ideas to minimize risk during the exploration, while employing Gaussian process regression to capture the plant-model mismatch in a non-parametric way and drive the exploration by means of acquisition functions. The benefits of using an acquisition function, knowing the process noise level, or specifying a nominal process model are illustrated on numerical case studies, including a semi-batch photobioreactor optimization problem.

Chance Constrained Policy Optimization for Process Control and Optimization

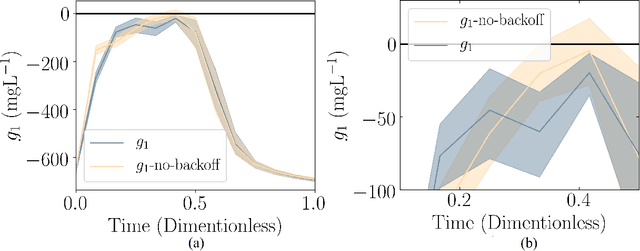
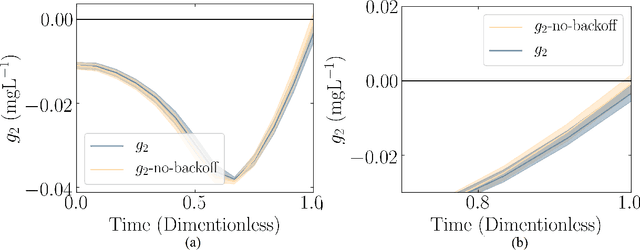
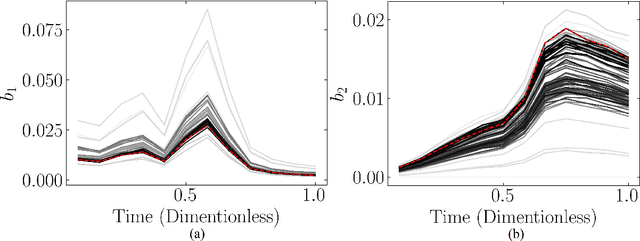
Chemical process optimization and control are affected by 1) plant-model mismatch, 2) process disturbances, and 3) constraints for safe operation. Reinforcement learning by policy optimization would be a natural way to solve this due to its ability to address stochasticity, plant-model mismatch, and directly account for the effect of future uncertainty and its feedback in a proper closed-loop manner; all without the need of an inner optimization loop. One of the main reasons why reinforcement learning has not been considered for industrial processes (or almost any engineering application) is that it lacks a framework to deal with safety critical constraints. Present algorithms for policy optimization use difficult-to-tune penalty parameters, fail to reliably satisfy state constraints or present guarantees only in expectation. We propose a chance constrained policy optimization (CCPO) algorithm which guarantees the satisfaction of joint chance constraints with a high probability - which is crucial for safety critical tasks. This is achieved by the introduction of constraint tightening (backoffs), which are computed simultaneously with the feedback policy. Backoffs are adjusted with Bayesian optimization using the empirical cumulative distribution function of the probabilistic constraints, and are therefore self-tuned. This results in a general methodology that can be imbued into present policy optimization algorithms to enable them to satisfy joint chance constraints with high probability. We present case studies that analyze the performance of the proposed approach.

Constrained Reinforcement Learning for Dynamic Optimization under Uncertainty

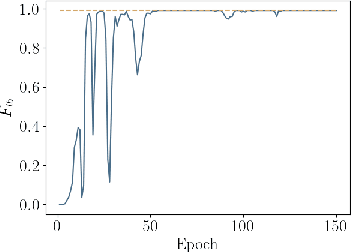
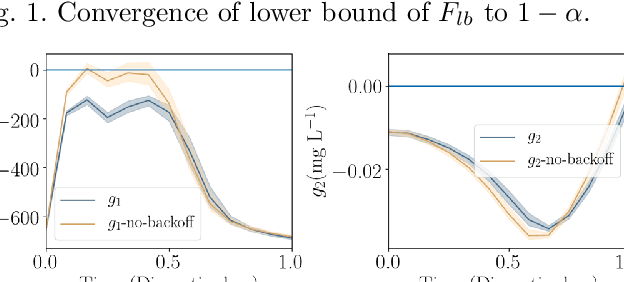
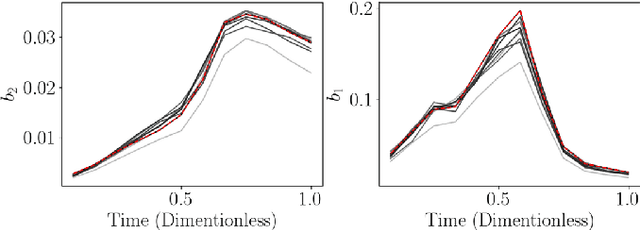
Dynamic real-time optimization (DRTO) is a challenging task due to the fact that optimal operating conditions must be computed in real time. The main bottleneck in the industrial application of DRTO is the presence of uncertainty. Many stochastic systems present the following obstacles: 1) plant-model mismatch, 2) process disturbances, 3) risks in violation of process constraints. To accommodate these difficulties, we present a constrained reinforcement learning (RL) based approach. RL naturally handles the process uncertainty by computing an optimal feedback policy. However, no state constraints can be introduced intuitively. To address this problem, we present a chance-constrained RL methodology. We use chance constraints to guarantee the probabilistic satisfaction of process constraints, which is accomplished by introducing backoffs, such that the optimal policy and backoffs are computed simultaneously. Backoffs are adjusted using the empirical cumulative distribution function to guarantee the satisfaction of a joint chance constraint. The advantage and performance of this strategy are illustrated through a stochastic dynamic bioprocess optimization problem, to produce sustainable high-value bioproducts.