Machine learning for industrial sensing and control: A survey and practical perspective

With the rise of deep learning, there has been renewed interest within the process industries to utilize data on large-scale nonlinear sensing and control problems. We identify key statistical and machine learning techniques that have seen practical success in the process industries. To do so, we start with hybrid modeling to provide a methodological framework underlying core application areas: soft sensing, process optimization, and control. Soft sensing contains a wealth of industrial applications of statistical and machine learning methods. We quantitatively identify research trends, allowing insight into the most successful techniques in practice. We consider two distinct flavors for data-driven optimization and control: hybrid modeling in conjunction with mathematical programming techniques and reinforcement learning. Throughout these application areas, we discuss their respective industrial requirements and challenges. A common challenge is the interpretability and efficiency of purely data-driven methods. This suggests a need to carefully balance deep learning techniques with domain knowledge. As a result, we highlight ways prior knowledge may be integrated into industrial machine learning applications. The treatment of methods, problems, and applications presented here is poised to inform and inspire practitioners and researchers to develop impactful data-driven sensing, optimization, and control solutions in the process industries.

Modern Machine Learning Tools for Monitoring and Control of Industrial Processes: A Survey

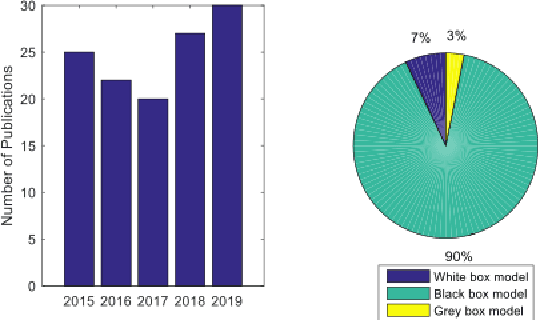
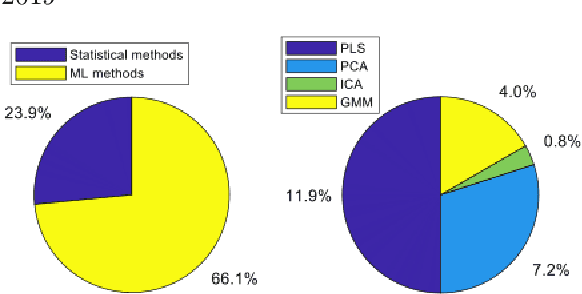
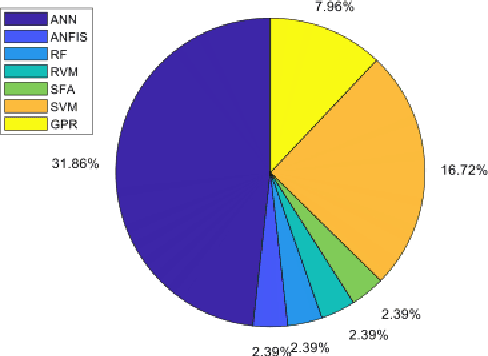
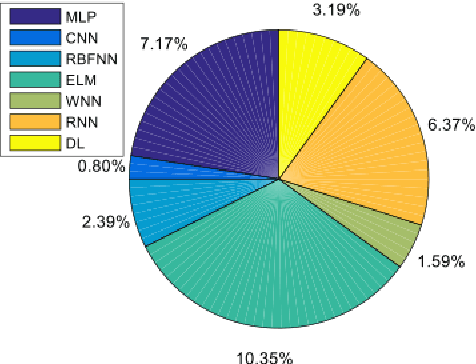
Over the last ten years, we have seen a significant increase in industrial data, tremendous improvement in computational power, and major theoretical advances in machine learning. This opens up an opportunity to use modern machine learning tools on large-scale nonlinear monitoring and control problems. This article provides a survey of recent results with applications in the process industry.

Safe Real-Time Optimization using Multi-Fidelity Gaussian Processes

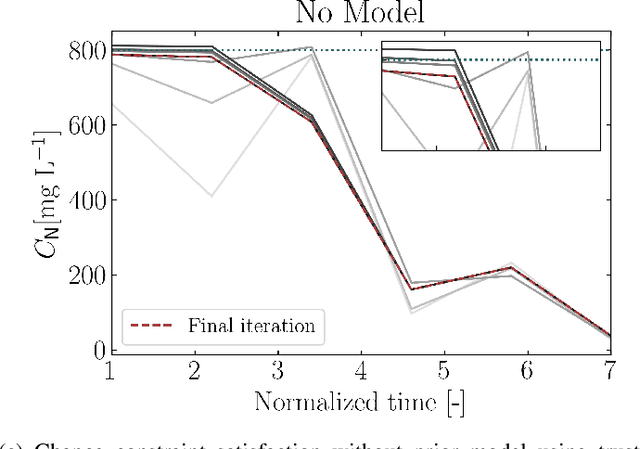
This paper proposes a new class of real-time optimization schemes to overcome system-model mismatch of uncertain processes. This work's novelty lies in integrating derivative-free optimization schemes and multi-fidelity Gaussian processes within a Bayesian optimization framework. The proposed scheme uses two Gaussian processes for the stochastic system, one emulates the (known) process model, and another, the true system through measurements. In this way, low fidelity samples can be obtained via a model, while high fidelity samples are obtained through measurements of the system. This framework captures the system's behavior in a non-parametric fashion while driving exploration through acquisition functions. The benefit of using a Gaussian process to represent the system is the ability to perform uncertainty quantification in real-time and allow for chance constraints to be satisfied with high confidence. This results in a practical approach that is illustrated in numerical case studies, including a semi-batch photobioreactor optimization problem.

Modifier Adaptation Meets Bayesian Optimization and Derivative-Free Optimization

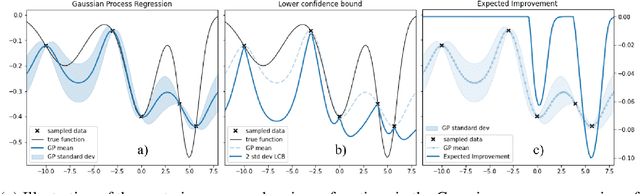
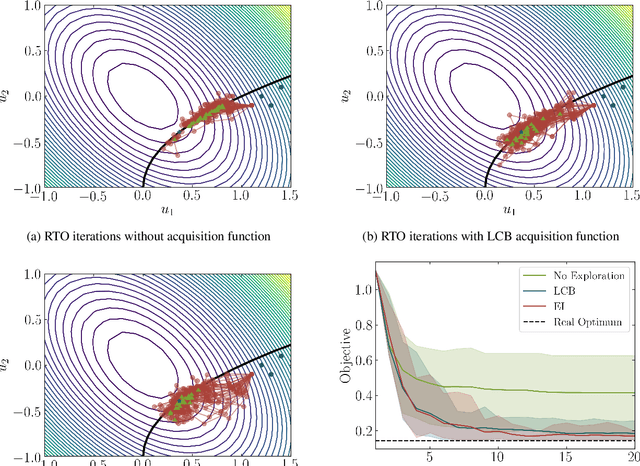
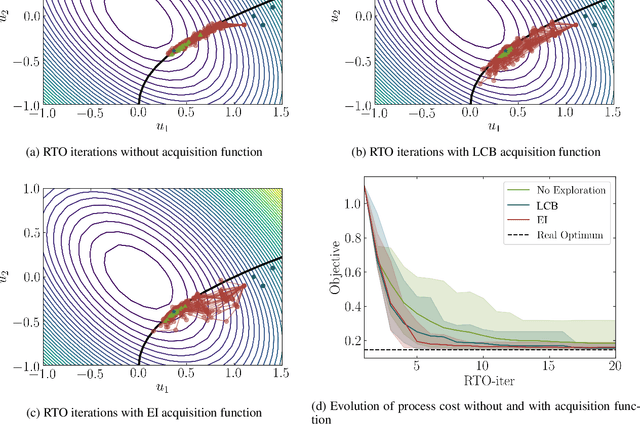
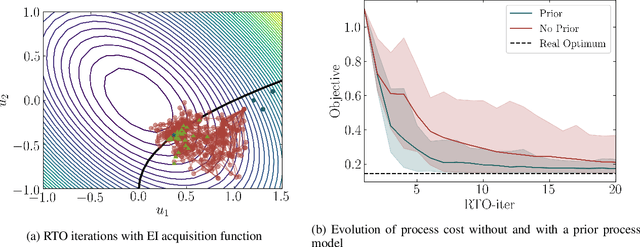
This paper investigates a new class of modifier-adaptation schemes to overcome plant-model mismatch in real-time optimization of uncertain processes. The main contribution lies in the integration of concepts from the areas of Bayesian optimization and derivative-free optimization. The proposed schemes embed a physical model and rely on trust-region ideas to minimize risk during the exploration, while employing Gaussian process regression to capture the plant-model mismatch in a non-parametric way and drive the exploration by means of acquisition functions. The benefits of using an acquisition function, knowing the process noise level, or specifying a nominal process model are illustrated on numerical case studies, including a semi-batch photobioreactor optimization problem.

Bayesian Optimization with Dimension Scheduling: Application to Biological Systems

Bayesian Optimization (BO) is a data-efficient method for global black-box optimization of an expensive-to-evaluate fitness function. BO typically assumes that computation cost of BO is cheap, but experiments are time consuming or costly. In practice, this allows us to optimize ten or fewer critical parameters in up to 1,000 experiments. But experiments may be less expensive than BO methods assume: In some simulation models, we may be able to conduct multiple thousands of experiments in a few hours, and the computational burden of BO is no longer negligible compared to experimentation time. To address this challenge we introduce a new Dimension Scheduling Algorithm (DSA), which reduces the computational burden of BO for many experiments. The key idea is that DSA optimizes the fitness function only along a small set of dimensions at each iteration. This DSA strategy (1) reduces the necessary computation time, (2) finds good solutions faster than the traditional BO method, and (3) can be parallelized straightforwardly. We evaluate the DSA in the context of optimizing parameters of dynamic models of microalgae metabolism and show faster convergence than traditional BO.