An Analysis of Multi-Agent Reinforcement Learning for Decentralized Inventory Control Systems

Most solutions to the inventory management problem assume a centralization of information that is incompatible with organisational constraints in real supply chain networks. The inventory management problem is a well-known planning problem in operations research, concerned with finding the optimal re-order policy for nodes in a supply chain. While many centralized solutions to the problem exist, they are not applicable to real-world supply chains made up of independent entities. The problem can however be naturally decomposed into sub-problems, each associated with an independent entity, turning it into a multi-agent system. Therefore, a decentralized data-driven solution to inventory management problems using multi-agent reinforcement learning is proposed where each entity is controlled by an agent. Three multi-agent variations of the proximal policy optimization algorithm are investigated through simulations of different supply chain networks and levels of uncertainty. The centralized training decentralized execution framework is deployed, which relies on offline centralization during simulation-based policy identification, but enables decentralization when the policies are deployed online to the real system. Results show that using multi-agent proximal policy optimization with a centralized critic leads to performance very close to that of a centralized data-driven solution and outperforms a distributed model-based solution in most cases while respecting the information constraints of the system.

Neural ODEs as Feedback Policies for Nonlinear Optimal Control

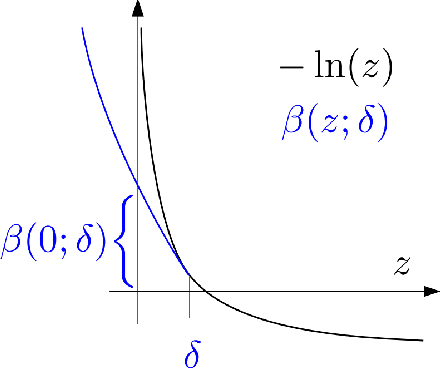
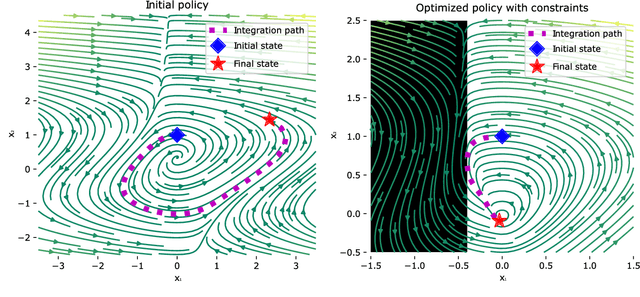
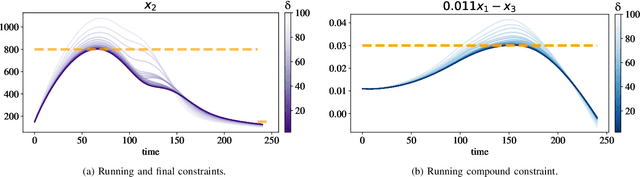
Neural ordinary differential equations (Neural ODEs) model continuous time dynamics as differential equations parametrized with neural networks. Thanks to their modeling flexibility, they have been adopted for multiple tasks where the continuous time nature of the process is specially relevant, as in system identification and time series analysis. When applied in a control setting, it is possible to adapt their use to approximate optimal nonlinear feedback policies. This formulation follows the same approach as policy gradients in reinforcement learning, covering the case where the environment consists of known deterministic dynamics given by a system of differential equations. The white box nature of the model specification allows the direct calculation of policy gradients through sensitivity analysis, avoiding the inexact and inefficient gradient estimation through sampling. In this work we propose the use of a neural control policy posed as a Neural ODE to solve general nonlinear optimal control problems while satisfying both state and control constraints, which are crucial for real world scenarios. Since the state feedback policy partially modifies the model dynamics, the whole space phase of the system is reshaped upon the optimization. This approach is a sensible approximation to the historically intractable closed loop solution of nonlinear control problems that efficiently exploits the availability of a dynamical system model.

Safe Real-Time Optimization using Multi-Fidelity Gaussian Processes

This paper proposes a new class of real-time optimization schemes to overcome system-model mismatch of uncertain processes. This work's novelty lies in integrating derivative-free optimization schemes and multi-fidelity Gaussian processes within a Bayesian optimization framework. The proposed scheme uses two Gaussian processes for the stochastic system, one emulates the (known) process model, and another, the true system through measurements. In this way, low fidelity samples can be obtained via a model, while high fidelity samples are obtained through measurements of the system. This framework captures the system's behavior in a non-parametric fashion while driving exploration through acquisition functions. The benefit of using a Gaussian process to represent the system is the ability to perform uncertainty quantification in real-time and allow for chance constraints to be satisfied with high confidence. This results in a practical approach that is illustrated in numerical case studies, including a semi-batch photobioreactor optimization problem.

Modifier Adaptation Meets Bayesian Optimization and Derivative-Free Optimization

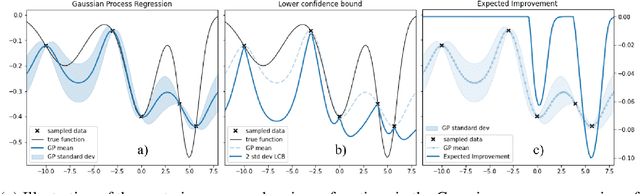
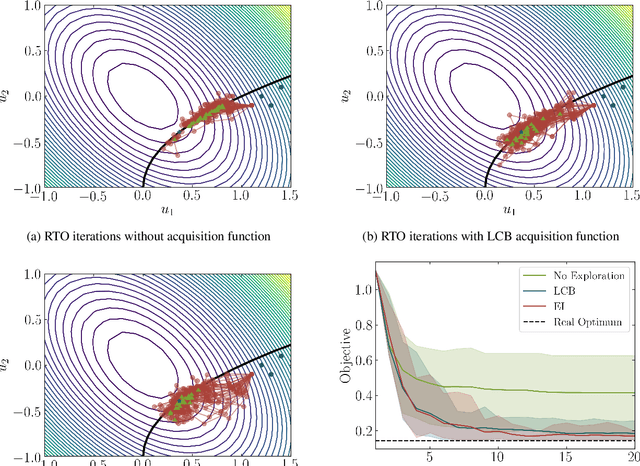
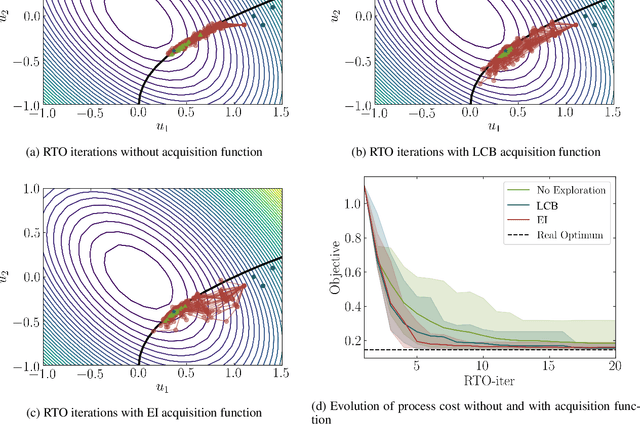
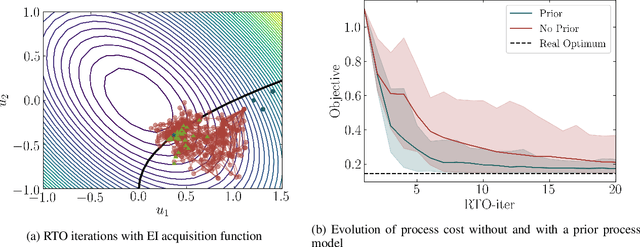
This paper investigates a new class of modifier-adaptation schemes to overcome plant-model mismatch in real-time optimization of uncertain processes. The main contribution lies in the integration of concepts from the areas of Bayesian optimization and derivative-free optimization. The proposed schemes embed a physical model and rely on trust-region ideas to minimize risk during the exploration, while employing Gaussian process regression to capture the plant-model mismatch in a non-parametric way and drive the exploration by means of acquisition functions. The benefits of using an acquisition function, knowing the process noise level, or specifying a nominal process model are illustrated on numerical case studies, including a semi-batch photobioreactor optimization problem.

Chance Constrained Policy Optimization for Process Control and Optimization

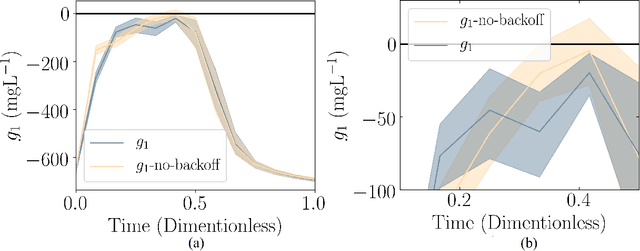
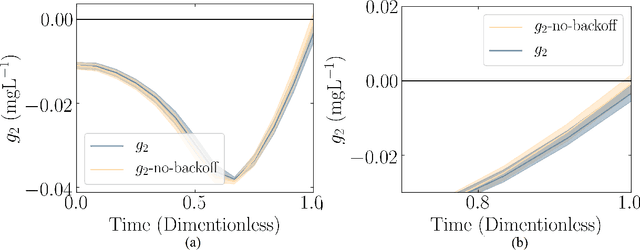
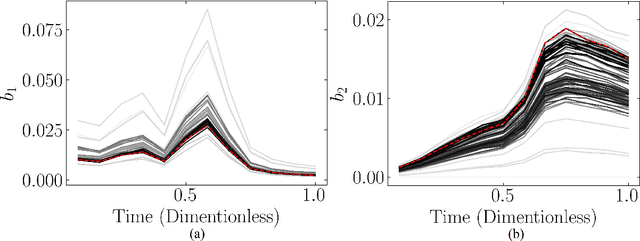
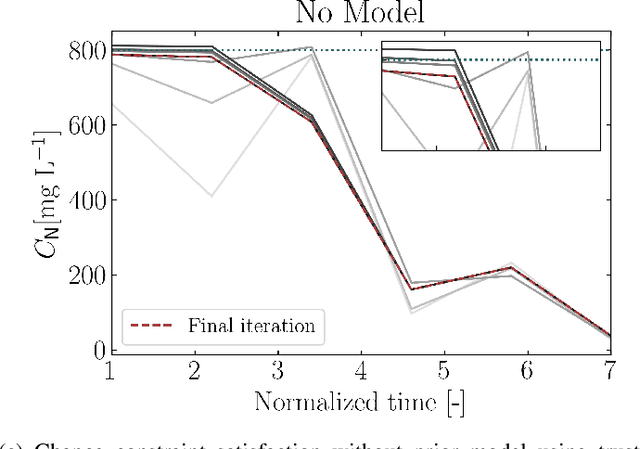
Chemical process optimization and control are affected by 1) plant-model mismatch, 2) process disturbances, and 3) constraints for safe operation. Reinforcement learning by policy optimization would be a natural way to solve this due to its ability to address stochasticity, plant-model mismatch, and directly account for the effect of future uncertainty and its feedback in a proper closed-loop manner; all without the need of an inner optimization loop. One of the main reasons why reinforcement learning has not been considered for industrial processes (or almost any engineering application) is that it lacks a framework to deal with safety critical constraints. Present algorithms for policy optimization use difficult-to-tune penalty parameters, fail to reliably satisfy state constraints or present guarantees only in expectation. We propose a chance constrained policy optimization (CCPO) algorithm which guarantees the satisfaction of joint chance constraints with a high probability - which is crucial for safety critical tasks. This is achieved by the introduction of constraint tightening (backoffs), which are computed simultaneously with the feedback policy. Backoffs are adjusted with Bayesian optimization using the empirical cumulative distribution function of the probabilistic constraints, and are therefore self-tuned. This results in a general methodology that can be imbued into present policy optimization algorithms to enable them to satisfy joint chance constraints with high probability. We present case studies that analyze the performance of the proposed approach.