Ilya Orson Sandoval
An Attentive Graph Agent for Topology-Adaptive Cyber Defence
Jan 24, 2025Abstract:As cyber threats grow increasingly sophisticated, reinforcement learning is emerging as a promising technique to create intelligent, self-improving defensive systems. However, most existing autonomous defensive agents have overlooked the inherent graph structure of computer networks subject to cyber attacks, potentially missing critical information. To address this gap, we developed a custom version of the Cyber Operations Research Gym (CybORG) environment that encodes the observable network state as a directed graph, utilizing realistic and interpretable low-level features. %, like number of open ports and unexpected detected connections. We leverage a Graph Attention Network (GAT) architecture to process node, edge, and global features, and modify its output to be compatible with policy gradient methods in reinforcement learning. GAT policies offer several advantages over standard approaches based on simplistic flattened state observations. They can handle the changes in network topology that occur at runtime when dynamic connections between hosts appear. Policies can be deployed to networks that differ in size to the ones seen during training, enabling a degree of generalisation inaccessible with alternative approaches. Furthermore, the graph neural network policies outputs are explainable in terms of tangible network properties, providing enhanced interpretability of defensive actions. We verify that our low-level graph observations are meaningful enough to train GAT defensive policies that are able to adapt to changing topologies. We evaluate how our trained policies perform when deployed on networks of varying sizes with the same subnetwork structure, comparing them against policies specifically trained for each network configuration. Our study contributes to the development of robust cyber defence systems that can better adapt to real-world network security challenges.
Neural ODEs as Feedback Policies for Nonlinear Optimal Control
Oct 20, 2022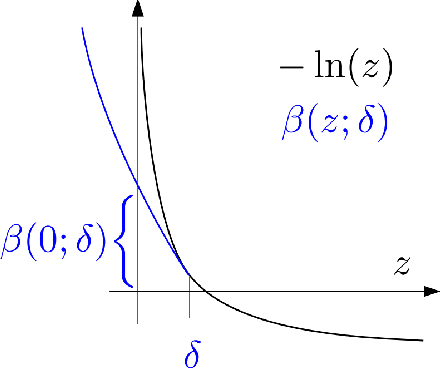
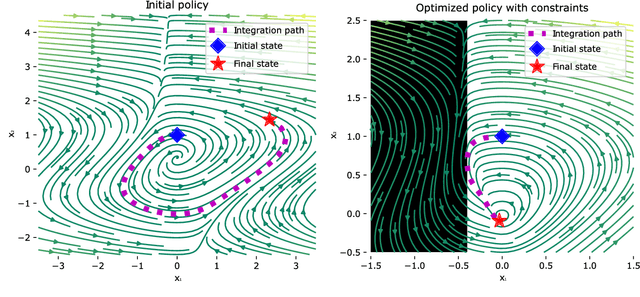

Abstract:Neural ordinary differential equations (Neural ODEs) model continuous time dynamics as differential equations parametrized with neural networks. Thanks to their modeling flexibility, they have been adopted for multiple tasks where the continuous time nature of the process is specially relevant, as in system identification and time series analysis. When applied in a control setting, it is possible to adapt their use to approximate optimal nonlinear feedback policies. This formulation follows the same approach as policy gradients in reinforcement learning, covering the case where the environment consists of known deterministic dynamics given by a system of differential equations. The white box nature of the model specification allows the direct calculation of policy gradients through sensitivity analysis, avoiding the inexact and inefficient gradient estimation through sampling. In this work we propose the use of a neural control policy posed as a Neural ODE to solve general nonlinear optimal control problems while satisfying both state and control constraints, which are crucial for real world scenarios. Since the state feedback policy partially modifies the model dynamics, the whole space phase of the system is reshaped upon the optimization. This approach is a sensible approximation to the historically intractable closed loop solution of nonlinear control problems that efficiently exploits the availability of a dynamical system model.
Chance Constrained Policy Optimization for Process Control and Optimization
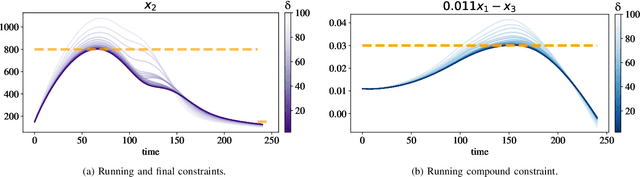
Jul 30, 2020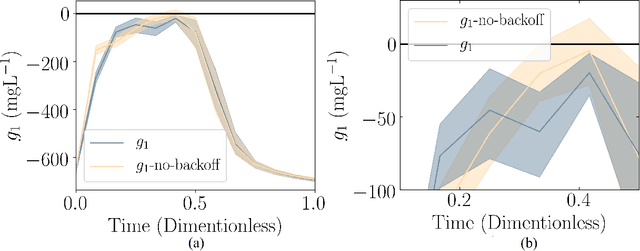

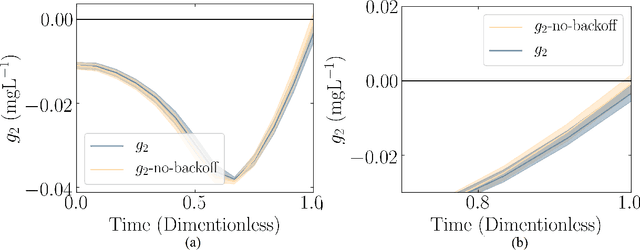
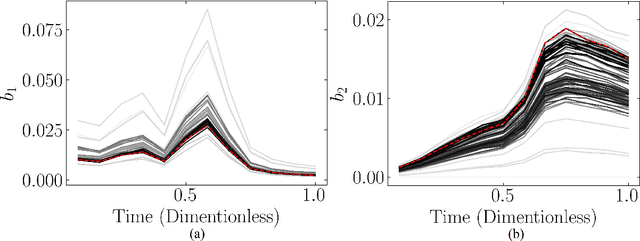
Abstract:Chemical process optimization and control are affected by 1) plant-model mismatch, 2) process disturbances, and 3) constraints for safe operation. Reinforcement learning by policy optimization would be a natural way to solve this due to its ability to address stochasticity, plant-model mismatch, and directly account for the effect of future uncertainty and its feedback in a proper closed-loop manner; all without the need of an inner optimization loop. One of the main reasons why reinforcement learning has not been considered for industrial processes (or almost any engineering application) is that it lacks a framework to deal with safety critical constraints. Present algorithms for policy optimization use difficult-to-tune penalty parameters, fail to reliably satisfy state constraints or present guarantees only in expectation. We propose a chance constrained policy optimization (CCPO) algorithm which guarantees the satisfaction of joint chance constraints with a high probability - which is crucial for safety critical tasks. This is achieved by the introduction of constraint tightening (backoffs), which are computed simultaneously with the feedback policy. Backoffs are adjusted with Bayesian optimization using the empirical cumulative distribution function of the probabilistic constraints, and are therefore self-tuned. This results in a general methodology that can be imbued into present policy optimization algorithms to enable them to satisfy joint chance constraints with high probability. We present case studies that analyze the performance of the proposed approach.
Constrained Reinforcement Learning for Dynamic Optimization under Uncertainty
Jun 04, 2020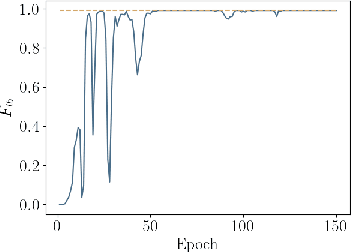
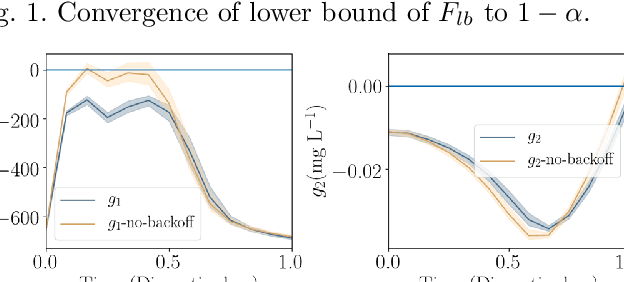
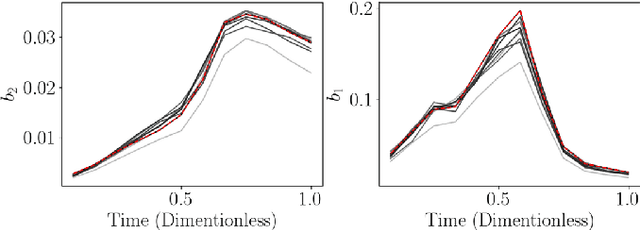

Abstract:Dynamic real-time optimization (DRTO) is a challenging task due to the fact that optimal operating conditions must be computed in real time. The main bottleneck in the industrial application of DRTO is the presence of uncertainty. Many stochastic systems present the following obstacles: 1) plant-model mismatch, 2) process disturbances, 3) risks in violation of process constraints. To accommodate these difficulties, we present a constrained reinforcement learning (RL) based approach. RL naturally handles the process uncertainty by computing an optimal feedback policy. However, no state constraints can be introduced intuitively. To address this problem, we present a chance-constrained RL methodology. We use chance constraints to guarantee the probabilistic satisfaction of process constraints, which is accomplished by introducing backoffs, such that the optimal policy and backoffs are computed simultaneously. Backoffs are adjusted using the empirical cumulative distribution function to guarantee the satisfaction of a joint chance constraint. The advantage and performance of this strategy are illustrated through a stochastic dynamic bioprocess optimization problem, to produce sustainable high-value bioproducts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge