Integrating knowledge-guided symbolic regression and model-based design of experiments to automate process flow diagram development

New products must be formulated rapidly to succeed in the global formulated product market; however, key product indicators (KPIs) can be complex, poorly understood functions of the chemical composition and processing history. Consequently, scale-up must currently undergo expensive trial-and-error campaigns. To accelerate process flow diagram (PFD) optimisation and knowledge discovery, this work proposed a novel digital framework to automatically quantify process mechanisms by integrating symbolic regression (SR) within model-based design of experiments (MBDoE). Each iteration, SR proposed a Pareto front of interpretable mechanistic expressions, and then MBDoE designed a new experiment to discriminate between them while balancing PFD optimisation. To investigate the framework's performance, a new process model capable of simulating general formulated product synthesis was constructed to generate in-silico data for different case studies. The framework could effectively discover ground-truth process mechanisms within a few iterations, indicating its great potential for use within the general chemical industry for digital manufacturing and product innovation.

Distributional Reinforcement Learning for Scheduling of Chemical Production Processes

Reinforcement Learning (RL) has recently received significant attention from the process systems engineering and control communities. Recent works have investigated the application of RL to identify optimal scheduling decision in the presence of uncertainty. In this work, we present a RL methodology tailored to efficiently address production scheduling problems in the presence of uncertainty. We consider commonly imposed restrictions on these problems such as precedence and disjunctive constraints which are not naturally considered by RL in other contexts. Additionally, this work naturally enables the optimization of risk-sensitive formulations such as the conditional value-at-risk (CVaR), which are essential in realistic scheduling processes. The proposed strategy is investigated thoroughly in a parallel batch production environment, and benchmarked against mixed integer linear programming (MILP) strategies. We show that the policy identified by our approach is able to account for plant uncertainties in online decision-making, with expected performance comparable to existing MILP methods. Additionally, the framework gains the benefits of optimizing for risk-sensitive measures, and identifies online decisions orders of magnitude faster than the most efficient optimization approaches. This promises to mitigate practical issues and ease in handling realizations of process uncertainty in the paradigm of online production scheduling.

Safe Chance Constrained Reinforcement Learning for Batch Process Control

Reinforcement Learning (RL) controllers have generated excitement within the control community. The primary advantage of RL controllers relative to existing methods is their ability to optimize uncertain systems independently of explicit assumption of process uncertainty. Recent focus on engineering applications has been directed towards the development of safe RL controllers. Previous works have proposed approaches to account for constraint satisfaction through constraint tightening from the domain of stochastic model predictive control. Here, we extend these approaches to account for plant-model mismatch. Specifically, we propose a data-driven approach that utilizes Gaussian processes for the offline simulation model and use the associated posterior uncertainty prediction to account for joint chance constraints and plant-model mismatch. The method is benchmarked against nonlinear model predictive control via case studies. The results demonstrate the ability of the methodology to account for process uncertainty, enabling satisfaction of joint chance constraints even in the presence of plant-model mismatch.

Constrained Model-Free Reinforcement Learning for Process Optimization

Reinforcement learning (RL) is a control approach that can handle nonlinear stochastic optimal control problems. However, despite the promise exhibited, RL has yet to see marked translation to industrial practice primarily due to its inability to satisfy state constraints. In this work we aim to address this challenge. We propose an 'oracle'-assisted constrained Q-learning algorithm that guarantees the satisfaction of joint chance constraints with a high probability, which is crucial for safety critical tasks. To achieve this, constraint tightening (backoffs) are introduced and adjusted using Broyden's method, hence making them self-tuned. This results in a general methodology that can be imbued into approximate dynamic programming-based algorithms to ensure constraint satisfaction with high probability. Finally, we present case studies that analyze the performance of the proposed approach and compare this algorithm with model predictive control (MPC). The favorable performance of this algorithm signifies a step toward the incorporation of RL into real world optimization and control of engineering systems, where constraints are essential in ensuring safety.

Chance Constrained Policy Optimization for Process Control and Optimization

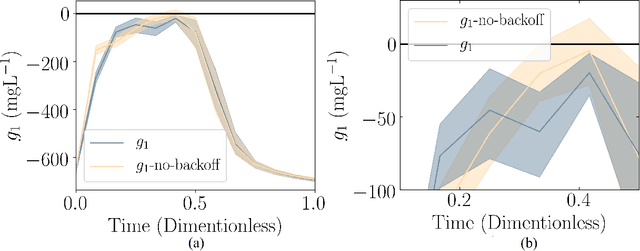
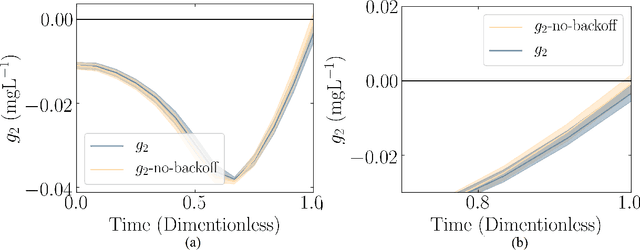
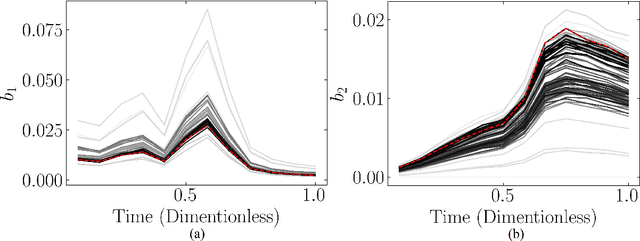
Chemical process optimization and control are affected by 1) plant-model mismatch, 2) process disturbances, and 3) constraints for safe operation. Reinforcement learning by policy optimization would be a natural way to solve this due to its ability to address stochasticity, plant-model mismatch, and directly account for the effect of future uncertainty and its feedback in a proper closed-loop manner; all without the need of an inner optimization loop. One of the main reasons why reinforcement learning has not been considered for industrial processes (or almost any engineering application) is that it lacks a framework to deal with safety critical constraints. Present algorithms for policy optimization use difficult-to-tune penalty parameters, fail to reliably satisfy state constraints or present guarantees only in expectation. We propose a chance constrained policy optimization (CCPO) algorithm which guarantees the satisfaction of joint chance constraints with a high probability - which is crucial for safety critical tasks. This is achieved by the introduction of constraint tightening (backoffs), which are computed simultaneously with the feedback policy. Backoffs are adjusted with Bayesian optimization using the empirical cumulative distribution function of the probabilistic constraints, and are therefore self-tuned. This results in a general methodology that can be imbued into present policy optimization algorithms to enable them to satisfy joint chance constraints with high probability. We present case studies that analyze the performance of the proposed approach.

Constrained Reinforcement Learning for Dynamic Optimization under Uncertainty

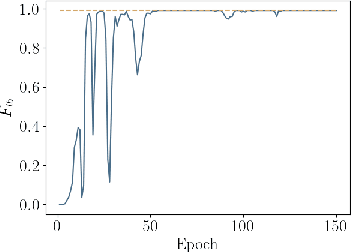
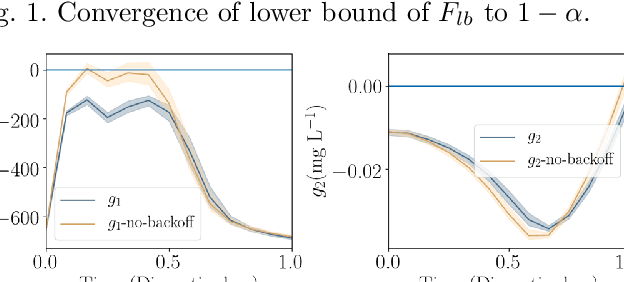
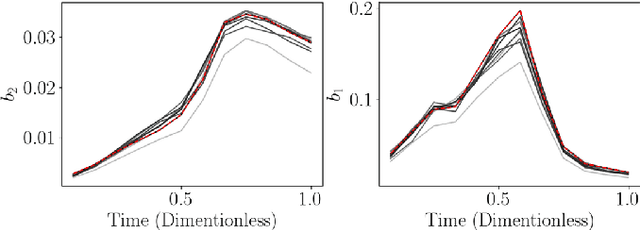
Dynamic real-time optimization (DRTO) is a challenging task due to the fact that optimal operating conditions must be computed in real time. The main bottleneck in the industrial application of DRTO is the presence of uncertainty. Many stochastic systems present the following obstacles: 1) plant-model mismatch, 2) process disturbances, 3) risks in violation of process constraints. To accommodate these difficulties, we present a constrained reinforcement learning (RL) based approach. RL naturally handles the process uncertainty by computing an optimal feedback policy. However, no state constraints can be introduced intuitively. To address this problem, we present a chance-constrained RL methodology. We use chance constraints to guarantee the probabilistic satisfaction of process constraints, which is accomplished by introducing backoffs, such that the optimal policy and backoffs are computed simultaneously. Backoffs are adjusted using the empirical cumulative distribution function to guarantee the satisfaction of a joint chance constraint. The advantage and performance of this strategy are illustrated through a stochastic dynamic bioprocess optimization problem, to produce sustainable high-value bioproducts.

Stochastic data-driven model predictive control using Gaussian processes

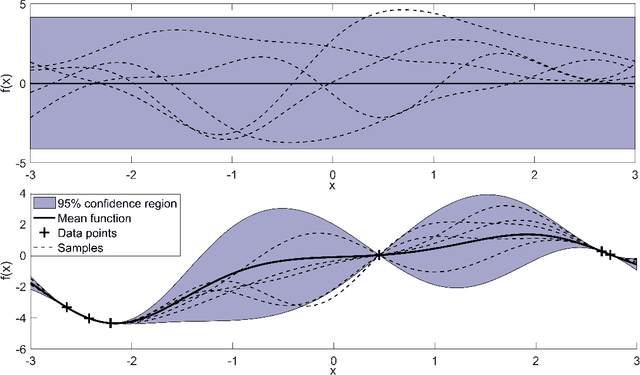
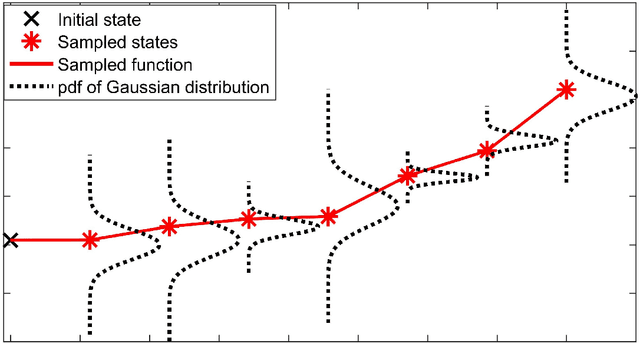
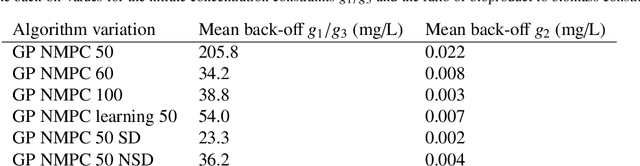
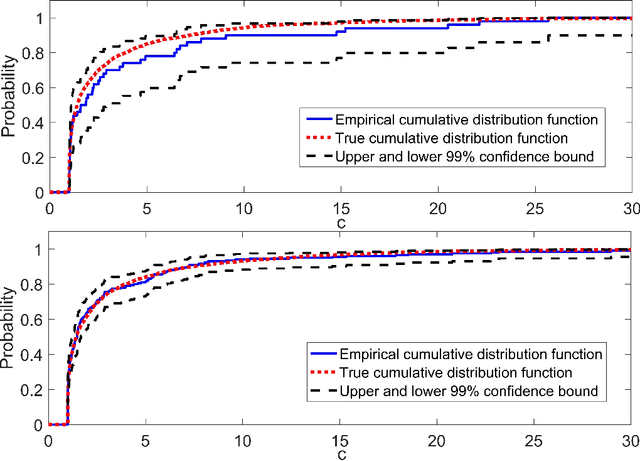
Nonlinear model predictive control (NMPC) is one of the few control methods that can handle multivariable nonlinear control systems with constraints. Gaussian processes (GPs) present a powerful tool to identify the required plant model and quantify the residual uncertainty of the plant-model mismatch given its probabilistic nature . It is crucial to account for this uncertainty, since it may lead to worse control performance and constraint violations. In this paper we propose a new method to design a GP-based NMPC algorithm for finite horizon control problems. The method generates Monte Carlo samples of the GP offline for constraint tightening using back-offs. The tightened constraints then guarantee the satisfaction of joint chance constraints online. Advantages of our proposed approach over existing methods include fast online evaluation time, consideration of closed-loop behaviour, and the possibility to alleviate conservativeness by accounting for both online learning and state dependency of the uncertainty. The algorithm is verified on a challenging semi-batch bioprocess case study, with its high performance thoroughly demonstrated.