Modifier Adaptation Meets Bayesian Optimization and Derivative-Free Optimization

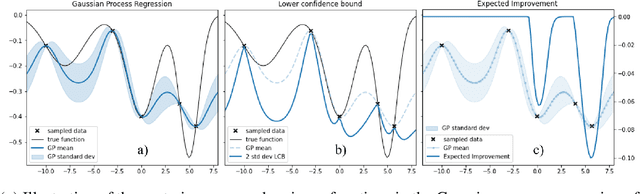
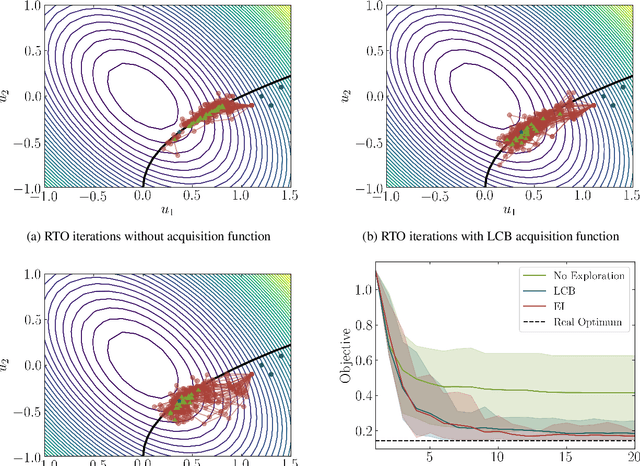
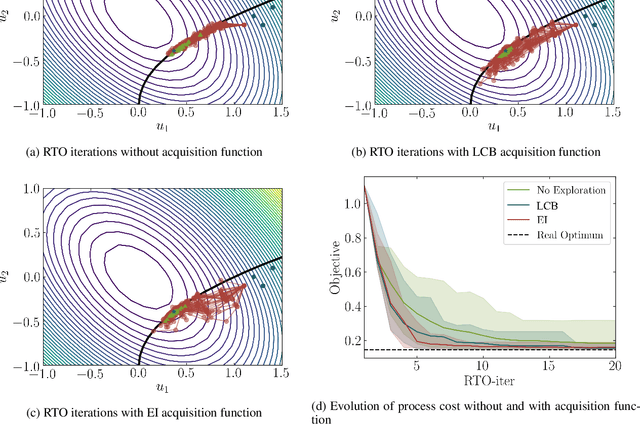
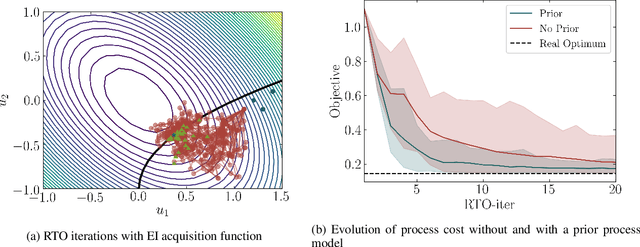
This paper investigates a new class of modifier-adaptation schemes to overcome plant-model mismatch in real-time optimization of uncertain processes. The main contribution lies in the integration of concepts from the areas of Bayesian optimization and derivative-free optimization. The proposed schemes embed a physical model and rely on trust-region ideas to minimize risk during the exploration, while employing Gaussian process regression to capture the plant-model mismatch in a non-parametric way and drive the exploration by means of acquisition functions. The benefits of using an acquisition function, knowing the process noise level, or specifying a nominal process model are illustrated on numerical case studies, including a semi-batch photobioreactor optimization problem.

Chance Constrained Policy Optimization for Process Control and Optimization

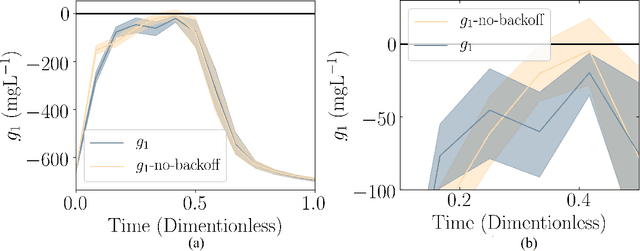
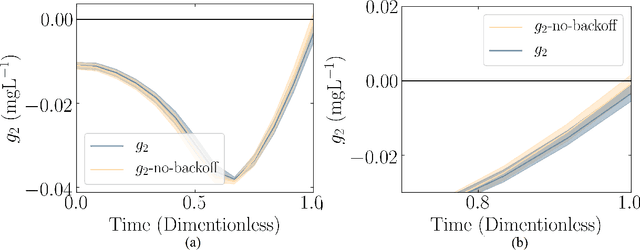
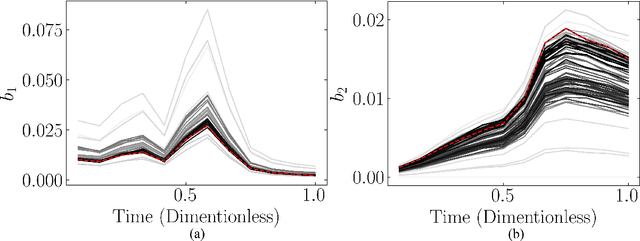
Chemical process optimization and control are affected by 1) plant-model mismatch, 2) process disturbances, and 3) constraints for safe operation. Reinforcement learning by policy optimization would be a natural way to solve this due to its ability to address stochasticity, plant-model mismatch, and directly account for the effect of future uncertainty and its feedback in a proper closed-loop manner; all without the need of an inner optimization loop. One of the main reasons why reinforcement learning has not been considered for industrial processes (or almost any engineering application) is that it lacks a framework to deal with safety critical constraints. Present algorithms for policy optimization use difficult-to-tune penalty parameters, fail to reliably satisfy state constraints or present guarantees only in expectation. We propose a chance constrained policy optimization (CCPO) algorithm which guarantees the satisfaction of joint chance constraints with a high probability - which is crucial for safety critical tasks. This is achieved by the introduction of constraint tightening (backoffs), which are computed simultaneously with the feedback policy. Backoffs are adjusted with Bayesian optimization using the empirical cumulative distribution function of the probabilistic constraints, and are therefore self-tuned. This results in a general methodology that can be imbued into present policy optimization algorithms to enable them to satisfy joint chance constraints with high probability. We present case studies that analyze the performance of the proposed approach.

Constrained Reinforcement Learning for Dynamic Optimization under Uncertainty

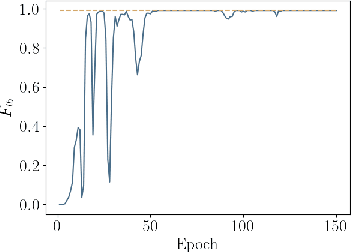
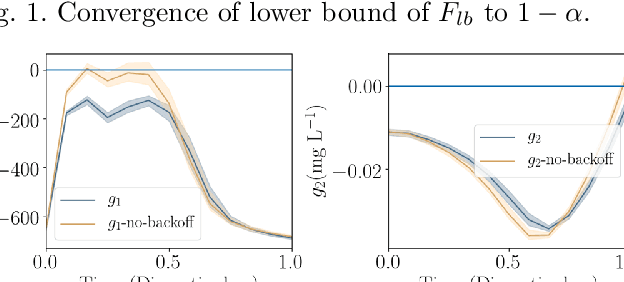
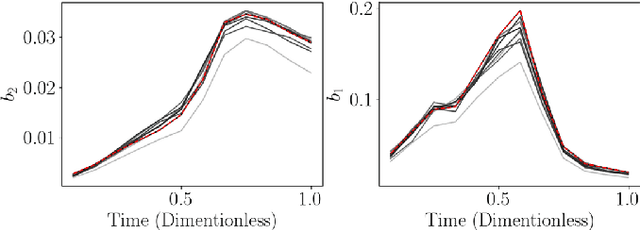
Dynamic real-time optimization (DRTO) is a challenging task due to the fact that optimal operating conditions must be computed in real time. The main bottleneck in the industrial application of DRTO is the presence of uncertainty. Many stochastic systems present the following obstacles: 1) plant-model mismatch, 2) process disturbances, 3) risks in violation of process constraints. To accommodate these difficulties, we present a constrained reinforcement learning (RL) based approach. RL naturally handles the process uncertainty by computing an optimal feedback policy. However, no state constraints can be introduced intuitively. To address this problem, we present a chance-constrained RL methodology. We use chance constraints to guarantee the probabilistic satisfaction of process constraints, which is accomplished by introducing backoffs, such that the optimal policy and backoffs are computed simultaneously. Backoffs are adjusted using the empirical cumulative distribution function to guarantee the satisfaction of a joint chance constraint. The advantage and performance of this strategy are illustrated through a stochastic dynamic bioprocess optimization problem, to produce sustainable high-value bioproducts.

Stochastic data-driven model predictive control using Gaussian processes

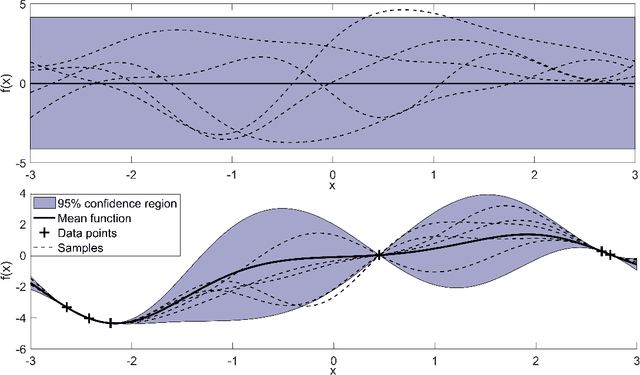
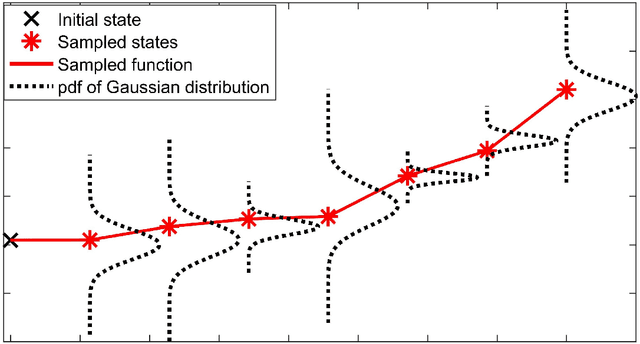
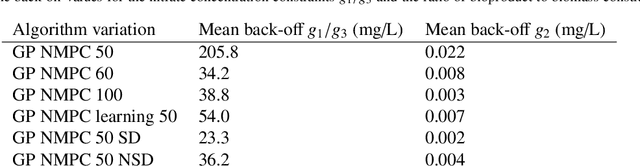
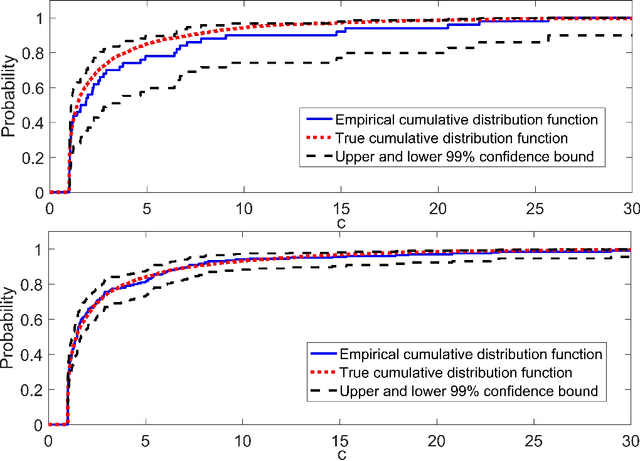
Nonlinear model predictive control (NMPC) is one of the few control methods that can handle multivariable nonlinear control systems with constraints. Gaussian processes (GPs) present a powerful tool to identify the required plant model and quantify the residual uncertainty of the plant-model mismatch given its probabilistic nature . It is crucial to account for this uncertainty, since it may lead to worse control performance and constraint violations. In this paper we propose a new method to design a GP-based NMPC algorithm for finite horizon control problems. The method generates Monte Carlo samples of the GP offline for constraint tightening using back-offs. The tightened constraints then guarantee the satisfaction of joint chance constraints online. Advantages of our proposed approach over existing methods include fast online evaluation time, consideration of closed-loop behaviour, and the possibility to alleviate conservativeness by accounting for both online learning and state dependency of the uncertainty. The algorithm is verified on a challenging semi-batch bioprocess case study, with its high performance thoroughly demonstrated.