Safe Chance Constrained Reinforcement Learning for Batch Process Control

Reinforcement Learning (RL) controllers have generated excitement within the control community. The primary advantage of RL controllers relative to existing methods is their ability to optimize uncertain systems independently of explicit assumption of process uncertainty. Recent focus on engineering applications has been directed towards the development of safe RL controllers. Previous works have proposed approaches to account for constraint satisfaction through constraint tightening from the domain of stochastic model predictive control. Here, we extend these approaches to account for plant-model mismatch. Specifically, we propose a data-driven approach that utilizes Gaussian processes for the offline simulation model and use the associated posterior uncertainty prediction to account for joint chance constraints and plant-model mismatch. The method is benchmarked against nonlinear model predictive control via case studies. The results demonstrate the ability of the methodology to account for process uncertainty, enabling satisfaction of joint chance constraints even in the presence of plant-model mismatch.

Constrained Reinforcement Learning for Dynamic Optimization under Uncertainty

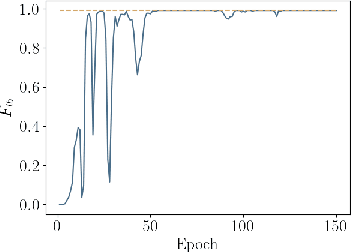
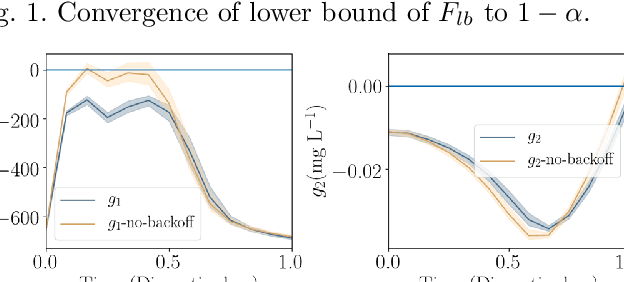
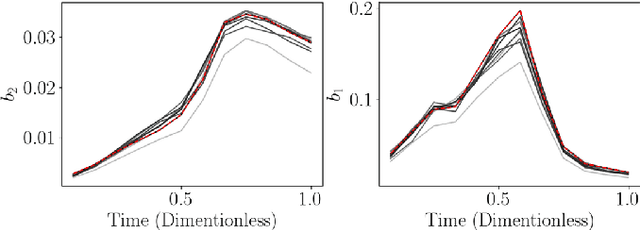
Dynamic real-time optimization (DRTO) is a challenging task due to the fact that optimal operating conditions must be computed in real time. The main bottleneck in the industrial application of DRTO is the presence of uncertainty. Many stochastic systems present the following obstacles: 1) plant-model mismatch, 2) process disturbances, 3) risks in violation of process constraints. To accommodate these difficulties, we present a constrained reinforcement learning (RL) based approach. RL naturally handles the process uncertainty by computing an optimal feedback policy. However, no state constraints can be introduced intuitively. To address this problem, we present a chance-constrained RL methodology. We use chance constraints to guarantee the probabilistic satisfaction of process constraints, which is accomplished by introducing backoffs, such that the optimal policy and backoffs are computed simultaneously. Backoffs are adjusted using the empirical cumulative distribution function to guarantee the satisfaction of a joint chance constraint. The advantage and performance of this strategy are illustrated through a stochastic dynamic bioprocess optimization problem, to produce sustainable high-value bioproducts.