Machine learning for industrial sensing and control: A survey and practical perspective

With the rise of deep learning, there has been renewed interest within the process industries to utilize data on large-scale nonlinear sensing and control problems. We identify key statistical and machine learning techniques that have seen practical success in the process industries. To do so, we start with hybrid modeling to provide a methodological framework underlying core application areas: soft sensing, process optimization, and control. Soft sensing contains a wealth of industrial applications of statistical and machine learning methods. We quantitatively identify research trends, allowing insight into the most successful techniques in practice. We consider two distinct flavors for data-driven optimization and control: hybrid modeling in conjunction with mathematical programming techniques and reinforcement learning. Throughout these application areas, we discuss their respective industrial requirements and challenges. A common challenge is the interpretability and efficiency of purely data-driven methods. This suggests a need to carefully balance deep learning techniques with domain knowledge. As a result, we highlight ways prior knowledge may be integrated into industrial machine learning applications. The treatment of methods, problems, and applications presented here is poised to inform and inspire practitioners and researchers to develop impactful data-driven sensing, optimization, and control solutions in the process industries.

Modern Machine Learning Tools for Monitoring and Control of Industrial Processes: A Survey

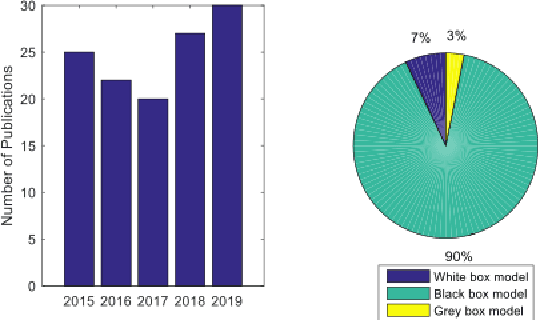
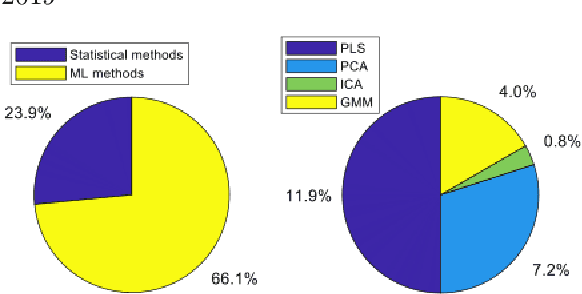
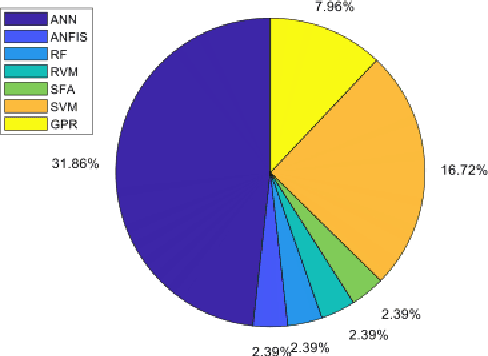
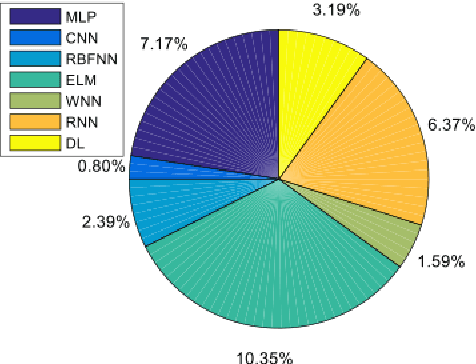
Over the last ten years, we have seen a significant increase in industrial data, tremendous improvement in computational power, and major theoretical advances in machine learning. This opens up an opportunity to use modern machine learning tools on large-scale nonlinear monitoring and control problems. This article provides a survey of recent results with applications in the process industry.

On-line Bayesian parameter estimation in general non-linear state-space models: A tutorial and new results

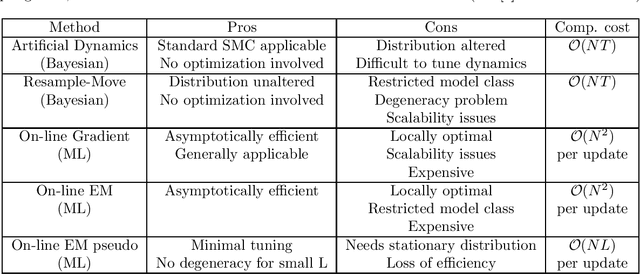
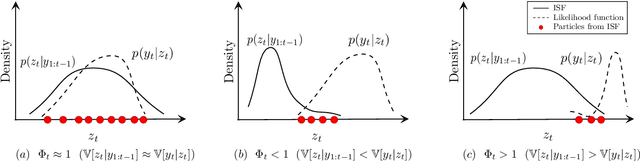
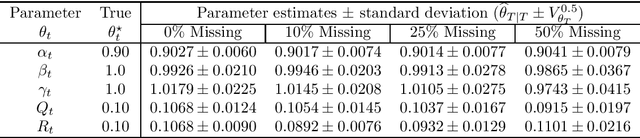
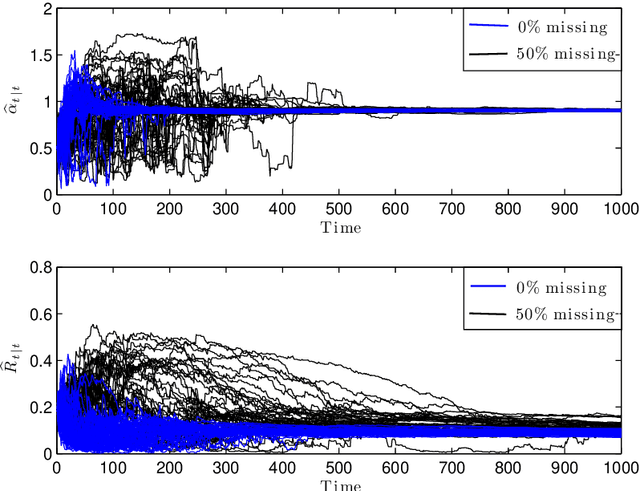
On-line estimation plays an important role in process control and monitoring. Obtaining a theoretical solution to the simultaneous state-parameter estimation problem for non-linear stochastic systems involves solving complex multi-dimensional integrals that are not amenable to analytical solution. While basic sequential Monte-Carlo (SMC) or particle filtering (PF) algorithms for simultaneous estimation exist, it is well recognized that there is a need for making these on-line algorithms non-degenerate, fast and applicable to processes with missing measurements. To overcome the deficiencies in traditional algorithms, this work proposes a Bayesian approach to on-line state and parameter estimation. Its extension to handle missing data in real-time is also provided. The simultaneous estimation is performed by filtering an extended vector of states and parameters using an adaptive sequential-importance-resampling (SIR) filter with a kernel density estimation method. The approach uses an on-line optimization algorithm based on Kullback-Leibler (KL) divergence to allow adaptation of the SIR filter for combined state-parameter estimation. An optimal tuning rule to control the width of the kernel and the variance of the artificial noise added to the parameters is also proposed. The approach is illustrated through numerical examples.