Adaptive Sample Selection for Robust Learning under Label Noise

Deep Neural Networks (DNNs) have been shown to be susceptible to memorization or overfitting in the presence of noisily labelled data. For the problem of robust learning under such noisy data, several algorithms have been proposed. A prominent class of algorithms rely on sample selection strategies, motivated by curriculum learning. For example, many algorithms use the `small loss trick' wherein a fraction of samples with loss values below a certain threshold are selected for training. These algorithms are sensitive to such thresholds, and it is difficult to fix or learn these thresholds. Often, these algorithms also require information such as label noise rates which are typically unavailable in practice. In this paper, we propose a data-dependent, adaptive sample selection strategy that relies only on batch statistics of a given mini-batch to provide robustness against label noise. The algorithm does not have any additional hyperparameters for sample selection, does not need any information on noise rates, and does not need access to separate data with clean labels. We empirically demonstrate the effectiveness of our algorithm on benchmark datasets.

Memorization in Deep Neural Networks: Does the Loss Function matter?

Deep Neural Networks, often owing to the overparameterization, are shown to be capable of exactly memorizing even randomly labelled data. Empirical studies have also shown that none of the standard regularization techniques mitigate such overfitting. We investigate whether the choice of the loss function can affect this memorization. We empirically show, with benchmark data sets MNIST and CIFAR-10, that a symmetric loss function, as opposed to either cross-entropy or squared error loss, results in significant improvement in the ability of the network to resist such overfitting. We then provide a formal definition for robustness to memorization and provide a theoretical explanation as to why the symmetric losses provide this robustness. Our results clearly bring out the role loss functions alone can play in this phenomenon of memorization.

PLUME: Polyhedral Learning Using Mixture of Experts

In this paper, we propose a novel mixture of expert architecture for learning polyhedral classifiers. We learn the parameters of the classifierusing an expectation maximization algorithm. Wederive the generalization bounds of the proposedapproach. Through an extensive simulation study, we show that the proposed method performs comparably to other state-of-the-art approaches.

Efficient Learning of Restricted Boltzmann Machines Using Covariance estimates

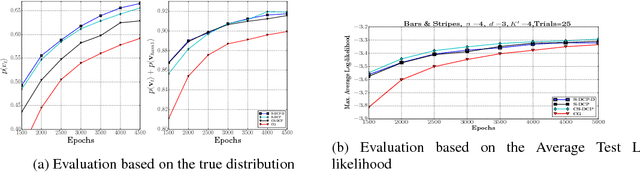
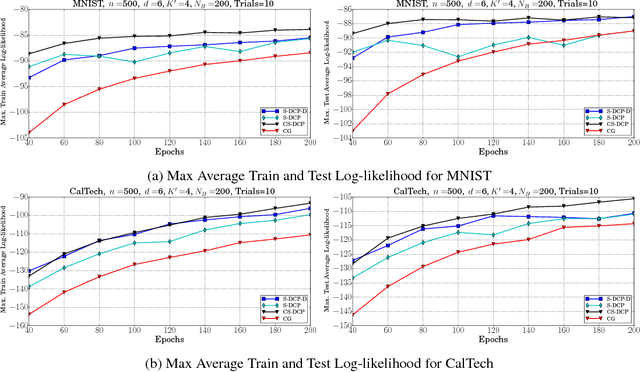
Learning of RBMs using standard algorithms such as CD(k) involves gradient descent on negative log-likelihood. One of the terms in the gradient, which is expectation of visible and hidden units is intractable and is obtained through an MCMC estimate. In this work we show that the Hessian of the log-likelihood can be written in terms of covariances of hidden and visible units and hence all elements of the Hessian can also be estimated using the same MCMC samples with minimal extra computational costs. Since inverting the Hessian may be computationally expensive, we propose an algorithm that uses inverse of the diagonal approximation of the Hessian. This essentially results in parameter-specific adaptive learning rates for the gradient descent process. We show that this algorithm improves the efficiency of learning RBMs compared to state-of-art methods. Specifically we show that using the inverse of diagonal approximation of Hessian in the stochastic DC (difference of convex functions) program approach results in very efficient learning of RBMs. We use different evaluation metrics to test the probability distribution learnt by the RBM along with the traditional criterion of average test and train log-likelihood.

Robust Loss Functions under Label Noise for Deep Neural Networks

In many applications of classifier learning, training data suffers from label noise. Deep networks are learned using huge training data where the problem of noisy labels is particularly relevant. The current techniques proposed for learning deep networks under label noise focus on modifying the network architecture and on algorithms for estimating true labels from noisy labels. An alternate approach would be to look for loss functions that are inherently noise-tolerant. For binary classification there exist theoretical results on loss functions that are robust to label noise. In this paper, we provide some sufficient conditions on a loss function so that risk minimization under that loss function would be inherently tolerant to label noise for multiclass classification problems. These results generalize the existing results on noise-tolerant loss functions for binary classification. We study some of the widely used loss functions in deep networks and show that the loss function based on mean absolute value of error is inherently robust to label noise. Thus standard back propagation is enough to learn the true classifier even under label noise. Through experiments, we illustrate the robustness of risk minimization with such loss functions for learning neural networks.

Learning RBM with a DC programming Approach

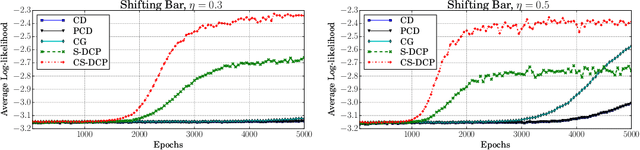
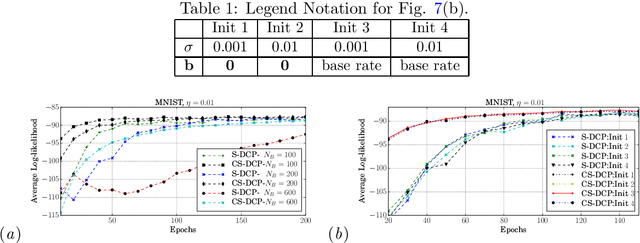
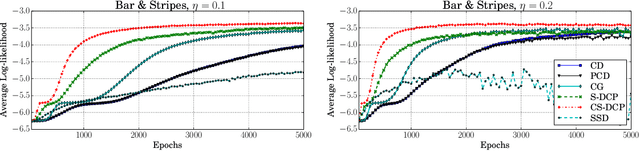
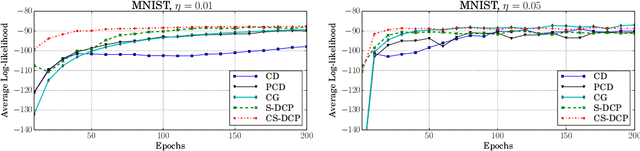
By exploiting the property that the RBM log-likelihood function is the difference of convex functions, we formulate a stochastic variant of the difference of convex functions (DC) programming to minimize the negative log-likelihood. Interestingly, the traditional contrastive divergence algorithm is a special case of the above formulation and the hyperparameters of the two algorithms can be chosen such that the amount of computation per mini-batch is identical. We show that for a given computational budget the proposed algorithm almost always reaches a higher log-likelihood more rapidly, compared to the standard contrastive divergence algorithm. Further, we modify this algorithm to use the centered gradients and show that it is more efficient and effective compared to the standard centered gradient algorithm on benchmark datasets.

On the Robustness of Decision Tree Learning under Label Noise

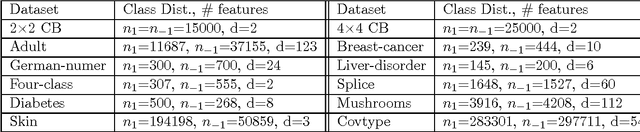
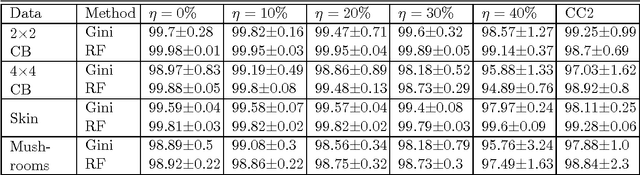
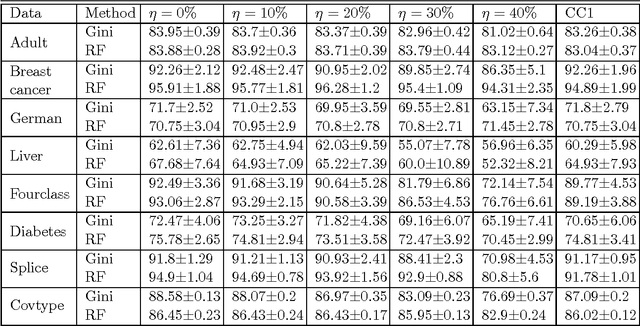
In most practical problems of classifier learning, the training data suffers from the label noise. Hence, it is important to understand how robust is a learning algorithm to such label noise. This paper presents some theoretical analysis to show that many popular decision tree algorithms are robust to symmetric label noise under large sample size. We also present some sample complexity results which provide some bounds on the sample size for the robustness to hold with a high probability. Through extensive simulations we illustrate this robustness.

Empirical Analysis of Sampling Based Estimators for Evaluating RBMs

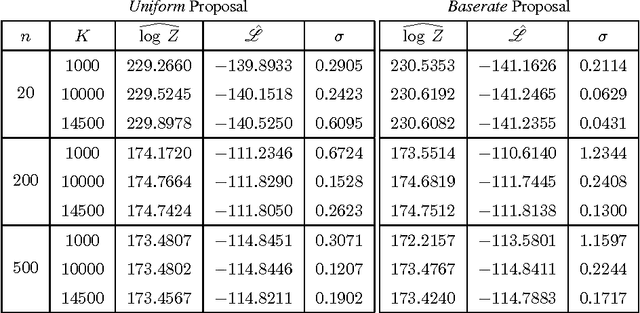
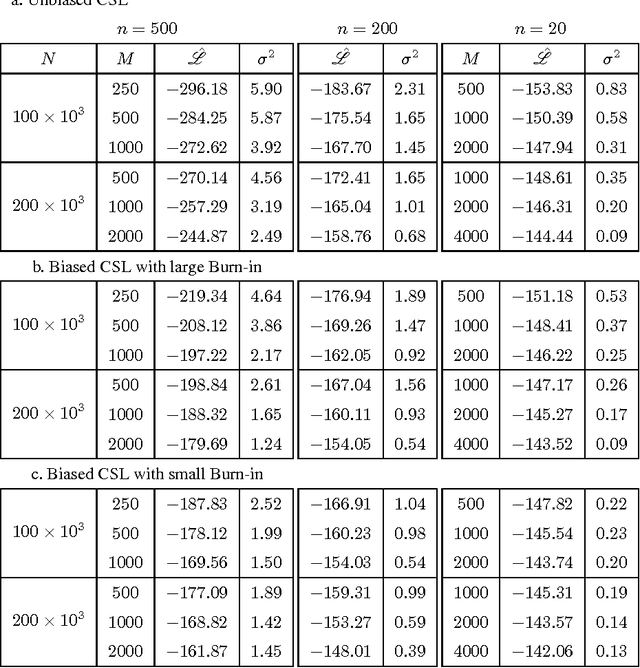
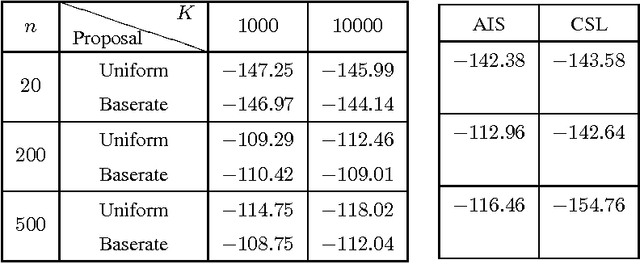
The Restricted Boltzmann Machines (RBM) can be used either as classifiers or as generative models. The quality of the generative RBM is measured through the average log-likelihood on test data. Due to the high computational complexity of evaluating the partition function, exact calculation of test log-likelihood is very difficult. In recent years some estimation methods are suggested for approximate computation of test log-likelihood. In this paper we present an empirical comparison of the main estimation methods, namely, the AIS algorithm for estimating the partition function, the CSL method for directly estimating the log-likelihood, and the RAISE algorithm that combines these two ideas. We use the MNIST data set to learn the RBM and then compare these methods for estimating the test log-likelihood.

Making Risk Minimization Tolerant to Label Noise

In many applications, the training data, from which one needs to learn a classifier, is corrupted with label noise. Many standard algorithms such as SVM perform poorly in presence of label noise. In this paper we investigate the robustness of risk minimization to label noise. We prove a sufficient condition on a loss function for the risk minimization under that loss to be tolerant to uniform label noise. We show that the $0-1$ loss, sigmoid loss, ramp loss and probit loss satisfy this condition though none of the standard convex loss functions satisfy it. We also prove that, by choosing a sufficiently large value of a parameter in the loss function, the sigmoid loss, ramp loss and probit loss can be made tolerant to non-uniform label noise also if we can assume the classes to be separable under noise-free data distribution. Through extensive empirical studies, we show that risk minimization under the $0-1$ loss, the sigmoid loss and the ramp loss has much better robustness to label noise when compared to the SVM algorithm.

Polyceptron: A Polyhedral Learning Algorithm

In this paper we propose a new algorithm for learning polyhedral classifiers which we call as Polyceptron. It is a Perception like algorithm which updates the parameters only when the current classifier misclassifies any training data. We give both batch and online version of Polyceptron algorithm. Finally we give experimental results to show the effectiveness of our approach.