On the Robustness of Decision Tree Learning under Label Noise
Paper and Code
Aug 26, 2016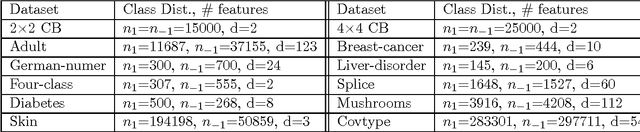
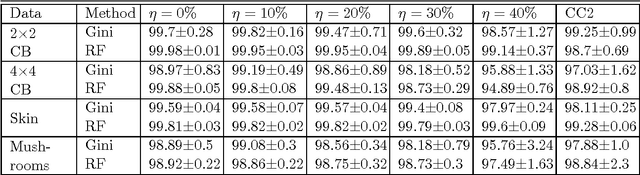
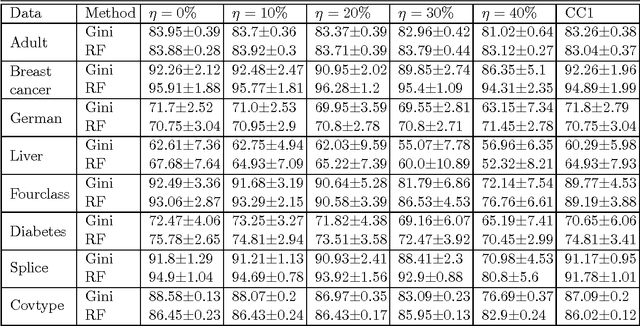
In most practical problems of classifier learning, the training data suffers from the label noise. Hence, it is important to understand how robust is a learning algorithm to such label noise. This paper presents some theoretical analysis to show that many popular decision tree algorithms are robust to symmetric label noise under large sample size. We also present some sample complexity results which provide some bounds on the sample size for the robustness to hold with a high probability. Through extensive simulations we illustrate this robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge