Learning Gaussian-Bernoulli RBMs using Difference of Convex Functions Optimization

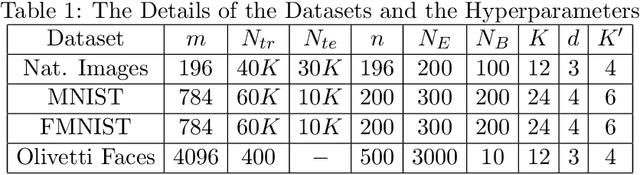
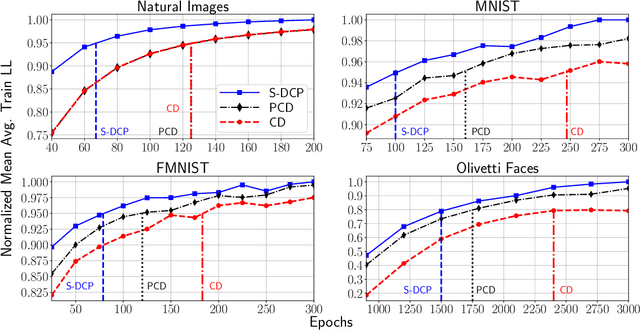
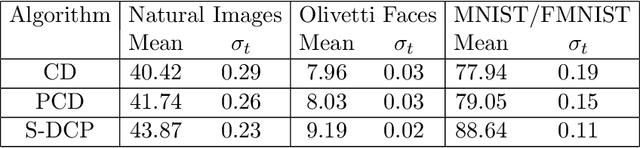
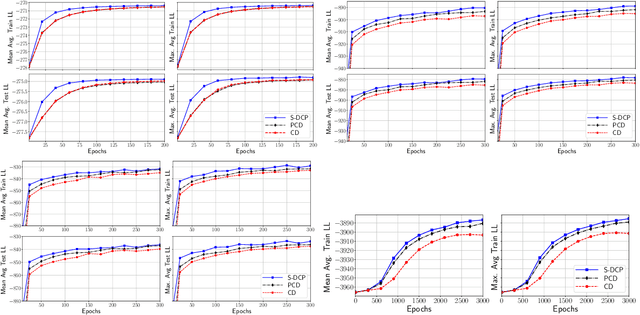
The Gaussian-Bernoulli restricted Boltzmann machine (GB-RBM) is a useful generative model that captures meaningful features from the given $n$-dimensional continuous data. The difficulties associated with learning GB-RBM are reported extensively in earlier studies. They indicate that the training of the GB-RBM using the current standard algorithms, namely, contrastive divergence (CD) and persistent contrastive divergence (PCD), needs a carefully chosen small learning rate to avoid divergence which, in turn, results in slow learning. In this work, we alleviate such difficulties by showing that the negative log-likelihood for a GB-RBM can be expressed as a difference of convex functions if we keep the variance of the conditional distribution of visible units (given hidden unit states) and the biases of the visible units, constant. Using this, we propose a stochastic {\em difference of convex functions} (DC) programming (S-DCP) algorithm for learning the GB-RBM. We present extensive empirical studies on several benchmark datasets to validate the performance of this S-DCP algorithm. It is seen that S-DCP is better than the CD and PCD algorithms in terms of speed of learning and the quality of the generative model learnt.

Efficient Learning of Restricted Boltzmann Machines Using Covariance estimates

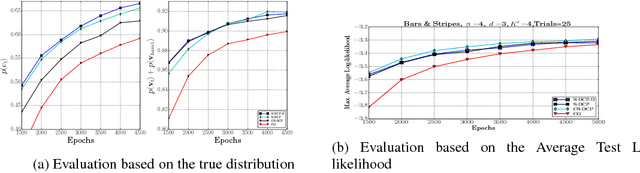
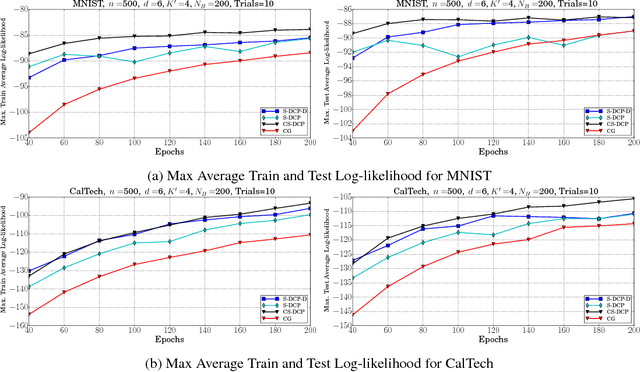
Learning of RBMs using standard algorithms such as CD(k) involves gradient descent on negative log-likelihood. One of the terms in the gradient, which is expectation of visible and hidden units is intractable and is obtained through an MCMC estimate. In this work we show that the Hessian of the log-likelihood can be written in terms of covariances of hidden and visible units and hence all elements of the Hessian can also be estimated using the same MCMC samples with minimal extra computational costs. Since inverting the Hessian may be computationally expensive, we propose an algorithm that uses inverse of the diagonal approximation of the Hessian. This essentially results in parameter-specific adaptive learning rates for the gradient descent process. We show that this algorithm improves the efficiency of learning RBMs compared to state-of-art methods. Specifically we show that using the inverse of diagonal approximation of Hessian in the stochastic DC (difference of convex functions) program approach results in very efficient learning of RBMs. We use different evaluation metrics to test the probability distribution learnt by the RBM along with the traditional criterion of average test and train log-likelihood.

Learning RBM with a DC programming Approach

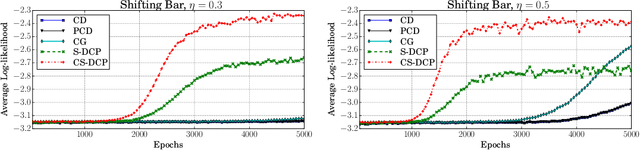
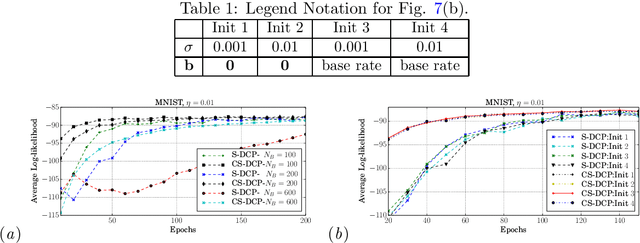
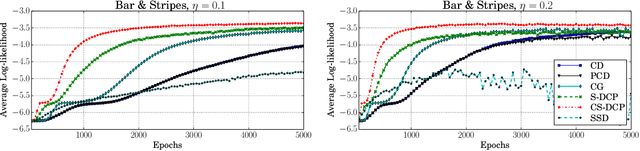
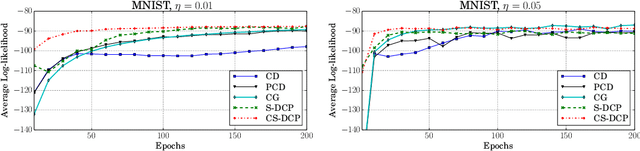
By exploiting the property that the RBM log-likelihood function is the difference of convex functions, we formulate a stochastic variant of the difference of convex functions (DC) programming to minimize the negative log-likelihood. Interestingly, the traditional contrastive divergence algorithm is a special case of the above formulation and the hyperparameters of the two algorithms can be chosen such that the amount of computation per mini-batch is identical. We show that for a given computational budget the proposed algorithm almost always reaches a higher log-likelihood more rapidly, compared to the standard contrastive divergence algorithm. Further, we modify this algorithm to use the centered gradients and show that it is more efficient and effective compared to the standard centered gradient algorithm on benchmark datasets.

Empirical Analysis of Sampling Based Estimators for Evaluating RBMs

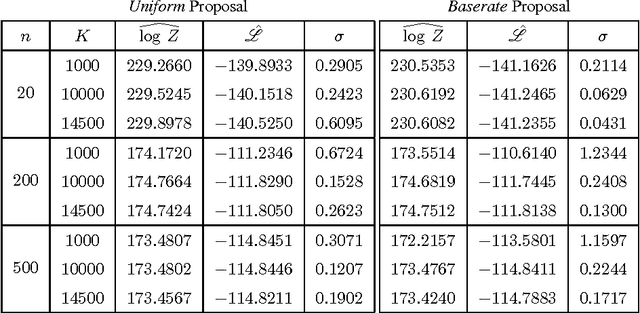
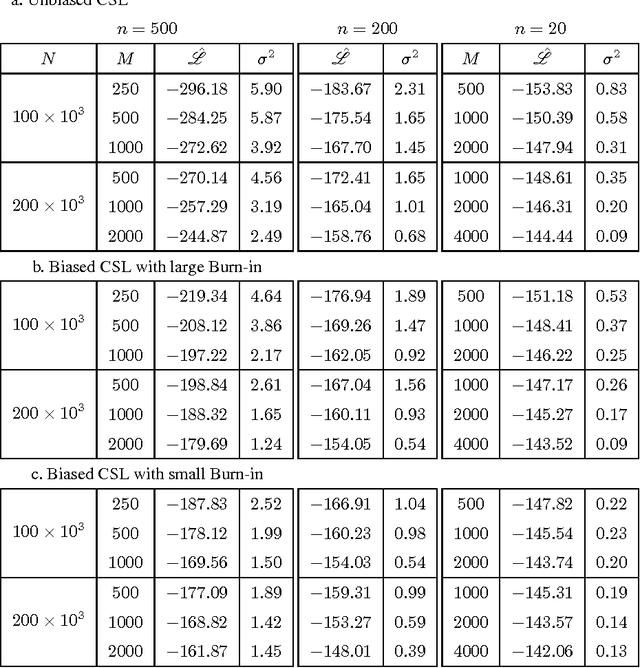
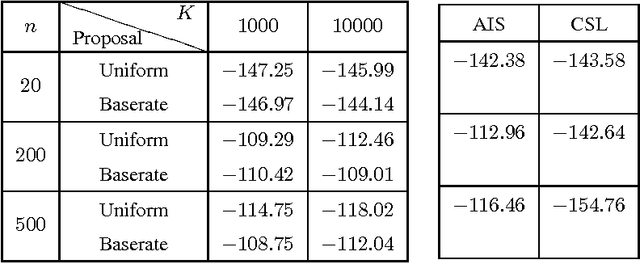
The Restricted Boltzmann Machines (RBM) can be used either as classifiers or as generative models. The quality of the generative RBM is measured through the average log-likelihood on test data. Due to the high computational complexity of evaluating the partition function, exact calculation of test log-likelihood is very difficult. In recent years some estimation methods are suggested for approximate computation of test log-likelihood. In this paper we present an empirical comparison of the main estimation methods, namely, the AIS algorithm for estimating the partition function, the CSL method for directly estimating the log-likelihood, and the RAISE algorithm that combines these two ideas. We use the MNIST data set to learn the RBM and then compare these methods for estimating the test log-likelihood.