Learning Gaussian-Bernoulli RBMs using Difference of Convex Functions Optimization
Paper and Code
Feb 11, 2021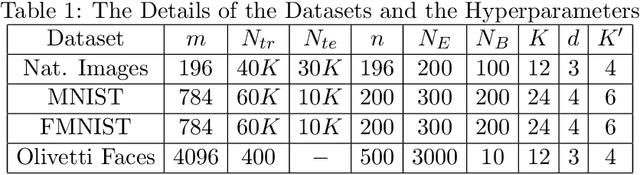
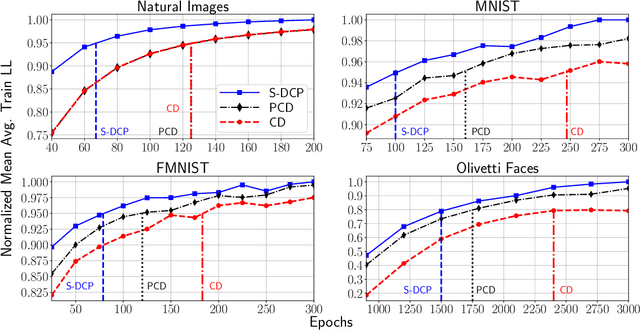
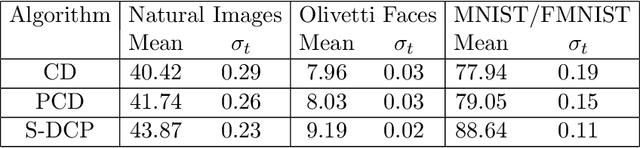
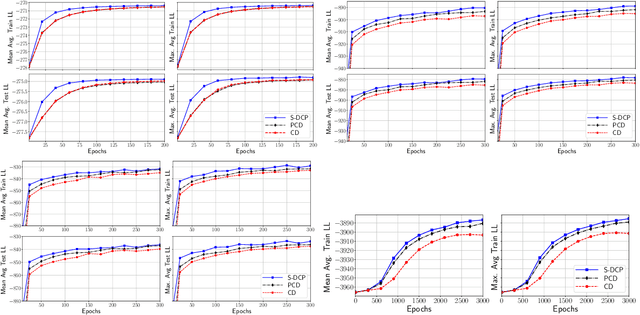
The Gaussian-Bernoulli restricted Boltzmann machine (GB-RBM) is a useful generative model that captures meaningful features from the given $n$-dimensional continuous data. The difficulties associated with learning GB-RBM are reported extensively in earlier studies. They indicate that the training of the GB-RBM using the current standard algorithms, namely, contrastive divergence (CD) and persistent contrastive divergence (PCD), needs a carefully chosen small learning rate to avoid divergence which, in turn, results in slow learning. In this work, we alleviate such difficulties by showing that the negative log-likelihood for a GB-RBM can be expressed as a difference of convex functions if we keep the variance of the conditional distribution of visible units (given hidden unit states) and the biases of the visible units, constant. Using this, we propose a stochastic {\em difference of convex functions} (DC) programming (S-DCP) algorithm for learning the GB-RBM. We present extensive empirical studies on several benchmark datasets to validate the performance of this S-DCP algorithm. It is seen that S-DCP is better than the CD and PCD algorithms in terms of speed of learning and the quality of the generative model learnt.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge