Learning RBM with a DC programming Approach
Paper and Code
Oct 05, 2017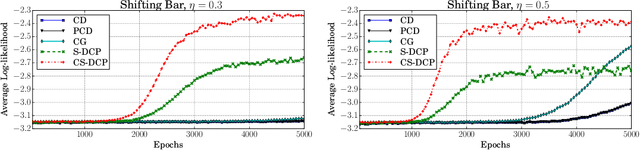
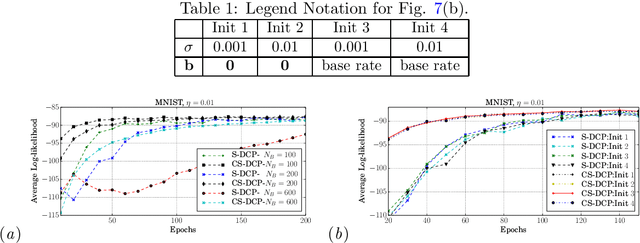
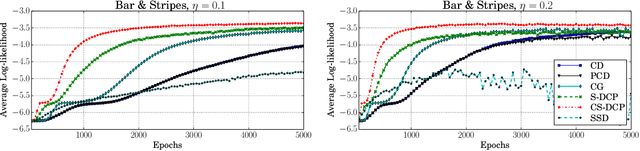
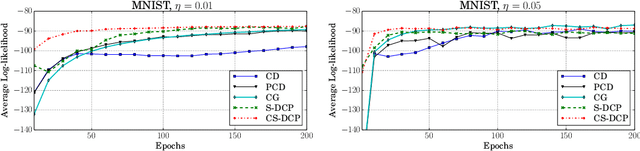
By exploiting the property that the RBM log-likelihood function is the difference of convex functions, we formulate a stochastic variant of the difference of convex functions (DC) programming to minimize the negative log-likelihood. Interestingly, the traditional contrastive divergence algorithm is a special case of the above formulation and the hyperparameters of the two algorithms can be chosen such that the amount of computation per mini-batch is identical. We show that for a given computational budget the proposed algorithm almost always reaches a higher log-likelihood more rapidly, compared to the standard contrastive divergence algorithm. Further, we modify this algorithm to use the centered gradients and show that it is more efficient and effective compared to the standard centered gradient algorithm on benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge