Peer Selection with Noisy Assessments

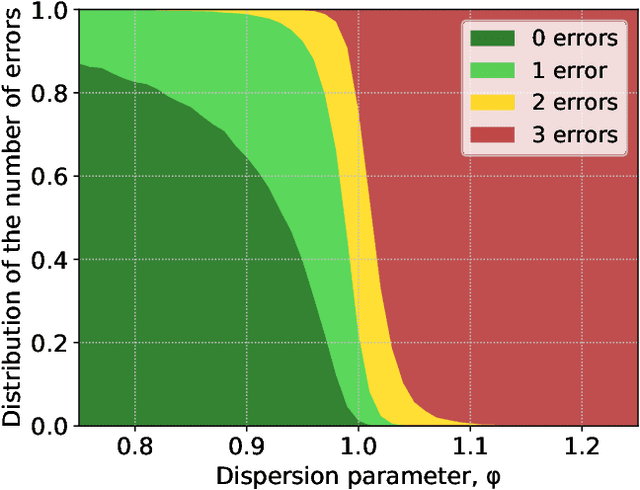
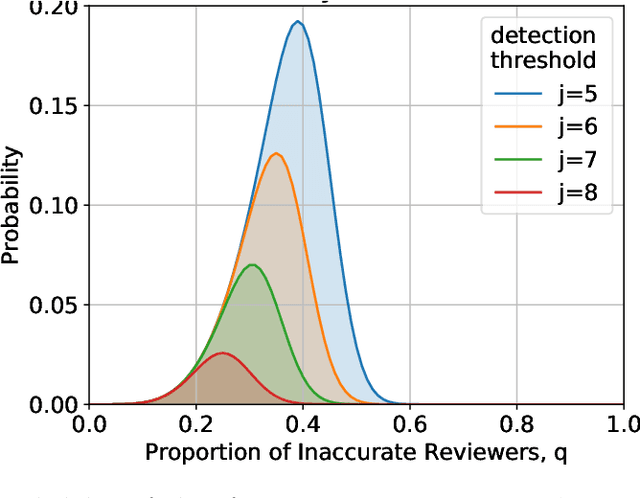
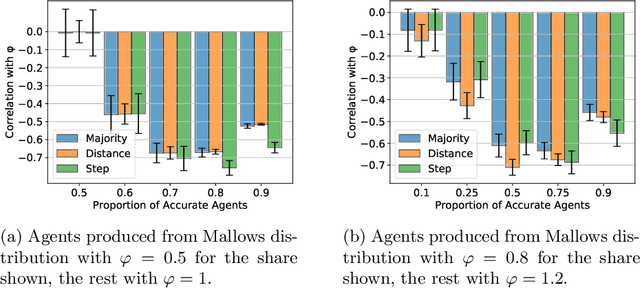
In the peer selection problem a group of agents must select a subset of themselves as winners for, e.g., peer-reviewed grants or prizes. Here, we take a Condorcet view of this aggregation problem, i.e., that there is a ground-truth ordering over the agents and we wish to select the best set of agents, subject to the noisy assessments of the peers. Given this model, some agents may be unreliable, while others might be self-interested, attempting to influence the outcome in their favour. In this paper we extend PeerNomination, the most accurate peer reviewing algorithm to date, into WeightedPeerNomination, which is able to handle noisy and inaccurate agents. To do this, we explicitly formulate assessors' reliability weights in a way that does not violate strategyproofness, and use this information to reweight their scores. We show analytically that a weighting scheme can improve the overall accuracy of the selection significantly. Finally, we implement several instances of reweighting methods and show empirically that our methods are robust in the face of noisy assessments.

The Price is Right: Learning Market Equilibria from Samples

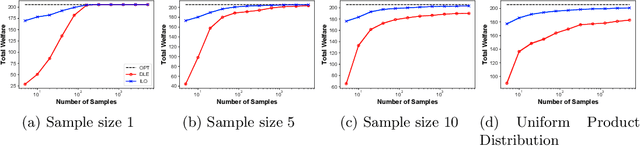
Equilibrium computation in markets usually considers settings where player valuation functions are known. We consider the setting where player valuations are unknown; using a PAC learning-theoretic framework, we analyze some classes of common valuation functions, and provide algorithms which output direct PAC equilibrium allocations, not estimates based on attempting to learn valuation functions. Since there exist trivial PAC market outcomes with an unbounded worst-case efficiency loss, we lower-bound the efficiency of our algorithms. While the efficiency loss under general distributions is rather high, we show that in some cases (e.g., unit-demand valuations), it is possible to find a PAC market equilibrium with significantly better utility.

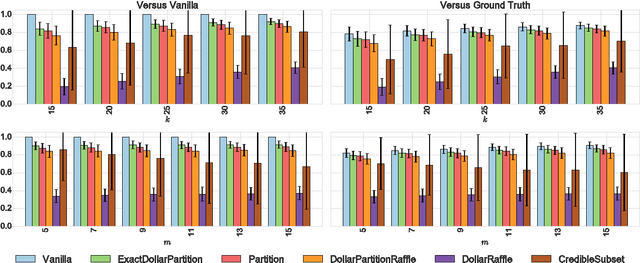
Strategyproof Peer Selection using Randomization, Partitioning, and Apportionment

Peer review, evaluation, and selection is a fundamental aspect of modern science. Funding bodies the world over employ experts to review and select the best proposals of those submitted for funding. The problem of peer selection, however, is much more general: a professional society may want to give a subset of its members awards based on the opinions of all members; an instructor for a MOOC or online course may want to crowdsource grading; or a marketing company may select ideas from group brainstorming sessions based on peer evaluation. We make three fundamental contributions to the study of procedures or mechanisms for peer selection, a specific type of group decision-making problem, studied in computer science, economics, and political science. First, we propose a novel mechanism that is strategyproof, i.e., agents cannot benefit by reporting insincere valuations. Second, we demonstrate the effectiveness of our mechanism by a comprehensive simulation-based comparison with a suite of mechanisms found in the literature. Finally, our mechanism employs a randomized rounding technique that is of independent interest, as it solves the apportionment problem that arises in various settings where discrete resources such as parliamentary representation slots need to be divided proportionally.

Group Recommendations: Axioms, Impossibilities, and Random Walks

We introduce an axiomatic approach to group recommendations, in line of previous work on the axiomatic treatment of trust-based recommendation systems, ranking systems, and other foundational work on the axiomatic approach to internet mechanisms in social choice settings. In group recommendations we wish to recommend to a group of agents, consisting of both opinionated and undecided members, a joint choice that would be acceptable to them. Such a system has many applications, such as choosing a movie or a restaurant to go to with a group of friends, recommending games for online game players, & other communal activities. Our method utilizes a given social graph to extract information on the undecided, relying on the agents influencing them. We first show that a set of fairly natural desired requirements (a.k.a axioms) leads to an impossibility, rendering mutual satisfaction of them unreachable. However, we also show a modified set of axioms that fully axiomatize a group variant of the random-walk recommendation system, expanding a previous result from the individual recommendation case.

An Axiomatic Approach to Routing

Information delivery in a network of agents is a key issue for large, complex systems that need to do so in a predictable, efficient manner. The delivery of information in such multi-agent systems is typically implemented through routing protocols that determine how information flows through the network. Different routing protocols exist each with its own benefits, but it is generally unclear which properties can be successfully combined within a given algorithm. We approach this problem from the axiomatic point of view, i.e., we try to establish what are the properties we would seek to see in such a system, and examine the different properties which uniquely define common routing algorithms used today. We examine several desirable properties, such as robustness, which ensures adding nodes and edges does not change the routing in a radical, unpredictable ways; and properties that depend on the operating environment, such as an "economic model", where nodes choose their paths based on the cost they are charged to pass information to the next node. We proceed to fully characterize minimal spanning tree, shortest path, and weakest link routing algorithms, showing a tight set of axioms for each.