Quantifying Consistency and Information Loss for Causal Abstraction Learning

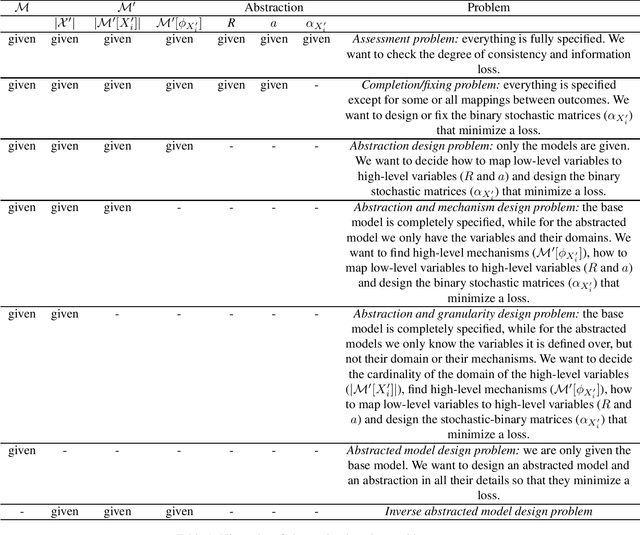
Structural causal models provide a formalism to express causal relations between variables of interest. Models and variables can represent a system at different levels of abstraction, whereby relations may be coarsened and refined according to the need of a modeller. However, switching between different levels of abstraction requires evaluating a trade-off between the consistency and the information loss among different models. In this paper we introduce a family of interventional measures that an agent may use to evaluate such a trade-off. We consider four measures suited for different tasks, analyze their properties, and propose algorithms to evaluate and learn causal abstractions. Finally, we illustrate the flexibility of our setup by empirically showing how different measures and algorithmic choices may lead to different abstractions.

Towards Computing an Optimal Abstraction for Structural Causal Models

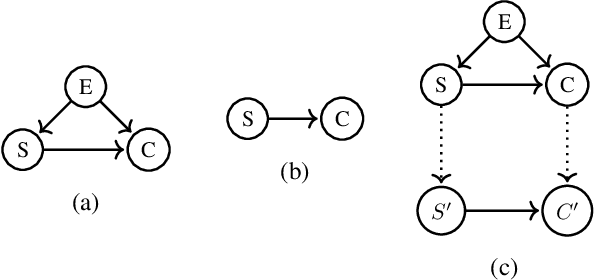
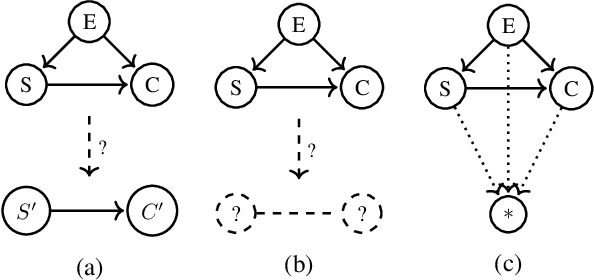
Working with causal models at different levels of abstraction is an important feature of science. Existing work has already considered the problem of expressing formally the relation of abstraction between causal models. In this paper, we focus on the problem of learning abstractions. We start by defining the learning problem formally in terms of the optimization of a standard measure of consistency. We then point out the limitation of this approach, and we suggest extending the objective function with a term accounting for information loss. We suggest a concrete measure of information loss, and we illustrate its contribution to learning new abstractions.

Peer Selection with Noisy Assessments

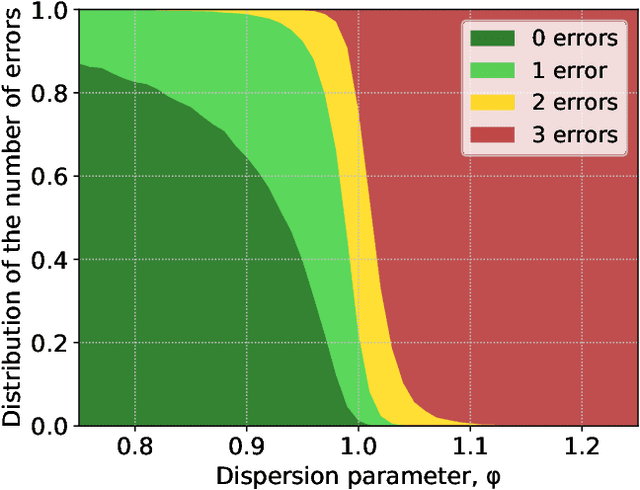
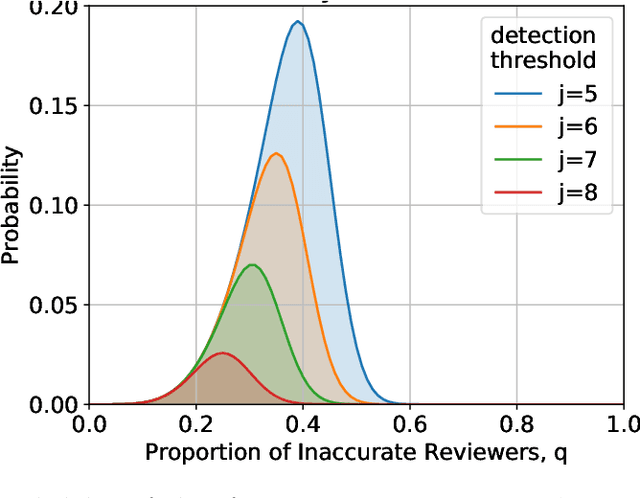
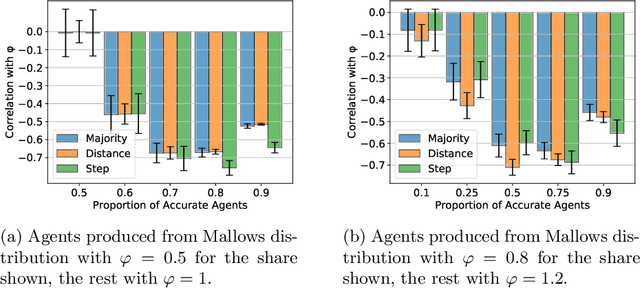
In the peer selection problem a group of agents must select a subset of themselves as winners for, e.g., peer-reviewed grants or prizes. Here, we take a Condorcet view of this aggregation problem, i.e., that there is a ground-truth ordering over the agents and we wish to select the best set of agents, subject to the noisy assessments of the peers. Given this model, some agents may be unreliable, while others might be self-interested, attempting to influence the outcome in their favour. In this paper we extend PeerNomination, the most accurate peer reviewing algorithm to date, into WeightedPeerNomination, which is able to handle noisy and inaccurate agents. To do this, we explicitly formulate assessors' reliability weights in a way that does not violate strategyproofness, and use this information to reweight their scores. We show analytically that a weighting scheme can improve the overall accuracy of the selection significantly. Finally, we implement several instances of reweighting methods and show empirically that our methods are robust in the face of noisy assessments.

PeerNomination: Relaxing Exactness for Increased Accuracy in Peer Selection

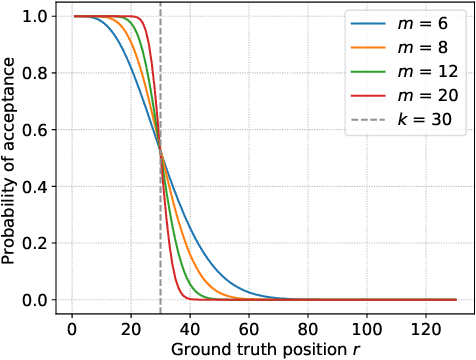
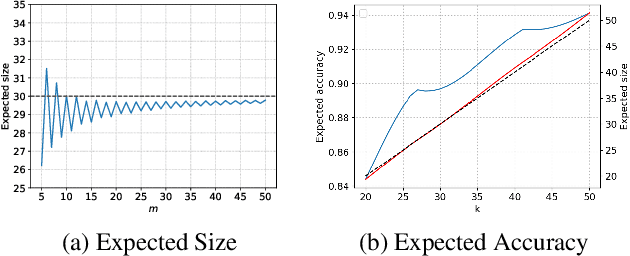
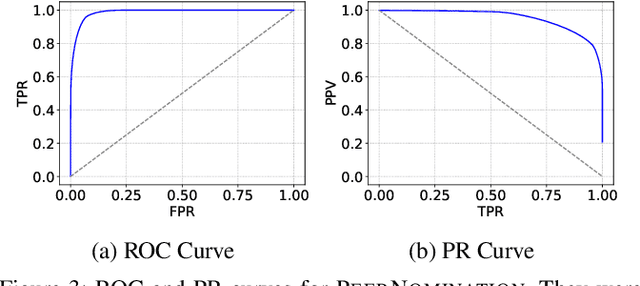
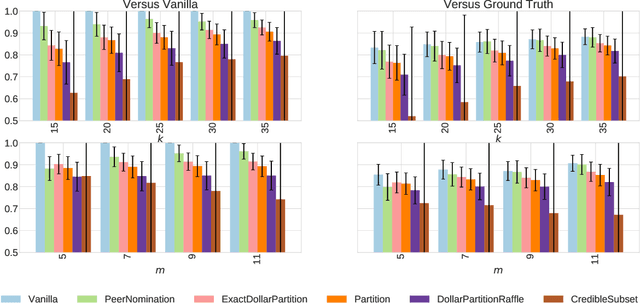
In peer selection agents must choose a subset of themselves for an award or a prize. As agents are self-interested, we want to design algorithms that are impartial, so that an individual agent cannot affect their own chance of being selected. This problem has broad application in resource allocation and mechanism design and has received substantial attention in the artificial intelligence literature. Here, we present a novel algorithm for impartial peer selection, PeerNomination, and provide a theoretical analysis of its accuracy. Our algorithm possesses various desirable features. In particular, it does not require an explicit partitioning of the agents, as previous algorithms in the literature. We show empirically that it achieves higher accuracy than the exiting algorithms over several metrics.

Reducing selfish routing inefficiencies using traffic lights

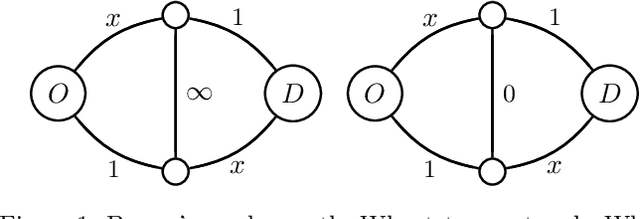
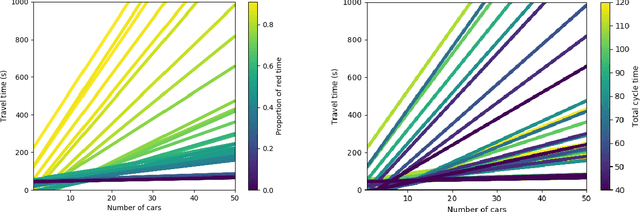
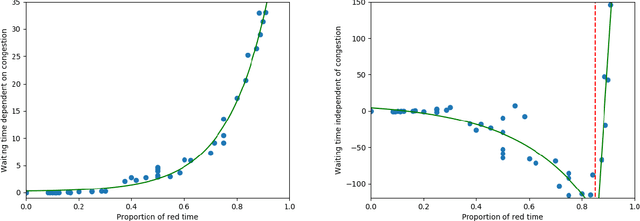
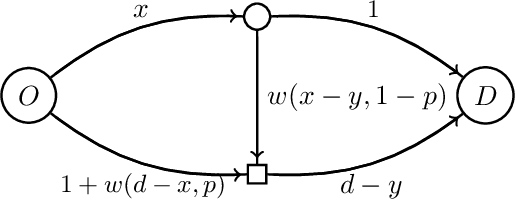
Traffic congestion games abstract away from the costs of junctions in transport networks, yet, in urban environments, these often impact journey times significantly. In this paper we equip congestion games with traffic lights, modelled as junction-based waiting cycles, therefore enabling more realistic route planning strategies. Using the SUMO simulator, we show that our modelling choices coincide with realistic routing behaviours, in particular, that drivers' decisions about route choices are based on the proportion of red light time for their direction of travel. Drawing upon the experimental results, we show that the effects of the notorious Braess' paradox can be avoided in theory and significantly reduced in practice, by allocating the appropriate traffic light cycles along a transport network.

Similarity Measures based on Local Game Trees

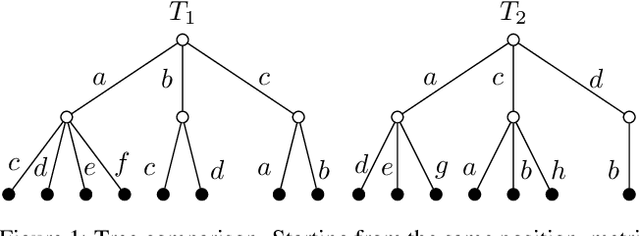
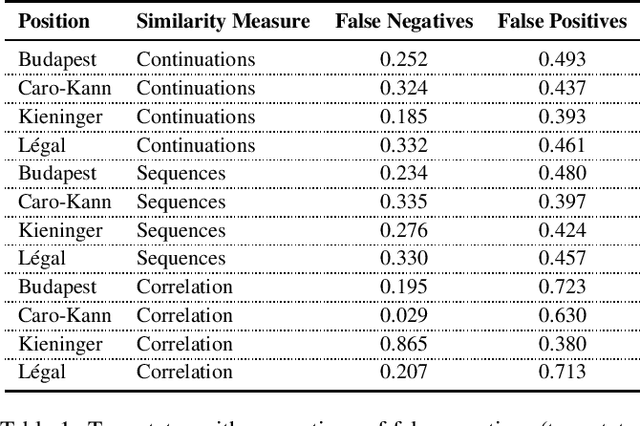
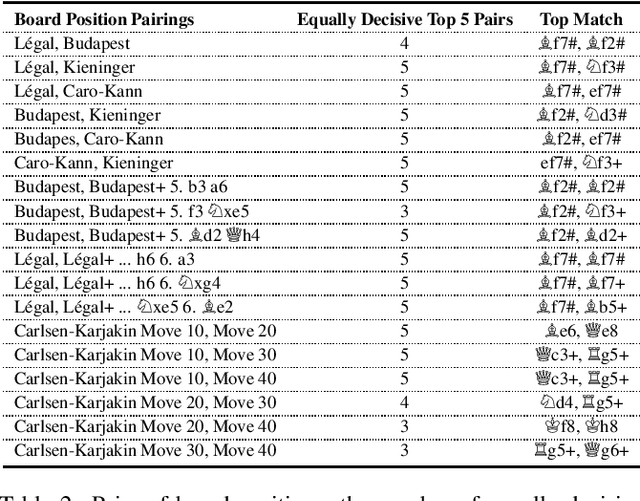
We study strategic similarity of game positions in two-player extensive games of perfect information, by looking at the structure of their local game trees, with the aim of improving the performance of game playing agents in detecting forcing continuations. We present a range of measures over the induced game trees and compare them against benchmark problems in chess, observing a promising level of accuracy in matching up trap states.

Computing rational decisions in extensive games with limited foresight

We introduce a class of extensive form games where players might not be able to foresee the possible consequences of their decisions and form a model of their opponents which they exploit to achieve a more profitable outcome. We improve upon existing models of games with limited foresight, endowing players with the ability of higher-order reasoning and proposing a novel solution concept to address intuitions coming from real game play. We analyse the resulting equilibria, devising an effective procedure to compute them.