Stanislav Zhydkov
Peer Selection with Noisy Assessments
Jul 21, 2021

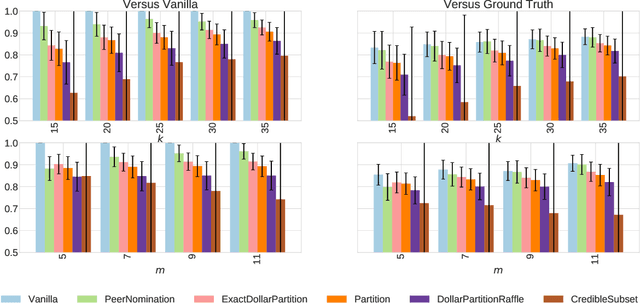
Abstract:In the peer selection problem a group of agents must select a subset of themselves as winners for, e.g., peer-reviewed grants or prizes. Here, we take a Condorcet view of this aggregation problem, i.e., that there is a ground-truth ordering over the agents and we wish to select the best set of agents, subject to the noisy assessments of the peers. Given this model, some agents may be unreliable, while others might be self-interested, attempting to influence the outcome in their favour. In this paper we extend PeerNomination, the most accurate peer reviewing algorithm to date, into WeightedPeerNomination, which is able to handle noisy and inaccurate agents. To do this, we explicitly formulate assessors' reliability weights in a way that does not violate strategyproofness, and use this information to reweight their scores. We show analytically that a weighting scheme can improve the overall accuracy of the selection significantly. Finally, we implement several instances of reweighting methods and show empirically that our methods are robust in the face of noisy assessments.
PeerNomination: Relaxing Exactness for Increased Accuracy in Peer Selection
Apr 30, 2020
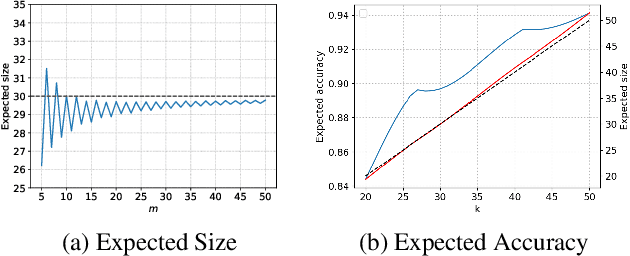
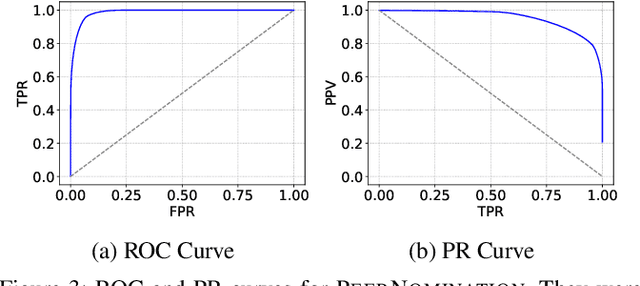
Abstract:In peer selection agents must choose a subset of themselves for an award or a prize. As agents are self-interested, we want to design algorithms that are impartial, so that an individual agent cannot affect their own chance of being selected. This problem has broad application in resource allocation and mechanism design and has received substantial attention in the artificial intelligence literature. Here, we present a novel algorithm for impartial peer selection, PeerNomination, and provide a theoretical analysis of its accuracy. Our algorithm possesses various desirable features. In particular, it does not require an explicit partitioning of the agents, as previous algorithms in the literature. We show empirically that it achieves higher accuracy than the exiting algorithms over several metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge