PeerNomination: Relaxing Exactness for Increased Accuracy in Peer Selection
Paper and Code
Apr 30, 2020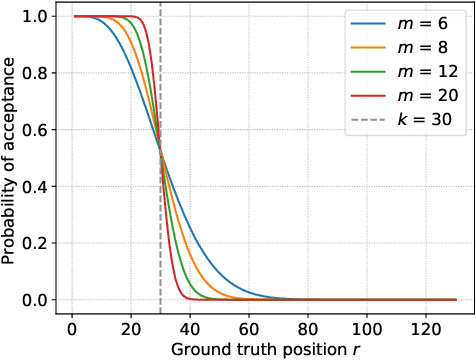
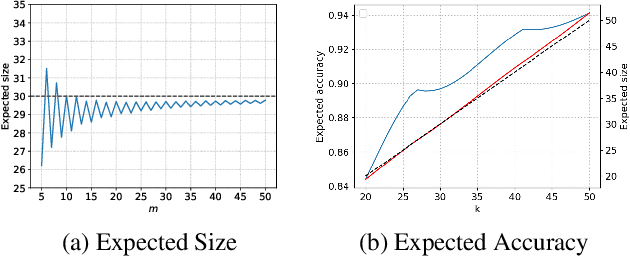
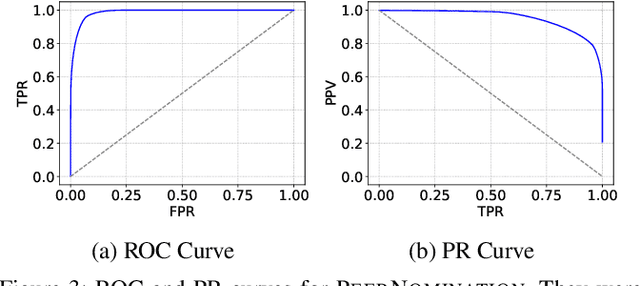
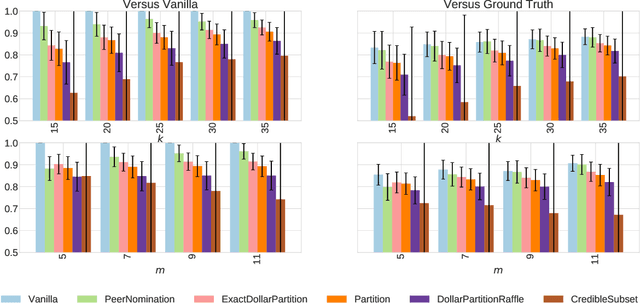
In peer selection agents must choose a subset of themselves for an award or a prize. As agents are self-interested, we want to design algorithms that are impartial, so that an individual agent cannot affect their own chance of being selected. This problem has broad application in resource allocation and mechanism design and has received substantial attention in the artificial intelligence literature. Here, we present a novel algorithm for impartial peer selection, PeerNomination, and provide a theoretical analysis of its accuracy. Our algorithm possesses various desirable features. In particular, it does not require an explicit partitioning of the agents, as previous algorithms in the literature. We show empirically that it achieves higher accuracy than the exiting algorithms over several metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge